Supernatural numbers also appear in noncommutative geometry via James Glimm’s characterisation of a class of simple $C^*$-algebras, the UHF-algebras.
A uniformly hyperfine (or, UHF) algebra $A$ is a $C^*$-algebra that can be written as the closure, in the norm topology, of an increasing union of finite-dimensional full matrix algebras
$M_{c_1}(\mathbb{C}) \subset M_{c_2}(\mathbb{C}) \subset … \quad \subset A$
Such embedding are only possible if the matrix-sizes divide each other, that is $c_1 | c_2 | c_3 | … $, and we can assign to $A$ the supernatural number $s=\prod_i c_i$ and denote $A=A(s)$.
In his paper On a certain class of operator algebras, Glimm proved that two UHF-algebras $A(s)$ and $B(t)$ are isomorphic as $C^*$-algebras if and only if $s=t$. That is, the supernatural numbers $\mathbb{S}$ are precisely the isomorphism classes of UHF-algebras.
An important invariant, the Grothendieck group $K_0$ of $A(s)$, can be described as the additive subgroup $\mathbb{Q}(s)$ of $\mathbb{Q}$ generated by all fractions of the form $\frac{1}{n}$ where $n$ is a positive integer dividing $s$.
A “noncommutative space” is a Morita class of $C^*$-algebras, so we want to know when two $UHF$-algebras $A(s)$ and $B(t)$ are Morita-equivalent. This turns out to be the case when there are positive integers $n$ and $m$ such that $n.s = m.t$, or equivalently when the $K_0$’s $\mathbb{Q}(s)$ and $\mathbb{Q}(t)$ are isomorphic as additive subgroups of $\mathbb{Q}$.
Thus Morita-equivalence defines an equivalence relation on $\mathbb{S}$ as follows: if $s=\prod p^{s_p}$ and $t= \prod p^{t_p}$ then $s \sim t$ if and only if the following two properties are satisfied:
(1): $s_p = \infty$ iff $t_p= \infty$, and
(2): $s_p=t_p$ for all but finitely many primes $p$.
That is, we can view the equivalence classes $\mathbb{S}/\sim$ as the moduli space of noncommutative spaces associated to UHF-algebras!
Now, the equivalence relation is described in terms of isomorphism classes of additive subgroups of the rationals, which was precisely the characterisation of isomorphism classes of points in the arithmetic site, that is, the finite adèle classes
$\mathbb{S}/\sim~\simeq~\mathbb{Q}^* \backslash \mathbb{A}^f_{\mathbb{Q}} / \widehat{\mathbb{Z}}^*$
and as the induced topology of $\mathbb{A}^f_{\mathbb{Q}}$ on it is trivial, this “space” is usually thought of as a noncommutative space.
That is, $\mathbb{S}/\sim$ is a noncommutative moduli space of noncommutative spaces defined by UHF-algebras.
The finite integers form one equivalence class, corresponding to the fact that the finite dimensional UHF-algebras $M_n(\mathbb{C})$ are all Morita-equivalent to $\mathbb{C}$, or a bit more pompous, that the Brauer group $Br(\mathbb{C})$ is trivial.
Multiplication of supernaturals induces a well defined multiplication on equivalence classes, and, with that multiplication we can view $\mathbb{S}/\sim$ as the ‘Brauer-monoid’ $Br_{\infty}(\mathbb{C})$ of simple UHF-algebras…
(Btw. the photo of James Glimm above was taken by George Bergman in 1972)
Comments closed A standard
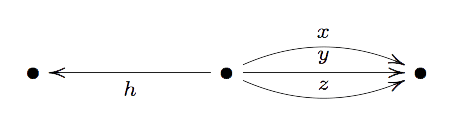
A standard 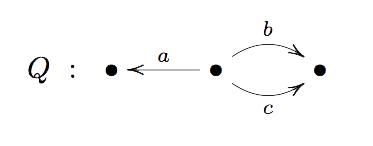
 Let’s illustrate the argument by finding a quiver Grassmannian $QGr(m,V)$ isomorphic to the
Let’s illustrate the argument by finding a quiver Grassmannian $QGr(m,V)$ isomorphic to the