Last time we’ve constructed a wide variety of Jaccard-like distance functions $d(m,n)$ on the set of all notes in our vault $V = \{ k,l,m,n,\dots \}$. That is, $d(m,n) \geq 0$ and for each triple of notes we have a triangle inequality
$$d(k,l)+d(l,m) \geq d(k,m)$$
By construction we had $d(m,n)=d(n,m)$, but we can modify any of these distances by setting $d'(m,n)= \infty$ if there is no path of internal links from note $m$ to note $n$, and $d'(m,n)=d(m,n)$ otherwise. This new generalised distance is no longer symmetric, but still satisfies the triangle inequality, and turns $V$ into a Lawvere space.
$V$ becomes an enriched category over the monoidal category $[0,\infty]=\mathbb{R}_+ \cup \{ \infty \}$ (the poset-category for the reverse ordering ($a \rightarrow b$ iff $a \geq b$) with $+$ as ‘tensor product’ and $0$ as unit). The ‘enrichment’ is the map
$$V \times V \rightarrow [0,\infty] \qquad (m,n) \mapsto d(m,n)$$
Writers (just like children) have always loved colimits. They want to morph their notes into a compelling story. Sadly, such colimits do not always exist yet in our vault category. They are among too many notes still missing from it.

(Image credit)
For ordinary categories, the way forward is to ‘upgrade’ your category to the presheaf category. In it, ‘the child can cobble together crazy constructions to his heart’s content’. For our ‘enriched’ vault $V_d$ we should look at the (enriched) category of enriched presheaves $\widehat{V_d}$. In it, the writer will find inspiration on how to cobble together her texts.
An enriched presheaf is a map $p : V \rightarrow [0,\infty]$ such that for all notes $m,n \in V$ we have
$$d(m,n) + p(n) \geq p(m)$$
Think of $p(n)$ as the distance (or similarity) of the virtual note $p$ to the existing note $n$, then this condition is just an extension of the triangle inequality. The lower the value of $p(n)$ the closer $p$ resembles $n$.
Each note $n \in V$ determines its Yoneda presheaf $y_n : V \rightarrow [0,\infty]$ by $m \mapsto d(m,n)$. By the triangle inequality this is indeed an enriched presheaf in $\widehat{V_d}$.
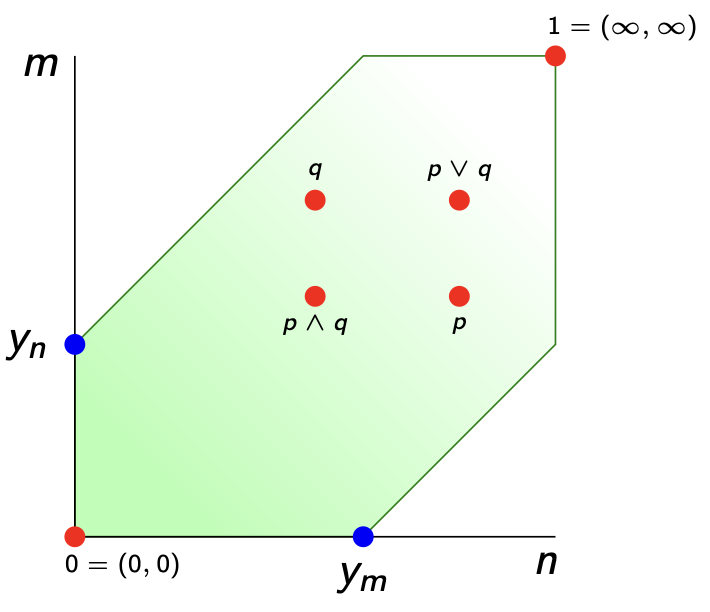
The set of all enriched presheaves $\widehat{V_d}$ has a lot of extra structure. It is a poset
$$p \leq q \qquad \text{iff} \qquad \forall n \in V : p(n) \leq q(n)$$
with minimal element $0 : \forall n \in V, 0(n)=0$, and maximal element $1 : \forall n \in V, 1(n)=\infty$.
It is even a lattice with $p \vee q(n) = max(p(n),q(n))$ and $p \wedge q(n)=min(p(n),q(n))$. It is easy to check that $p \wedge q$ and $p \vee q$ are again enriched presheaves.
Here’s $\widehat{V_d}$ when the vault consists of just two notes $V=\{ m,n \}$ of non-zero distance to each other (whether symmetric or not) as a subset of $[0,\infty] \times [0,\infty]$.
This vault $\widehat{V_d}$ of all missing (and existing) notes is again enriched over $[0,\infty]$ via
$$\widehat{d} : \widehat{V_d} \times \widehat{V_d} \rightarrow [0,\infty] \qquad \widehat{d}(p,q) = max(0,\underset{n \in V}{sup} (q(n)-p(n)))$$
The triangle inequality follows because the definition of $\widehat{d}(p,q)$ is equivalent to $\forall m \in V : \widehat{d}(p,q)+p(m) \geq q(m)$. Even if we start from a symmetric distance function $d$ on $V$, it is clear that this extended distance $\widehat{d}$ on $\widehat{V_d}$ is far from symmetric. The Yoneda map
$$y : V_d \rightarrow \widehat{V_d} \qquad n \mapsto y_n$$
is an isometry and the enriched version of the Yoneda lemma says that for all $p \in \widehat{V_d}$
$$p(n) = \widehat{d}(y_n,p)$$
Indeed, taking $m=n$ in $\widehat{d}(y_n,f)+y_n(m) \geq p(m)$ gives $\widehat{d}(y_n,p) \geq p(n)$. Conversely,
from the presheaf condition $d(m,n)+p(n) \geq p(m)$ for all $m,n$ follows
$$p(n) \geq max(0,\underset{m \in V}{sup}(p(m)-d(m,n)) = \widehat{d}(y_n,p)$$
In his paper Taking categories seriously, Bill Lawvere suggested to consider enriched presheaves $p \in \widehat{V_d}$ as ‘refined’ closed set of the vault-space $V_d$.
For every subset of notes $X \subset V$ we can consider the presheaf (use triangle inequality)
$$p_X : V \rightarrow [0,\infty] \qquad m \mapsto \underset{n \in X}{inf}~d(m,n)$$
then its zero set $Z(p_X) = \{ m \in V~:~p_X(m)=0 \}$ can be thought of as the closure of $X$, and the collection of all such closed subsets define a topology on $V$.
In our simple example of the two note vault $V=\{ m,n \}$ this is just the discrete topology, but we can get more interesting spaces. If $d(n,m)=0$ but $d(m,n) > 0$
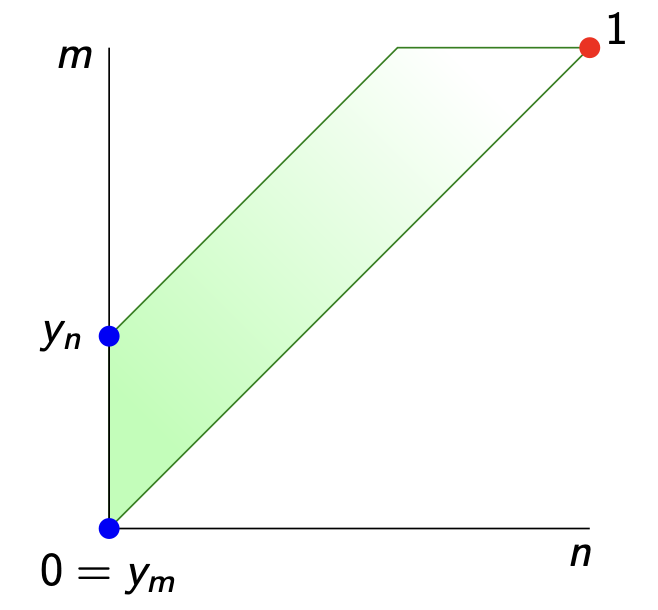
we get the Sierpinski space: $n$ is the only closed point, and lies in the closure of $m$. Of course, if your vault contains thousands of notes, you might get more interesting topologies.
In the special case when $V_d$ is a poset-category, as was the case in the shape of languages post, this topology is the down-set (or up-set) topology.
Now, what is this topology when you start with the Lawvere-space $\widehat{V_d}$? From the definitions we see that
$$\widehat{d}(p,q) = 0 \quad \text{iff} \quad \forall n \in V~:~p(n) \geq q(n) \quad \text{iff} \quad p \geq q$$
So, all presheaves in the up-set $\uparrow_p$ lie in the closure of $p$, and $p$ lies in the closure of all everything in the down-set $\downarrow_p$ of $p$. So, this time the topology has as its closed sets all down-sets of the poset $\widehat{V_d}$.
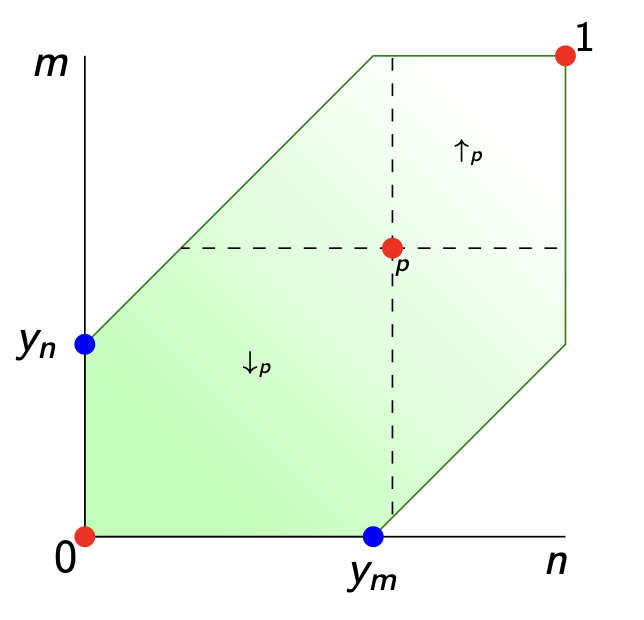
What’s missing is a good definition for the implication $p \Rightarrow q$ between two enriched presheaves $p,q \in \widehat{V_d}$. In An enriched category theory of language: from syntax to semantics it is said that this should be, perhaps only to be used in their special poset situation (with adapted notations)
$$p \Rightarrow q : V \rightarrow [0,\infty] \qquad \text{where} \quad (p \Rightarrow q)(n) = \widehat{d}(y_n \wedge p,q)$$
but I can’t even show that this is a presheaf. I may be horribly wrong, but in their proof of this (lemma 5) they seem to use their lemma 4, but with the two factors swapped.
If you have suggestions, please let me know. And if you trow Kelly’s Basic concepts of enriched category theory at me, please add some guidelines on how to use it. I’m just a passer-by.
Probably, I should also read up on Isbell duality, as suggested by Lawvere in his paper Taking categories seriously, and worked out by Simon Willerton in Tight spans, Isbell completions and semi-tropical modules…
(tbc)
Previously in this series:
Next
Comments closed