The enriched vault – neverendingbooks

In the shape of languages we started from a collection of notes, made a poset of text-snippets from them, and turned this into an enriched category over the unit interval $[0, 1]$ , following the paper paper An enriched category theory of language: from syntax to semantics by Tai-Danae Bradley, John Terilla and Yiannis Vlassopoulos.

This allowed us to view the text-snippets as points in a Lawvere pseudoquasi metric space, and to define a ‘topos’ of enriched presheaves on it, including the Yoneda-presheaves containing semantic information of the snippets.

In the previous post we looked at ‘building a second brain’ apps, such as LogSeq and Obsidian, and hoped to use them to test the conjectured ‘topos of the unconscious’.

In Obsidian, a vault is a collection of notes (with their tags and other meta-data), together with all links between them.

The vault of the language-poset will have one note for every text-snipped, and have a link from note $n$ to note $m$ if $m$ is a text-fragment in $n$ .

In their paper, Bradley, Terilla and Vlassopoulos use the enrichment structure where $μ (n, m) \in [0, 1]$ is the conditional probablity of the fragment $m$ to be extended to the larger text $n$ .

Most Obsidian vaults are a lot more complicated, possibly having oriented cycles in their internal link structure.

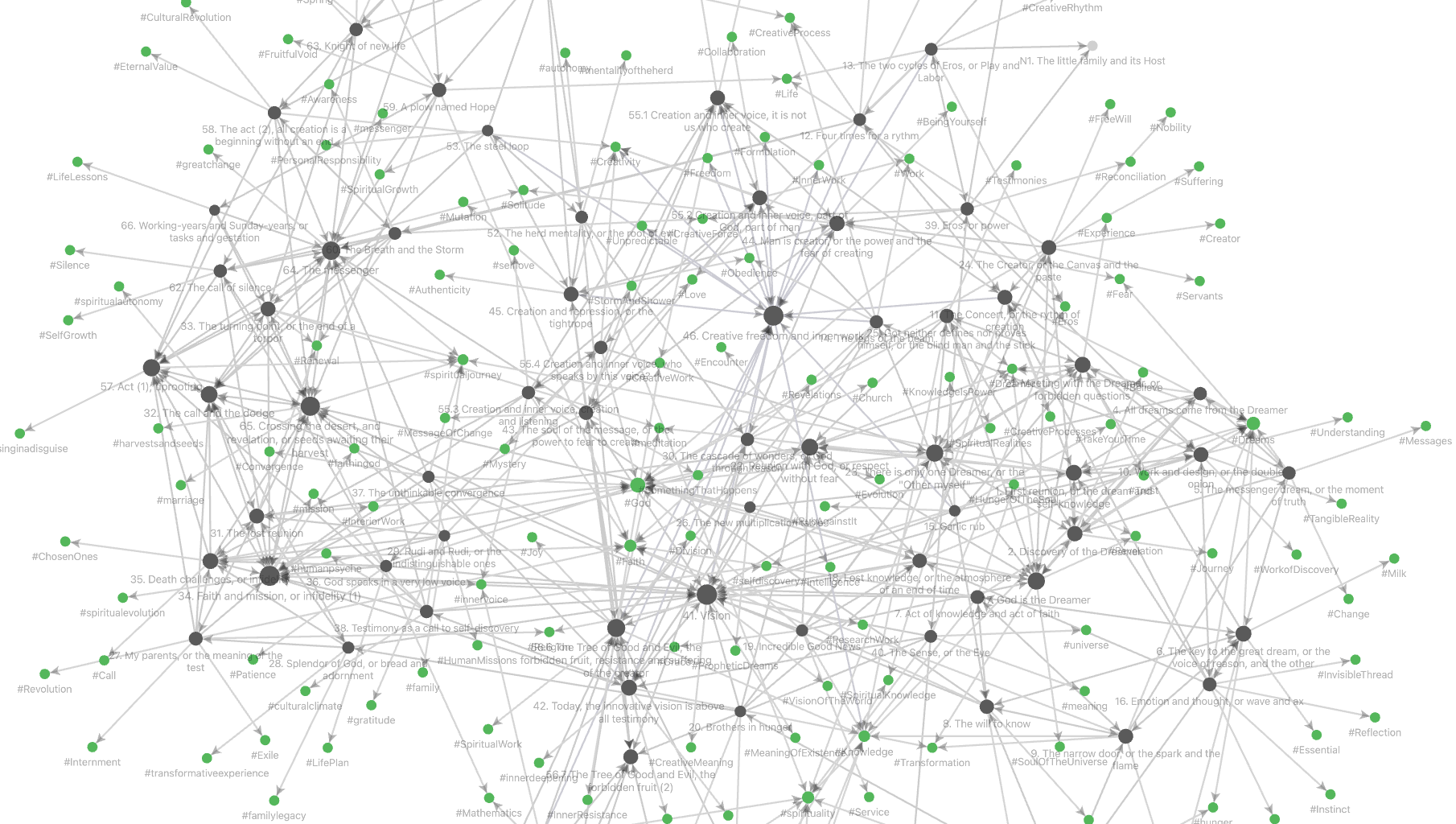
Still, it is always possible to turn the notes of the vault into a category enriched over $[0, 1]$ , in multiple ways, depending on whether we want to focus on the internal link-structure or rather on the semantic similarity between notes, or any combination of these.

Let $X$ be a set of searchable data from your vault. Elements of $X$ may be

words contained in notes
in- or out-going links between notes
tags used
YAML-frontmatter
…

Assign a positive real number $r_{x} \geq 0$ to every $x \in X$ . We see $r_{x}$ as the ‘relevance’ we attach to the search term $x$ . So, it is possible to emphasise certain key-words or tags, find certain links more important than others, and so on.

For this relevance function $r : X \to R_{+}$ , we have a function defined on all subsets $Y$ of $X$

$f_{r} : P (X) \to R_{+} Y \mapsto f_{r} (Y) = \sum_{x \in Y} r_{x}$

Take a note $n$ from the vault $V$ and let $X_{n}$ be the set of search terms from $X$ contained in $n$ .

We can then define a (generalised) Jaccard distance for any pair of notes $n$ and $m$ in $V$ :

$d_{r} (n, m) = {\begin{cases} 0 if f_{r} (X_{n} \cup X_{m}) = 0 \\ 1 - \frac{f_{r} (X_{n} \cap X_{m})}{f_{r} (X_{n} \cup X_{m})} otherwise \end{cases}$

This distance is symmetric, $d_{r} (n, n) = 0$ for all notes $n$ , and the crucial property is that it satisfies the triangle inequality, that is, for all triples of notes $l$ , $m$ and $n$ we have

$d_{r} (l, n) \leq d_{r} (l, m) + d_{r} (m, n)$

For a proof in this generality see the paper A note on the triangle inequality for the Jaccard distance by Sven Kosub.

How does this help to make the vault $V$ into a category enriched over $[0, 1]$ ?

The poset $([0, 1], \leq)$ is the category with objects all numbers $a \in [0, 1]$ , and a unique morphism $a \to b$ between two numbers iff $a \leq b$ . This category has limits (infs) and colimits (sups), has a monoidal structure $a \otimes b = a \times b$ with unit object $1$ , and an internal hom

$H o m_{[0, 1]} (a, b) = (a, b) = {\begin{cases} \frac{b}{a} if b \leq a \\ 1 otherwise \end{cases}$

We say that the vault is an enriched category over $[0, 1]$ if for every pair of notes $n$ and $m$ we have a number $μ (n, m) \in [0, 1]$ satisfying for all notes $n$

$μ (n, n) = 1 and μ (m, l) \times μ (n, m) \leq μ (n, l)$

for all triples of notes $l, m$ and $n$ .

Starting from any relevance function $r : X \to R_{+}$ we define for every pair $n$ and $m$ of notes the distance function $d_{r} (m, n)$ satisfying the triangle inequality. If we now take

$μ_{r} (m, n) = e^{- d_{r} (m, n)}$

then the triangle inequality translates for every triple of notes $l, m$ and $n$ into

$μ_{r} (m, l) \times μ_{r} (n, m) \leq μ_{r} (n, l)$

That is, every relevance function makes $V$ into a category enriched over $[0, 1]$ .

Two simple relevance functions, and their corresponding distance and enrichment functions are available from Obsidian’s Graph Analysis community plugin.

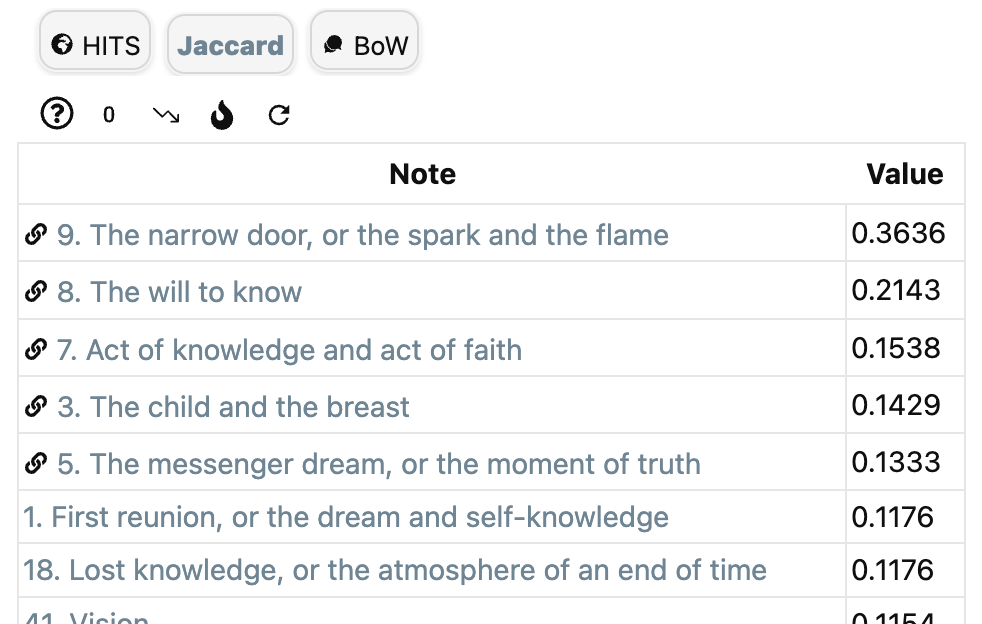
To get structural information on the link-structure take as $X$ the set of all incoming and outgoing links in your vault, with relevance function the constant function $1$ .

‘Jaccard’ in Graph Analysis computes for the current note $n$ the value of $1 - d_{r} (n, m)$ for all notes $m$ , so if this value is $a \in [0, 1]$ , then the corresponding enrichment value is $μ_{r} (m, n) = e^{a - 1}$ .

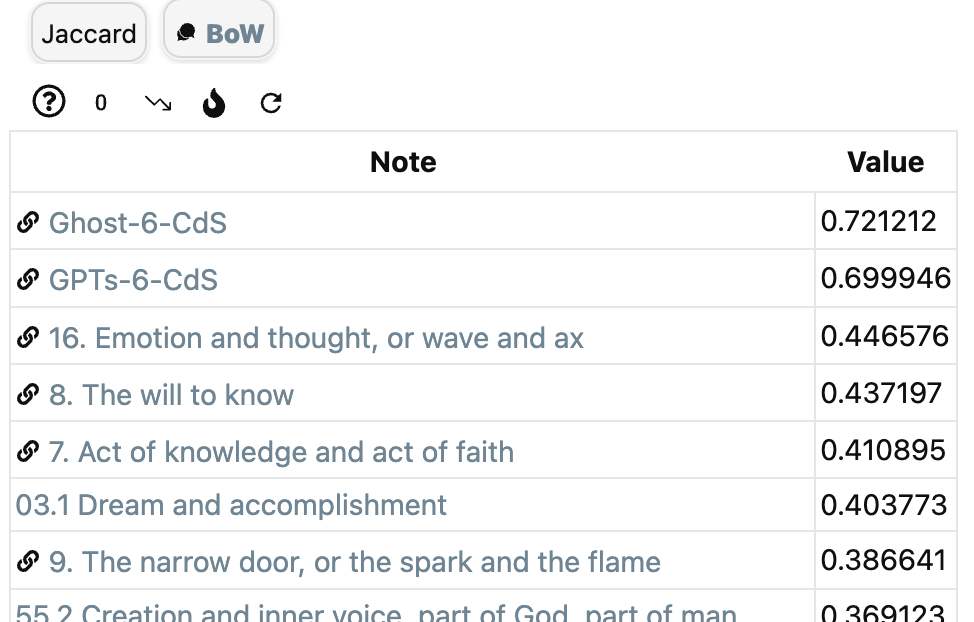
To get semantic information on the similarity between notes, let $X$ be the set of all words in all notes and take again as relevance function the constant function $1$ .

To access ‘BoW’ (Bags of Words) in Graph Analysis, you must first install the (non-community) NLP plugin which enables various types of natural language processing in the vault. The install is best done via the BRAT plugin (perhaps I’ll do a couple of posts on Obsidian someday).

If it gives for the current note $n$ the value $a$ for a note $m$ , then again we can take as the enrichment structure $μ_{r} (n, m) = e^{a - 1}$ .

Graph Analysis offers more functionality, and a good introduction is given in this clip:

Calculating the enrichment data for custom designed relevance functions takes a lot more work, but is doable. Perhaps I’ll return to this later.

Mathematically, it is probably more interesting to start with a given enrichment structure $μ$ on the vault $V$ , describe the category of all enriched presheaves $\hat{V_{μ}}$ and find out what we can do with it.

(tbc)

Previously in this series:

Next:

The super-vault of missing notes