Skip to content →

Tag: moonshine

the monstrous moonshine picture – 2

Published January 19, 2018 by lieven

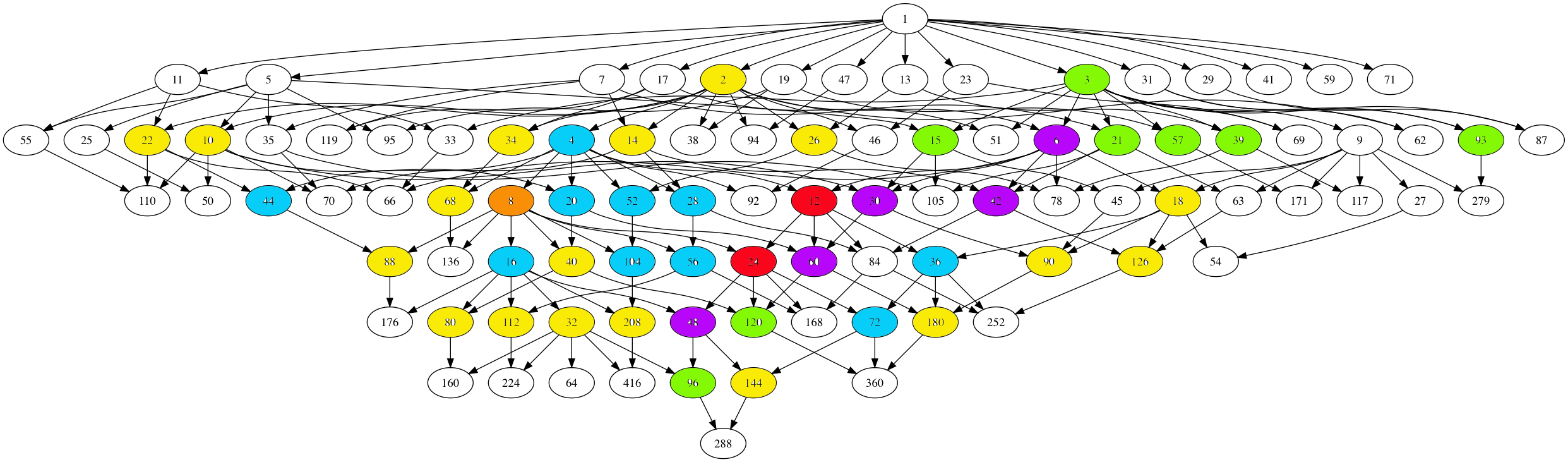
Time to wrap up my calculations on the moonshine picture, which is the subgraph of Conway’s Big Picture needed to describe all 171 moonshine groups.

No doubt I’ve made mistakes. All corrections are welcome. The starting point is the list of 171 moonshine groups which are in the original Monstrous Moonshine paper.

The backbone is given by the $97$ number lattices, which are closed under taking divisors and were found by looking at all divisors of the numbers $N=n \times h$ for the 171 moonshine groups of the form $N+e,f,\dots$ or $(n|h)+e,f,\dots$.

The Hasse-diagram of this poset (under division) is here (click on the image to get a larger version)

There are seven types of coloured numbers, each corresponding to number-lattices which have the same local structure in the moonshine picture, as in the previous post.

The white numbered lattices have no further edges in the picture.

The yellow number lattices (2,10,14,18,22,26,32,34,40,68,80,88,90,112,126,144,180,208 = 2M) have local structure

\[
\xymatrix{& \color{yellow}{2M} \ar@{-}[r] & M \frac{1}{2}} \]

The green number lattices (3,15,21,39,57,93,96,120 = 3M) have local structure

\[
\xymatrix{M \frac{1}{3} \ar@[red]@{-}[r] & \color{green}{3M} \ar@[red]@{-}[r] & M \frac{2}{3}} \]

The blue number lattices (4,16,20,28,36,44,52,56,72,104 = 4M) have as local structure

\[
\xymatrix{M \frac{1}{2} \ar@{-}[d] & & M \frac{1}{4} \ar@{-}[d] \\
2M \ar@{-}[r] & \color{blue}{4M} \ar@{-}[r] & 2M \frac{1}{2} \ar@{-}[d] \\
& & M \frac{3}{4}} \]

where the leftmost part is redundant as they are already included in the yellow-bit.

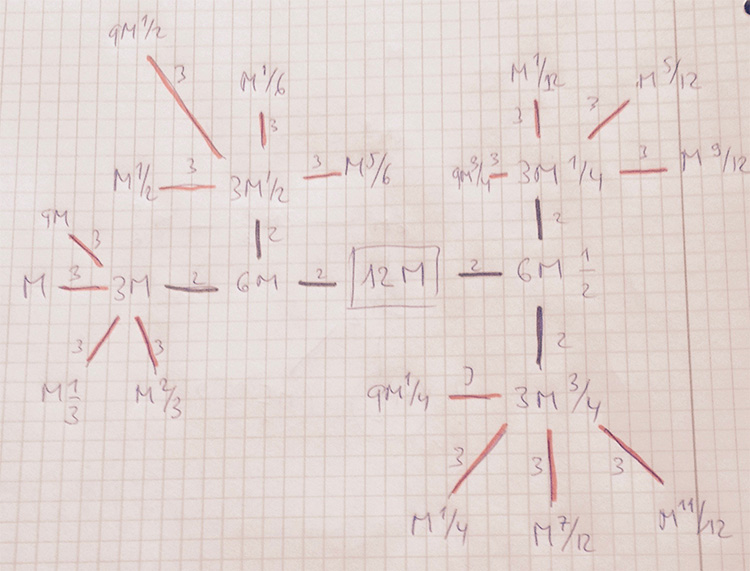
The purple number lattices (6,30,42,48,60 = 6M) have local structure

\[
\xymatrix{M \frac{1}{3} \ar@[red]@{-}[d] & 2M \frac{1}{3} & M \frac{1}{6} \ar@[red]@{-}[d] & \\
3M \ar@{-}[r] \ar@[red]@{-}[d] & \color{purple}{6M} \ar@{-}[r] \ar@[red]@{-}[u] \ar@[red]@{-}[d] & 3M \frac{1}{2} \ar@[red]@{-}[r] \ar@[red]@{-}[d] & M \frac{5}{6} \\
M \frac{2}{3} & 2M \frac{2}{3} & M \frac{1}{2} & } \]

where again the lefmost part is redundant, and I forgot to add the central part in the previous post… (updated now).

The unique brown number lattice 8 has local structure

\[
\xymatrix{& & 1 \frac{1}{4} \ar@{-}[d] & & 1 \frac{1}{8} \ar@{-}[d] & \\
& 1 \frac{1}{2} \ar@{-}[d] & 2 \frac{1}{2} \ar@{-}[r] \ar@{-}[d] & 1 \frac{3}{4} & 2 \frac{1}{4} \ar@{-}[r] & 1 \frac{5}{8} \\
1 \ar@{-}[r] & 2 \ar@{-}[r] & 4 \ar@{-}[r] & \color{brown}{8} \ar@{-}[r] & 4 \frac{1}{2} \ar@{-}[d] \ar@{-}[u] & \\
& & & 1 \frac{7}{8} \ar@{-}[r] & 2 \frac{3}{4} \ar@{-}[r] & 1 \frac{3}{8}} \]

The local structure in the two central red number lattices (not surprisingly 12 and 24) looks like the image in the previous post, but I have to add some ‘forgotten’ lattices.

That’ll have to wait…

Comments closed

Moonshine’s green anaconda

Published January 18, 2018 by lieven

The largest snake in the moonshine picture determines the moonshine group $(24|12)$ and is associated to conjugacy class $24J$ of the monster.

It contains $70$ lattices, about one third of the total number of lattices in the moonshine picture.

The anaconda’s backbone is the $(288|1)$ thread below (edges in the $2$-tree are black, those in the $3$-tree red and coloured numbers are symmetric with respect to the $(24|12)$-spine and have the same local snake-structure.

\[
\xymatrix{9 \ar@{-}[r] \ar@[red]@{-}[d] & \color{green}{18} \ar@{-}[r] \ar@[red]@{-}[d] & \color{yellow}{36} \ar@{-}[r] \ar@[red]@{-}[d] & \color{yellow}{72} \ar@{-}[r] \ar@[red]@{-}[d] & \color{green}{144} \ar@{-}[r] \ar@[red]@{-}[d] & 288 \ar@[red]@{-}[d] \\
3 \ar@{-}[r] \ar@[red]@{-}[d] & \color{blue}{6} \ar@{-}[r] \ar@[red]@{-}[d] & \color{red}{12} \ar@{-}[r] \ar@[red]@{-}[d] & \color{red}{24} \ar@{-}[r] \ar@[red]@{-}[d] & \color{blue}{48} \ar@{-}[r] \ar@[red]@{-}[d] & 96 \ar@[red]@{-}[d] \\
1 \ar@{-}[r] & \color{green}{2} \ar@{-}[r] & \color{yellow}{4} \ar@{-}[r] & \color{yellow}{8} \ar@{-}[r] & \color{green}{16} \ar@{-}[r] & 32 } \]

These are the only number-lattices in the anaconda. The remaining lattices are number-like, that is of the form $M \frac{g}{h}$ with $M$ an integer and $1 \leq g < h$ with $(g,h)=1$.
There are

– $12$ with $h=2$ and $M$ a divisor of $72$.

– $12$ with $h=3$ and $M$ a divisor of $32$.

– $12$ with $h=4$ and $M$ a divisor of $18$.

– $8$ with $h=6$ and $M$ a divisor of $8$.

– $8$ with $h=12$ and $M=1,2$.

The non-number lattices in the snake are locally in the coloured numbers:

In $2,16,18,144=2M$

\[
\xymatrix{& \color{green}{2M} \ar@{-}[r] & M \frac{1}{2}} \]

In $4,8,36,72=4M$

\[
\xymatrix{M \frac{1}{2} \ar@{-}[d] & & M \frac{1}{4} \ar@{-}[d] \\
2M \ar@{-}[r] & \color{yellow}{4M} \ar@{-}[r] & 2M \frac{1}{2} \ar@{-}[d] \\
& & M \frac{3}{4}} \]

In $6,48=6M$

\[
\xymatrix{M \frac{1}{3} \ar@[red]@{-}[d] & 2M \frac{1}{3} & M \frac{1}{6} \ar@[red]@{-}[d] & \\
3M \ar@{-}[r] \ar@[red]@{-}[d] & \color{blue}{6M} \ar@{-}[r] \ar@[red]@{-}[u] \ar@[red]@{-}[d] & 3M \frac{1}{2} \ar@[red]@{-}[r] \ar@[red]@{-}[d] & M \frac{5}{6} \\
M \frac{2}{3} & 2M \frac{2}{3} & M \frac{1}{2} & } \]

In $12,24=12M$ the local structure looks like

Here, we used the commutation relations to reach all lattices at distance $log(6)$ and $log(12)$ by first walking the $2$-adic tree and postpone the last step for the $3$-tree.

Perhaps this is also a good strategy to get a grip on the full moonshine picture:

First determine subsets of the moonshine thread with the same local structure, and then determine for each class this local structure.

Comments closed

the 171 moonshine groups

Published January 6, 2018 by lieven

Monstrous moonshine associates to every element of order $n$ of the monster group $\mathbb{M}$ an arithmetic group of the form
\[
(n|h)+e,f,\dots \]
where $h$ is a divisor of $24$ and of $n$ and where $e,f,\dots$ are divisors of $\frac{n}{h}$ coprime with its quotient.

In snakes, spines, and all that we’ve constructed the arithmetic group
\[
\Gamma_0(n|h)+e,f,\dots \]
which normalizes $\Gamma_0(N)$ for $N=h.n$. If $h=1$ then this group is the moonshine group $(n|h)+e,f,\dots$, but for $h > 1$ the moonshine group is a specific subgroup of index $h$ in $\Gamma_0(n|h)+e,f,\dots$.

I’m sure one can describe this subgroup explicitly in each case by analysing the action of the finite group $(\Gamma_0(n|h)+e,f,\dots)/\Gamma_0(N)$ on the $(N|1)$-snake. Some examples were worked out by John Duncan in his paper Arithmetic groups and the affine E8 Dynkin diagram.

But at the moment I don’t understand the general construction given by Conway, McKay and Sebbar in On the discrete groups of moonshine. I’m stuck at the last sentence of (2) in section 3. Nothing a copy of Charles Ferenbaugh Ph. D. thesis cannot fix.

The correspondence between the conjugacy classes of the Monster and these arithmetic groups takes up 3 pages in Conway & Norton’s Monstrous Moonshine. Here’s the beginning of it.

Comments closed