Moonshine’s green anaconda

The largest snake in the moonshine picture determines the moonshine group $(24|12)$ and is associated to conjugacy class $24J$ of the monster.

It contains $70$ lattices, about one third of the total number of lattices in the moonshine picture.

The anaconda’s backbone is the $(288|1)$ thread below (edges in the $2$-tree are black, those in the $3$-tree red and coloured numbers are symmetric with respect to the $(24|12)$-spine and have the same local snake-structure.

These are the only number-lattices in the anaconda. The remaining lattices are number-like, that is of the form $M\frac{g}{h}$ with $M$ an integer and $1\le g<h$ with $(g,h)=1$.
There are

– $12$ with $h=2$ and $M$ a divisor of $72$.

– $12$ with $h=3$ and $M$ a divisor of $32$.

– $12$ with $h=4$ and $M$ a divisor of $18$.

– $8$ with $h=6$ and $M$ a divisor of $8$.

– $8$ with $h=12$ and $M=1,2$.

The non-number lattices in the snake are locally in the coloured numbers:

In $2,16,18,144=2M$

In $4,8,36,72=4M$

In $6,48=6M$

In $12,24=12M$ the local structure looks like

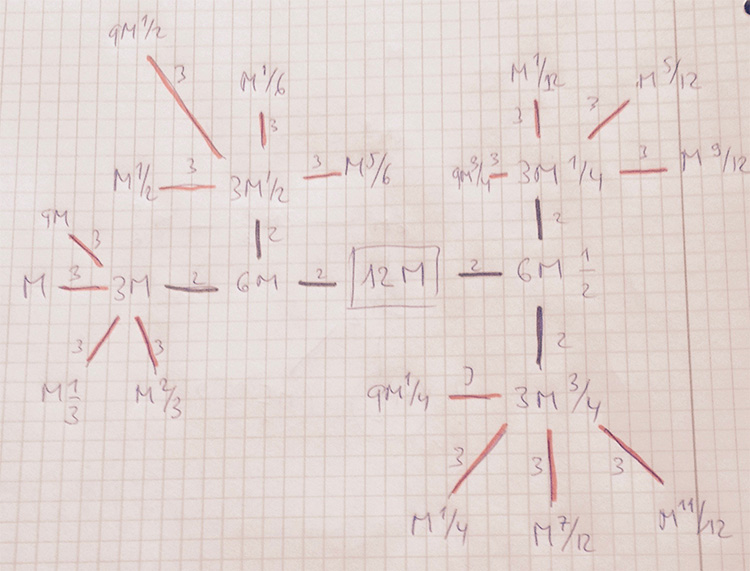
Here, we used the commutation relations to reach all lattices at distance $log(6)$ and $log(12)$ by first walking the $2$-adic tree and postpone the last step for the $3$-tree.

Perhaps this is also a good strategy to get a grip on the full moonshine picture:

First determine subsets of the moonshine thread with the same local structure, and then determine for each class this local structure.