Skip to content →

neverendingbooks Posts

a non-commutative Jack Daniels problem

Published January 20, 2018 by lieven

At a seminar at the College de France in 1975, Tits wrote down the order of the monster group

\[
\# \mathbb{M} = 2^{46}.3^{20}.5^9.7^6.11^2.13^3.17·19·23·29·31·41·47·59·71 \]

Andrew Ogg, who attended the talk, noticed that the prime divisors are precisely the primes $p$ for which the characteristic $p$ super-singular $j$-invariants are all defined over $\mathbb{F}_p$.

Here’s Ogg’s paper on this: Automorphismes de courbes modulaires, Séminaire Delange-Pisot-Poitou. Théorie des nombres, tome 16, no 1 (1974-1975).

Ogg offered a bottle of Jack Daniels for an explanation of this coincidence.

Even Richard Borcherds didn’t claim the bottle of Jack Daniels, though his proof of the monstrous moonshine conjecture is believed to be the best explanation, at present.

A few years ago, John Duncan and Ken Ono posted a paper “The Jack Daniels Problem”, in which they prove that monstrous moonshine implies that if $p$ is not one of Ogg’s primes it cannot be a divisor of $\# \mathbb{M}$. However, the other implication remains mysterious.

Duncan and Ono say:

“This discussion does not prove that every $p ∈ \text{Ogg}$ divides $\# \mathbb{M}$. It merely explains how the first principles of moonshine suggest this implication. Monstrous moonshine is the proof. Does this then provide a completely satisfactory solution to Ogg’s problem? Maybe or maybe not. Perhaps someone will one day furnish a map from the characteristic $p$ supersingular $j$-invariants to elements of order $p$ where the group structure of $\mathbb{M}$ is apparent.”

I don’t know whether they claimed the bottle, anyway.

But then, what is the non-commutative Jack Daniels Problem?

A footnote on the first page of Conway and Norton’s ‘Monstrous Moonshine’ paper says:

“Very recently, A. Pizer has shown these primes are the only ones that satisfy a certain conjecture of Hecke from 1936 relating modular forms of weight $2$ to quaternion algebra theta-series.”

Pizer’s paper is “A note on a conjecture of Hecke”.

Maybe there’s a connection between monstrous moonshine and the arithmetic of integral quaternion algebras. Some hints:

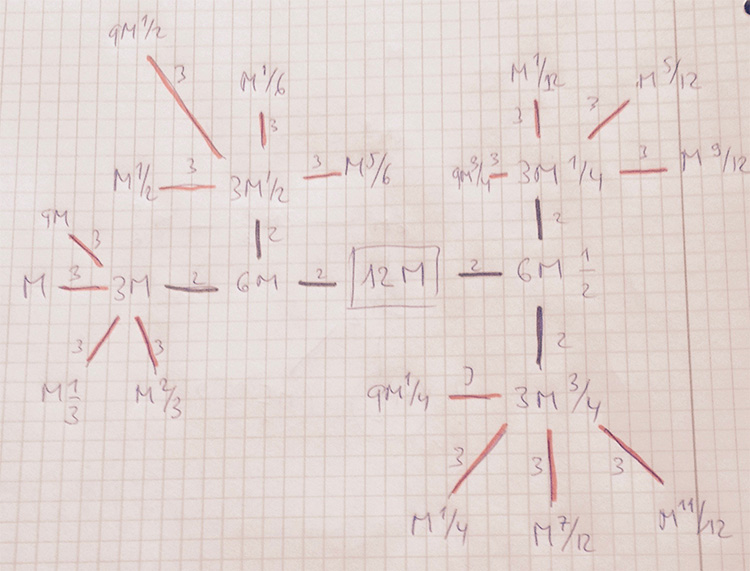
The commutation relations in the Big Picture are reminiscent of the meta-commutation relations for Hurwitz quaternions, originally due to Conway in his booklet on Quaternions and Octonions.

The fact that the $p$-tree in the Big Picture has valency $p+1$ comes from the fact that the Brauer-Severi of $M_2(\mathbb{F}_p)$ is $\mathbb{P}^1_{\mathbb{F}_p}$. In fact, the Big Picture should be related to the Brauer-Severi scheme of $M_2(\mathbb{Z})$.

Then, there’s Jorge Plazas claiming that Connes-Marcolli’s $GL_2$-system might be related to moonshine.

One of the first things I’ll do when I return is to run to the library and get our copy of Shimura’s ‘Introduction to the arithmetic theory of automorphic functions’.

Btw. the bottle in the title image is not a Jack Daniels but the remains of a bottle of Ricard, because I’m still in the French mountains.

Comments closed

the monstrous moonshine picture – 2

Published January 19, 2018 by lieven

Time to wrap up my calculations on the moonshine picture, which is the subgraph of Conway’s Big Picture needed to describe all 171 moonshine groups.

No doubt I’ve made mistakes. All corrections are welcome. The starting point is the list of 171 moonshine groups which are in the original Monstrous Moonshine paper.

The backbone is given by the $97$ number lattices, which are closed under taking divisors and were found by looking at all divisors of the numbers $N=n \times h$ for the 171 moonshine groups of the form $N+e,f,\dots$ or $(n|h)+e,f,\dots$.

The Hasse-diagram of this poset (under division) is here (click on the image to get a larger version)

There are seven types of coloured numbers, each corresponding to number-lattices which have the same local structure in the moonshine picture, as in the previous post.

The white numbered lattices have no further edges in the picture.

The yellow number lattices (2,10,14,18,22,26,32,34,40,68,80,88,90,112,126,144,180,208 = 2M) have local structure

\[
\xymatrix{& \color{yellow}{2M} \ar@{-}[r] & M \frac{1}{2}} \]

The green number lattices (3,15,21,39,57,93,96,120 = 3M) have local structure

\[
\xymatrix{M \frac{1}{3} \ar@[red]@{-}[r] & \color{green}{3M} \ar@[red]@{-}[r] & M \frac{2}{3}} \]

The blue number lattices (4,16,20,28,36,44,52,56,72,104 = 4M) have as local structure

\[
\xymatrix{M \frac{1}{2} \ar@{-}[d] & & M \frac{1}{4} \ar@{-}[d] \\
2M \ar@{-}[r] & \color{blue}{4M} \ar@{-}[r] & 2M \frac{1}{2} \ar@{-}[d] \\
& & M \frac{3}{4}} \]

where the leftmost part is redundant as they are already included in the yellow-bit.

The purple number lattices (6,30,42,48,60 = 6M) have local structure

\[
\xymatrix{M \frac{1}{3} \ar@[red]@{-}[d] & 2M \frac{1}{3} & M \frac{1}{6} \ar@[red]@{-}[d] & \\
3M \ar@{-}[r] \ar@[red]@{-}[d] & \color{purple}{6M} \ar@{-}[r] \ar@[red]@{-}[u] \ar@[red]@{-}[d] & 3M \frac{1}{2} \ar@[red]@{-}[r] \ar@[red]@{-}[d] & M \frac{5}{6} \\
M \frac{2}{3} & 2M \frac{2}{3} & M \frac{1}{2} & } \]

where again the lefmost part is redundant, and I forgot to add the central part in the previous post… (updated now).

The unique brown number lattice 8 has local structure

\[
\xymatrix{& & 1 \frac{1}{4} \ar@{-}[d] & & 1 \frac{1}{8} \ar@{-}[d] & \\
& 1 \frac{1}{2} \ar@{-}[d] & 2 \frac{1}{2} \ar@{-}[r] \ar@{-}[d] & 1 \frac{3}{4} & 2 \frac{1}{4} \ar@{-}[r] & 1 \frac{5}{8} \\
1 \ar@{-}[r] & 2 \ar@{-}[r] & 4 \ar@{-}[r] & \color{brown}{8} \ar@{-}[r] & 4 \frac{1}{2} \ar@{-}[d] \ar@{-}[u] & \\
& & & 1 \frac{7}{8} \ar@{-}[r] & 2 \frac{3}{4} \ar@{-}[r] & 1 \frac{3}{8}} \]

The local structure in the two central red number lattices (not surprisingly 12 and 24) looks like the image in the previous post, but I have to add some ‘forgotten’ lattices.

That’ll have to wait…

Comments closed

Moonshine’s green anaconda

Published January 18, 2018 by lieven

The largest snake in the moonshine picture determines the moonshine group $(24|12)$ and is associated to conjugacy class $24J$ of the monster.

It contains $70$ lattices, about one third of the total number of lattices in the moonshine picture.

The anaconda’s backbone is the $(288|1)$ thread below (edges in the $2$-tree are black, those in the $3$-tree red and coloured numbers are symmetric with respect to the $(24|12)$-spine and have the same local snake-structure.

\[
\xymatrix{9 \ar@{-}[r] \ar@[red]@{-}[d] & \color{green}{18} \ar@{-}[r] \ar@[red]@{-}[d] & \color{yellow}{36} \ar@{-}[r] \ar@[red]@{-}[d] & \color{yellow}{72} \ar@{-}[r] \ar@[red]@{-}[d] & \color{green}{144} \ar@{-}[r] \ar@[red]@{-}[d] & 288 \ar@[red]@{-}[d] \\
3 \ar@{-}[r] \ar@[red]@{-}[d] & \color{blue}{6} \ar@{-}[r] \ar@[red]@{-}[d] & \color{red}{12} \ar@{-}[r] \ar@[red]@{-}[d] & \color{red}{24} \ar@{-}[r] \ar@[red]@{-}[d] & \color{blue}{48} \ar@{-}[r] \ar@[red]@{-}[d] & 96 \ar@[red]@{-}[d] \\
1 \ar@{-}[r] & \color{green}{2} \ar@{-}[r] & \color{yellow}{4} \ar@{-}[r] & \color{yellow}{8} \ar@{-}[r] & \color{green}{16} \ar@{-}[r] & 32 } \]

These are the only number-lattices in the anaconda. The remaining lattices are number-like, that is of the form $M \frac{g}{h}$ with $M$ an integer and $1 \leq g < h$ with $(g,h)=1$.
There are

– $12$ with $h=2$ and $M$ a divisor of $72$.

– $12$ with $h=3$ and $M$ a divisor of $32$.

– $12$ with $h=4$ and $M$ a divisor of $18$.

– $8$ with $h=6$ and $M$ a divisor of $8$.

– $8$ with $h=12$ and $M=1,2$.

The non-number lattices in the snake are locally in the coloured numbers:

In $2,16,18,144=2M$

\[
\xymatrix{& \color{green}{2M} \ar@{-}[r] & M \frac{1}{2}} \]

In $4,8,36,72=4M$

\[
\xymatrix{M \frac{1}{2} \ar@{-}[d] & & M \frac{1}{4} \ar@{-}[d] \\
2M \ar@{-}[r] & \color{yellow}{4M} \ar@{-}[r] & 2M \frac{1}{2} \ar@{-}[d] \\
& & M \frac{3}{4}} \]

In $6,48=6M$

\[
\xymatrix{M \frac{1}{3} \ar@[red]@{-}[d] & 2M \frac{1}{3} & M \frac{1}{6} \ar@[red]@{-}[d] & \\
3M \ar@{-}[r] \ar@[red]@{-}[d] & \color{blue}{6M} \ar@{-}[r] \ar@[red]@{-}[u] \ar@[red]@{-}[d] & 3M \frac{1}{2} \ar@[red]@{-}[r] \ar@[red]@{-}[d] & M \frac{5}{6} \\
M \frac{2}{3} & 2M \frac{2}{3} & M \frac{1}{2} & } \]

In $12,24=12M$ the local structure looks like

Here, we used the commutation relations to reach all lattices at distance $log(6)$ and $log(12)$ by first walking the $2$-adic tree and postpone the last step for the $3$-tree.

Perhaps this is also a good strategy to get a grip on the full moonshine picture:

First determine subsets of the moonshine thread with the same local structure, and then determine for each class this local structure.

Comments closed