Judging from this and that paper, deep learning is the string theory of the 2020s for geometers and representation theorists.
String theory is the 90s answer to the tears of algebraic geometers worldwide trying to write the "Applications" part of their grant proposals. https://t.co/AboZ5WkPtc
— algebraic geometer BLM (@BarbaraFantechi) December 17, 2021
If you want to know quickly what neural networks really are, I can recommend the post demystifying deep learning.
The typical layout of a deep neural network has an input layer $L_0$ allowing you to feed $N_0$ numbers to the system (a vector $\vec{v_0} \in \mathbb{R}^{N_0}$), an output layer $L_p$ spitting $N_p$ numbers back (a vector $\vec{v_p} \in \mathbb{R}^{N_p}$), and $p-1$ hidden layers $L_1,\dots,L_{p-1}$ where all the magic happens. The hidden layer $L_i$ has $N_i$ virtual neurons, their states giving a vector $\vec{v_i} \in \mathbb{R}^{N_i}$.
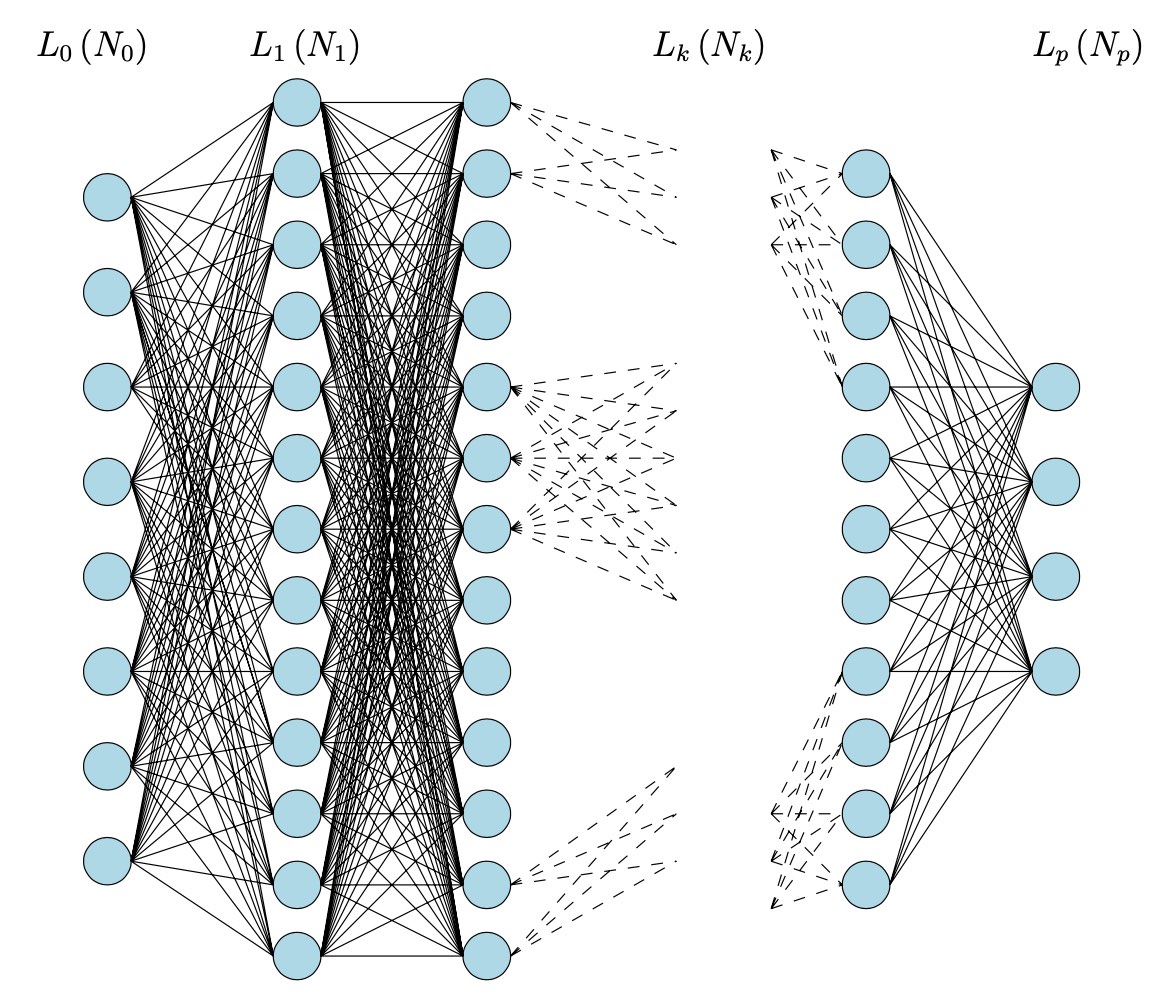
Picture taken from Logical informations cells I
For simplicity let’s assume all neurons in layer $L_i$ are wired to every neuron in layer $L_{i+1}$, the relevance of these connections given by a matrix of weights $W_i \in M_{N_{i+1} \times N_i}(\mathbb{R})$.
If at any given moment the ‘state’ of the neural network is described by the state-vectors $\vec{v_1},\dots,\vec{v_{p-1}}$ and the weight-matrices $W_0,\dots,W_p$, then an input $\vec{v_0}$ will typically result in new states of the neurons in layer $L_1$ given by
\[
\vec{v_1}’ = c_0(W_0.\vec{v_0}+\vec{v_1}) \]
which will then give new states in layer $L_2$
\[
\vec{v_2}’ = c_1(W_1.\vec{v_1}’+\vec{v_2}) \]
and so on, rippling through the network, until we get as the output
\[
\vec{v_p} = c_{p-1}(W_{p-1}.\vec{v_{p-1}}’) \]
where all the $c_i$ are fixed smooth activation functions $c_i : \mathbb{R}^{N_{i+1}} \rightarrow \mathbb{R}^{N_{i+1}}$.
This is just the dynamic, or forward working of the network.
The learning happens by comparing the computed output with the expected output, and working backwards through the network to alter slightly the state-vectors in all layers, and the weight-matrices between them. This process is called back-propagation, and involves the gradient descent procedure.
Even from this (over)simplified picture it seems doubtful that set valued (!) toposes are suitable to describe deep neural networks, as the Paris-Huawei-topos-team claims in their recent paper Topos and Stacks of Deep Neural Networks.
Still, there is a vast generalisation of neural networks: learners, developed by Brendan Fong, David Spivak and Remy Tuyeras in their paper Backprop as Functor: A compositional perspective on supervised learning (which btw is an excellent introduction for mathematicians to neural networks).
For any two sets $A$ and $B$, a learner $A \rightarrow B$ is a tuple $(P,I,U,R)$ where
- $P$ is a set, a parameter space of some functions from $A$ to $B$.
- $I$ is the interpretation map $I : P \times A \rightarrow B$ describing the functions in $P$.
- $U$ is the update map $U : P \times A \times B \rightarrow P$, part of the learning procedure. The idea is that $U(p,a,b)$ is a map which sends $a$ closer to $b$ than the map $p$ did.
- $R$ is the request map $R : P \times A \times B \rightarrow A$, the other part of the learning procedure. The idea is that the new element $R(p,a,b)=a’$ in $A$ is such that $p(a’)$ will be closer to $b$ than $p(a)$ was.
The request map is also crucial is defining the composition of two learners $A \rightarrow B$ and $B \rightarrow C$. $\mathbf{Learn}$ is the (symmetric, monoidal) category with objects all sets and morphisms equivalence classes of learners (defined in the natural way).
In this way we can view a deep neural network with $p$ layers as before to be the composition of $p$ learners
\[
\mathbb{R}^{N_0} \rightarrow \mathbb{R}^{N_1} \rightarrow \mathbb{R}^{N_2} \rightarrow \dots \rightarrow \mathbb{R}^{N_p} \]
where the learner describing the transition from the $i$-th to the $i+1$-th layer is given by the equivalence class of data $(A_i,B_i,P_i,I_i,U_i,R_i)$ with
\[
A_i = \mathbb{R}^{N_i},~B_i = \mathbb{R}^{N_{i+1}},~P_i = M_{N_{i+1} \times N_i}(\mathbb{R}) \times \mathbb{R}^{N_{i+1}} \]
and interpretation map for $p = (W_i,\vec{v}_{i+1}) \in P_i$
\[
I_i(p,\vec{v_i}) = c_i(W_i.\vec{v_i}+\vec{v}_{i+1}) \]
The update and request maps (encoding back-propagation and gradient-descent in this case) are explicitly given in theorem III.2 of the paper, and they behave functorial (whence the title of the paper).
More generally, we will now associate objects of a topos (actually just sheaves over a simple topological space) to a network op $p$ learners
\[
A_0 \rightarrow A_1 \rightarrow A_2 \rightarrow \dots \rightarrow A_p \]
inspired by section I.2 of Topos and Stacks of Deep Neural Networks.
The underlying category will be the poset-category (the opposite of the ordering of the layers)
\[
0 \leftarrow 1 \leftarrow 2 \leftarrow \dots \leftarrow p \]
The presheaf on a poset is a locale and in this case even the topos of sheaves on the topological space with $p+1$ nested open sets.
\[
X = U_0 \supseteq U_1 \supseteq U_2 \supseteq \dots \supseteq U_p = \emptyset \]
If the learner $A_i \rightarrow A_{i+1}$ is (the equivalence class) of the tuple $(A_i,A_{i+1},P_i,I_i,U_i,R_i)$ we will now describe two sheaves $\mathcal{W}$ and $\mathcal{X}$ on the topological space $X$.
$\mathcal{W}$ has as sections $\Gamma(\mathcal{W},U_i) = \prod_{j=i}^{p-1} P_i$ and the obvious projection maps as the restriction maps.
$\mathcal{X}$ has as sections $\Gamma(\mathcal{X},U_i) = A_i \times \Gamma(\mathcal{W},U_i)$ and restriction map to the next smaller open
\[
\rho^i_{i+1}~:~\Gamma(\mathcal{X},U_i) \rightarrow \Gamma(\mathcal{X},U_{i+1}) \qquad (a_i,(p_i,p’)) \mapsto (p_i(a_i),p’) \]
and other retriction maps by composition.
A major result in Topos and Stacks of Deep Neural Networks is that back-propagation is a natural transformation, that is, a sheaf-morphism $\mathcal{X} \rightarrow \mathcal{X}$.
In this general setting of layered learners we can always define a map on the sections of $\mathcal{X}$ (for every open $U_i$), $\Gamma(\mathcal{X},U_i) \rightarrow \Gamma(\mathcal{X},U_i)$
\[
(a_,(p_i,p’)) \mapsto (R(p_i,a_i,p_i(a_i)),(U(p_i,a_i,p_i(a_i)),p’) \]
But, in order for this to define a sheaf-morphism, compatible with the restrictions, we will have to impose restrictions on the update and restriction maps of the learners, in general.
Still, in the special case of deep neural networks, this compatibility follows from the functoriality property of Backprop as Functor: A compositional perspective on supervised learning.
To be continued.
One Comment