Two lattices $L$ and $L’$ in the same vector space are called neighbours if their intersection $L \cap L’$ is of index two in both $L$ and $L’$.
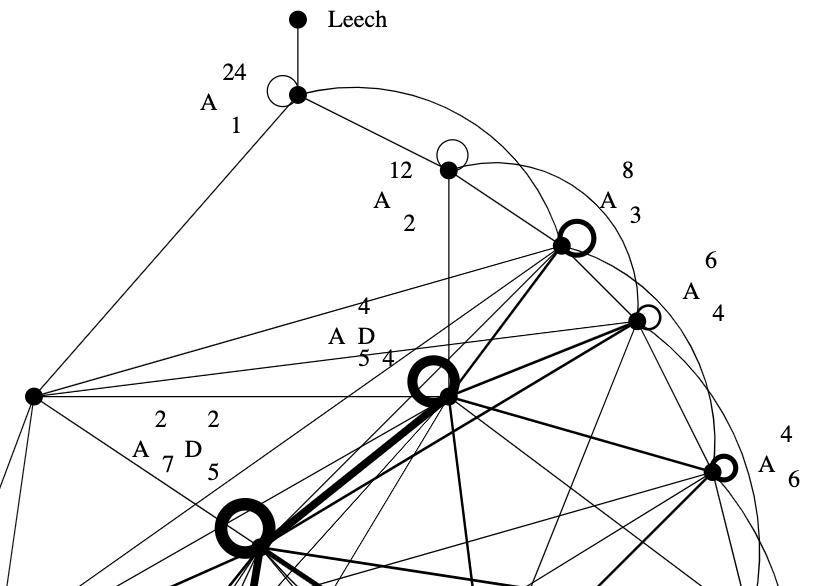
In 1957, Martin Kneser gave a method to find all unimodular lattices (of the same dimension and signature) starting from one such unimodular lattice, finding all its neighbours, and repeating this with the new lattices obtained.
In other words, Kneser’s neighbourhood graph, with vertices the unimodular lattices (of fixed dimension and signature) and edges between them whenever the lattices are neighbours, is connected.
Martin Kneser (1928-2004) – Photo Credit
Last time, we’ve constructed the Niemeier lattice $(A_1^{24})^+$ from the binary Golay code $\mathcal{C}_{24}$
\[
L = (A_1^{24})^+ = \mathcal{C}_{24} \underset{\mathbb{F}_2}{\times} (A_1^{24})^* = \{ \tfrac{1}{\sqrt{2}} \vec{v} ~|~\vec{v} \in \mathbb{Z}^{\oplus 24},~v=\vec{v}~mod~2 \in \mathcal{C}_{24} \} \]
With hindsight, we know that $(A_1^{24})^+$ is the unique neighbour of the Leech lattice in the Kneser neighbourhood graph of the positive definite, even unimodular $24$-dimensional lattices, aka the Niemeier lattices.
Let’s try to construct the Leech lattice $\Lambda$ from $L=(A_1^{24})^+$ by Kneser’s neighbour-finding trick.
Sublattices of $L$ of index two are in one-to-one correspondence with non-zero elements in $L/2L$. Take $l \in L – 2L$ and $m \in L$ such that the inner product $l.m$ is odd, then
\[
L_l = \{ x \in L~|~l.x~\text{is even} \} \]
is an index two sublattice because $L = L_l \sqcup (L_l+m)$. By definition $l.x$ is even for all $x \in L_l$ and therefore $\frac{l}{2} \in L_l^*$. We have this situation
\[
L_l \subsetneq L = L^* \subsetneq L_l^* \]
and $L_l^*/L_l \simeq \mathbb{F}_2 \oplus \mathbb{F}_2$, with the non-zero elements represented by $\{ \frac{l}{2}, m, \frac{l}{2}+m \}$. That is,
\[
L_l^* = L_l \sqcup (L_l+m) \sqcup (L_l+\frac{l}{2}) \sqcup (L_l+(\frac{l}{2}+m)) \]
This gives us three lattices
\[
\begin{cases}
M_1 &= L_l \sqcup (L_l+m) = L \\
M_2 &= L_l \sqcup (L_l+\frac{l}{2}) \\
M_3 &= L_l \sqcup (L_l+(\frac{l}{2}+m))
\end{cases}
\]
and all three of them are unimodular because
\[
L_l \subsetneq M_i \subseteq M_i^* \subsetneq L_l^* \]
and $L_l$ is of index $4$ in $L_l^*$.
Now, let’s assume the norm of $l$, that is, $l.l \in 4 \mathbb{Z}$. Then, either the norm of $\frac{l}{2}$ is odd (but then the norm of $\frac{l}{2}+m$ must be even), or the norm of $\frac{l}{2}$ is even, in which case the norm of $\frac{l}{2}+m$ is odd.
That is, either $M_2$ or $M_3$ is an even unimodular lattice, the other one being an odd unimodular lattice.
Let’s take for $l$ and $m$ the vectors $\lambda = \frac{1}{\sqrt{2}} (1,1,\dots,1) \in L – 2L$ and $\mu = \sqrt{2}(1,0,\dots,0) \in L$, then
\[
\lambda.\lambda = \frac{1}{2}\times 24 = 12 \quad \text{and} \quad \mu.\lambda = 1 \]
Because $\frac{\lambda}{2}.\frac{\lambda}{2} = \frac{12}{4}=3$ is odd, we have that
\[
\Lambda = L_{\lambda} \sqcup (L_{\lambda} + (\frac{\lambda}{2} + \mu)) \]
is an even unimodular lattice, which is the Leech lattice, and
\[
\Lambda_{odd} = L_{\lambda} \sqcup (L_{\lambda} + \frac{\lambda}{2}) \]
is an odd unimodular lattice, called the odd Leech lattice.

John Leech (1926-1992) – Photo Credit
Let’s check that these are indeed the Leech lattices, meaning that they do not contain roots (vectors of norm two).
The only roots in $L = (A_1^{24})^+$ are the $48$ roots of $A_1^{24}$ and they are of the form $\pm \sqrt{2} [ 1, 0^{23} ]$, but none of them lies in $L_{\lambda}$ as their inproduct with $\lambda$ is one. So, all non-zero vectors in $L_{\lambda}$ have norm $\geq 4$.
As for the other part of $\Lambda$ and $\Lambda_{odd}$
\[
(L_{\lambda} + \frac{\lambda}{2}) \sqcup (L_{\lambda} + \mu + \frac{\lambda}{2}) = (L_{\lambda} \sqcup (L_{\lambda}+\mu))+\frac{\lambda}{2} = L + \frac{\lambda}{2} \]
From the description of $L=(A_1^{24})^+$ it follows that every coordinate of a vector in $L + \frac{\lambda}{2}$ is of the form
\[
\frac{1}{\sqrt{2}}(v+\frac{1}{2}) \quad \text{or} \quad \frac{1}{\sqrt{2}}(v+\frac{3}{2}) \]
with $v \in 2 \mathbb{Z}$, with the second case instances forming a codeword in $\mathcal{C}_{24}$. In either case, the square of each of the $24$ coordinates is $\geq \frac{1}{8}$, so the norm of such a vector must be $\geq 3$, showing that there are no roots in this region either.
If one takes for $l$ a vector of the form $\frac{1}{\sqrt{2}} v = \frac{1}{\sqrt{2}}[1^a,0^{24-a}]$ where $a=8,12$ or $16$ and $v \in \mathcal{C}_{24}$, takes $m=\mu$ as before, and repeats the construction, one gets the other Niemeier-neighbours of $(A_1^{24})^+$, that is, the lattices $(A_2^{12})^+$, $(A_3^8)^+$ and $(D_4^6)^+$.
For $a=12$ one needs a slightly different argument, see section 0.2 of Richard Borcherds’ Ph.D. thesis.