The Leech lattice neighbour

Here’s the upper part of Kneser‘s neighbourhood graph of the Niemeier lattices:

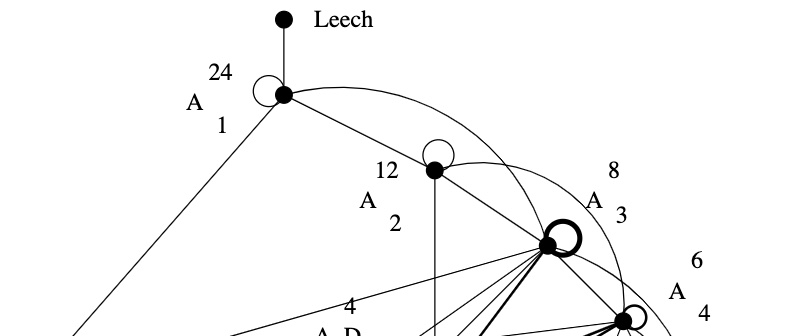
The Leech lattice has a unique neighbour, that is, among the $23$ remaining Niemeier lattices there is a unique one, $(A_1^{24}{)}^{+}$, sharing an index two sub-lattice with the Leech.

How would you try to construct $(A_1^{24}{)}^{+}$, an even unimodular lattice having the same roots as $A_1^{24}$?

The root lattice $A_1$ is $\sqrt{2}\mathbb{Z}$. It has two roots $\pm \sqrt{2}$, determinant $2$, its dual lattice is $A_1^{\ast }=\frac{1}{\sqrt{2}}\mathbb{Z}$ and we have $A_1^{\ast }/A_1\simeq C_2\simeq {\mathbb{F}}_2$.

Thus, $A_1^{24}=\sqrt{2}{\mathbb{Z}}^{\oplus 24}$ has $48$ roots, determinant $2^{24}$, its dual lattice is $(A_1^{24}{)}^{\ast }=\frac{1}{\sqrt{2}}{\mathbb{Z}}^{\oplus 24}$ and the quotient group $(A_1^{24}{)}^{\ast }/A_1^{24}$ is $C_2^{24}$ isomorphic to the additive subgroup of ${\mathbb{F}}_2^{\oplus 24}$.

A larger lattice $A_1^{24}\subseteq L$ of index $k$ gives for the dual lattices an extension $L^{\ast }\subseteq (A_1^{24}{)}^{\ast }$, also of index $k$. If $L$ were unimodular, then the index has to be $2^{12}$ because we have the situation
$$A_1^{24}\subseteq L=L^{\ast }\subseteq (A_1^{24}{)}^{\ast }$$
So, Kneser’s glue vectors form a $12$-dimensional subspace $\mathcal{C}$ in ${\mathbb{F}}_2^{\oplus 24}$, that is,
$$L=\mathcal{C}\underset{{\mathbb{F}}_2}{\times }(A_1^{24}{)}^{\ast }=\{\frac{1}{\sqrt{2}}\overrightarrow{v}|\overrightarrow{v}\in {\mathbb{Z}}^{\oplus 24},v=\overrightarrow{v}mod2\in \mathcal{C}\}$$
Because $L=L^{\ast }$, the linear code $\mathcal{C}$ must be self-dual meaning that $v.w=0$ (in ${\mathbb{F}}_2$) for all $v,w\in \mathcal{C}$. Further, we want that the roots of $A_1^{24}$ and $L$ are the same, so the minimal number of non-zero coordinates in $v\in \mathcal{C}$ must be $8$.

That is, $\mathcal{C}$ must be a self-dual binary code of length $24$ with Hamming distance $8$.

Marcel Golay (1902-1989) – Photo Credit

We now know that there is a unique such code, the (extended) binary Golay code, ${\mathcal{C}}_{24}$, which has

• one vector of weight $0$
• $759$ vectors of weight $8$ (called ‘octads’)
• $2576$ vectors of weight $12$ (called ‘dodecads’)
• $759$ vectors of weight $16$
• one vector of weight $24$

The $759$ octads form a Steiner system $S(5,8,24)$ (that is, for any $5$-subset $S$ of the $24$-coordinates there is a unique octad having its non-zero coordinates containing $S$).

Witt constructed a Steiner system $S(5,8,24)$ in his 1938 paper “Die $5$-fach transitiven Gruppen von Mathieu”, so it is not unthinkable that he checked the subspace of ${\mathbb{F}}_2^{\oplus 24}$ spanned by his $759$ octads to be $12$-dimensional and self-dual, thereby constructing the Niemeier-lattice $(A_1^{24}{)}^{+}$ on that sunday in 1940.

John Conway classified all nine self-dual codes of length $24$ in which the weight
of every codeword is a multiple of $4$. Each one of these codes $\mathcal{C}$ gives a Niemeier lattice $\mathcal{C}\underset{{\mathbb{F}}_2}{\times }(A_1^{24}{)}^{\ast }$, all but one of them having more roots than $A_1^{24}$.

Vera Pless and Neil Sloan classified all $26$ binary self-dual codes of length $24$.