Skip to content →

Category: number theory

the Riemann hypothesis and Psi

Published July 14, 2019 by lieven

Last time we revisited Robin’s theorem saying that 5040 being the largest counterexample to the bound
\[
\frac{\sigma(n)}{n~log(log(n))} < e^{\gamma} = 1.78107... \] is equivalent to the Riemann hypothesis.

There’s an industry of similar results using other arithmetic functions. Today, we’ll focus on Dedekind’s Psi function
\[
\Psi(n) = n \prod_{p | n}(1 + \frac{1}{p}) \]
where $p$ runs over the prime divisors of $n$. It is series A001615 in the online encyclopedia of integer sequences and it starts off with

1, 3, 4, 6, 6, 12, 8, 12, 12, 18, 12, 24, 14, 24, 24, 24, 18, 36, 20, 36, 32, 36, 24, 48, 30, 42, 36, 48, 30, 72, 32, 48, 48, 54, 48, …

and here’s a plot of its first 1000 values



To understand this behaviour it is best to focus on the ‘slopes’ $\frac{\Psi(n)}{n}=\prod_{p|n}(1+\frac{1}{p})$.

So, the red dots of minimal ‘slope’ $\approx 1$ correspond to the prime numbers, and the ‘outliers’ have a maximal number of distinct small prime divisors. Look at $210 = 2 \times 3 \times 5 \times 7$ and its multiples $420,630$ and $840$ in the picture.

For this reason the primorial numbers, which are the products of the fist $k$ prime numbers, play a special role. This is series A002110 starting off with

1, 2, 6, 30, 210, 2310, 30030, 510510, 9699690, 223092870,…

In Patrick Solé and Michel Planat Extreme values of the Dedekind $\Psi$ function, it is shown that the primorials play a similar role for Dedekind’s Psi as the superabundant numbers play for the sum-of-divisors function $\sigma(n)$.

That is, if $N_k$ is the $k$-th primorial, then for all $n < N_k$ we have that the 'slope' at $n$ is strictly below that of $N_k$ \[ \frac{\Psi(n)}{n} < \frac{\Psi(N_k)}{N_k} \] which follows immediately from the fact that any $n < N_k$ can have at most $k-1$ distinct prime factors and $p \mapsto 1 + \frac{1}{p}$ is a strictly decreasing function.

Another easy, but nice, observation is that for all $n$ we have the inequalities
\[
n^2 > \phi(n) \times \psi(n) > \frac{n^2}{\zeta(2)} \]
where $\phi(n)$ is Euler’s totient function
\[
\phi(n) = n \prod_{p | n}(1 – \frac{1}{p}) \]
This follows as once from the definitions of $\phi(n)$ and $\Psi(n)$
\[
\phi(n) \times \Psi(n) = n^2 \prod_{p|n}(1 – \frac{1}{p^2}) < n^2 \prod_{p~\text{prime}} (1 - \frac{1}{p^2}) = \frac{n^2}{\zeta(2)} \] But now it starts getting interesting.

In the proof of his theorem, Guy Robin used a result of his Ph.D. advisor Jean-Louis Nicolas



known as Nicolas’ criterion for the Riemann hypothesis: RH is true if and only if for all $k$ we have the inequality for the $k$-th primorial number $N_k$
\[
\frac{N_k}{\phi(N_k)~log(log(N_k))} > e^{\gamma} \]
From the above lower bound on $\phi(n) \times \Psi(n)$ we have for $n=N_k$ that
\[
\frac{\Psi(N_k)}{N_k} > \frac{N_k}{\phi(N_k) \zeta(2)} \]
and combining this with Nicolas’ criterion we get
\[
\frac{\Psi(N_k)}{N_k~log(log(N_k))} > \frac{N_k}{\phi(N_k)~log(log(N_k)) \zeta(2)} > \frac{e^{\gamma}}{\zeta(2)} \approx 1.08… \]
In fact, Patrick Solé and Michel Planat prove in their paper Extreme values of the Dedekind $\Psi$ function that RH is equivalent to the lower bound
\[
\frac{\Psi(N_k)}{N_k~log(log(N_k))} > \frac{e^{\gamma}}{\zeta(2)} \]
holding for all $k \geq 3$.

Dedekind’s Psi function pops up in lots of interesting mathematics.

In the theory of modular forms, Dedekind himself used it to describe the index of the congruence subgroup $\Gamma_0(n)$ in the full modular group $\Gamma$.

In other words, it gives us the number of tiles needed in the Dedekind tessellation to describe the fundamental domain of the action of $\Gamma_0(n)$ on the upper half-plane by Moebius transformations.

When $n=6$ we have $\Psi(6)=12$ and we can view its fundamental domain via these Sage commands:


G=Gamma0(6)
FareySymbol(G).fundamental_domain()

giving us the 24 back or white tiles (note that these tiles are each fundamental domains of the extended modular group, so we have twice as many of them as for subgroups of the modular group)



But, there are plenty of other, seemingly unrelated, topics where $\Psi(n)$ appears. To name just a few:

  • The number of points on the projective line $\mathbb{P}^1(\mathbb{Z}/n\mathbb{Z})$.
  • The number of lattices at hyperdistance $n$ in Conway’s big picture.
  • The number of admissible maximal commuting sets of operators in the Pauli group for the $n$ qudit.

and there are explicit natural one-to-one correspondences between all these manifestations of $\Psi(n)$, tbc.

Comments closed

the Riemann hypothesis and 5040

Published July 7, 2019 by lieven

Yesterday, there was an interesting post by John Baez at the n-category cafe: The Riemann Hypothesis Says 5040 is the Last.

The 5040 in the title refers to the largest known counterexample to a bound for the sum-of-divisors function
\[
\sigma(n) = \sum_{d | n} d = n \sum_{d | n} \frac{1}{d} \]

In 1983, the french mathematician Guy Robin proved that the Riemann hypothesis is equivalent to
\[
\frac{\sigma(n)}{n~log(log(n))} < e^{\gamma} = 1.78107... \] when $n > 5040$.

The other known counterexamples to this bound are the numbers 3,4,5,6,8,9,10,12,16,18,20,24,30,36,48,60,72,84,120,180,240,360,720,840,2520.




In Baez’ post there is a nice graph of this function made by Nicolas Tessore, with 5040 indicated with a grey line towards the right and the other counterexamples jumping over the bound 1.78107…



Robin’s theorem has a remarkable history, starting in 1915 with good old Ramanujan writing a part of this thesis on “highly composite numbers” (numbers divisible by high powers of primes).

His PhD. adviser Hardy liked his result but called them “in the backwaters of mathematics” and most of it was not published at the time of Ramanujan’s degree ceremony in 1916, due to paper shortage in WW1.



When Ramanujan’s paper “Highly Composite Numbers” was first published in 1988 in ‘The lost notebook and other unpublished papers’ it became clear that Ramanujan had already part of Robin’s theorem.

Ramanujan states that if the Riemann hypothesis is true, then for $n_0$ large enough we must have for all $n > n_0$ that
\[
\frac{\sigma(n)}{n~log(log(n))} < e^{\gamma} = 1.78107... \] When Jean-Louis Nicolas, Robin's PhD. adviser, read Ramanujan's lost notes he noticed that there was a sign error in Ramanujan's formula which prevented him from seeing Robin's theorem.

Nicolas: “Soon after discovering the hidden part, I read it and saw the difference between Ramanujan’s result and Robin’s one. Of course, I would have bet that the error was in Robin’s paper, but after recalculating it several times and asking Robin to check, it turned out that there was an error of sign in what Ramanujan had written.”

If you are interested in the full story, read the paper by Jean-Louis Nicolas and Jonathan Sondow: Ramanujan, Robin, Highly Composite Numbers, and the Riemann Hypothesis.

What’s the latest on Robin’s inequality? An arXiv-search for Robin’s inequality shows a flurry of activity.

For starters, it has been verified for all numbers smaller that $10^{10^{13}}$…

It has been verified, unconditionally, for certain classes of numbers:

  • all odd integers $> 9$
  • all numbers not divisible by a 25-th power of a prime

Rings a bell? Here’s another hint:

According to Xiaolong Wu in A better method than t-free for Robin’s hypothesis one can replace the condition of ‘not divisible by an N-th power of a prime’ by ‘not divisible by an N-th power of 2’.

Further, he claims to have an (as yet unpublished) argument that Robin’s inequality holds for all numbers not divisible by $2^{42}$.

So, where should we look for counterexamples to the Riemann hypothesis?

What about the orders of huge simple groups?

The order of the Monster group is too small to be a counterexample (yet, it is divisible by $2^{46}$). 2 Comments

G+ recovery 5 : #IUTeich (3)

Published February 5, 2019 by lieven

The final part, starting with a reaction of Mochizuki himself on my previous IUTeich-posts.

July 7th, 2013

Mochizuki update

While i’ve been away from G+, someone emailed Mochizuki my last post on the problem i have with Frobenioids1. He was kind enough to forward  me M’s reply:

“There is absolutely nothing difficult or subtle going on here (e.g., by comparison to the portion of the theory cited in the discussion preceding the statement of this “problem”!).  The nontrivial result is the fact that the degree is rational, i.e., the initial portion of [FrdI], Theorem 6.4, (iii), which is a consequence of a highly nontrivial result in transcendence theory due to Lang (i.e., [FrdI], Lemma 6.5, (ii)).  Once one knows this rationality, the conclusion that distinct prime numbers are not confused with one another is a formal consequence (i.e., no complicated subtle arguments!) of the fact that the ratio of the natural logarithm of any two distinct prime numbers is never rational.
Sincerely, Shinichi Mochizuki”

Being back, i’ll give it another go.

Having read the shared article below (2/5/2019 ‘the paradox of the proof’), it’s comforting to know that other people, including  +Aise Johan de Jong and +Cathy O’Neil, are also frustrated by M’s opaque latest writings.

July 11th, 2013

Mochizuki’s Frobenioid reconstruction: the final bit

In “The geometry of Frobenioids 1” Mochizuki ‘dismantles’ arithmetic schemes and replaces them by huge categories called Frobenioids. Clearly, one then wants to reconstruct the schemes from these categories and we almost understood how he manages to to this, modulo the ‘problem’ that there might be auto-equivalences of $Frob(\mathbb{Z})$, the Frobenioid corresponding to $\mathbf{Spec}(\mathbb{Z})$ i.e.the collection of all prime numbers, reshuffling distinct prime numbers.

In previous posts i’ve simplified things a lot, leaving out the ‘Arakelov’ information contained in the infinite primes, and feared that this lost info might be crucial to understand the final bit. Mochizuki’s email also points in that direction.

Here’s what i hope to have learned this week:

the full Frobenioid $Frob(\mathbb{Z})$

objects of $Frob(\mathbb{Z})$ consist of pairs $(q,r)$ where $q$ is a strictly positive rational number and $r$ is a real number.

morphisms are of the form $f=(n,a,(z,s)) : (q,r) \rightarrow (q’,r’)$ (where $n$ and $z$ are strictly positive integers, $a$ a strictly positive rational number and $s$ a positive real number) subject to the relations that

\[
q^n.z = q’.a  \quad \text{and} \quad n.r+s = r’+log(a) \]

$n$ is called the Frobenious degree of $f$ and $(z,s)$ the divisor of $f$.

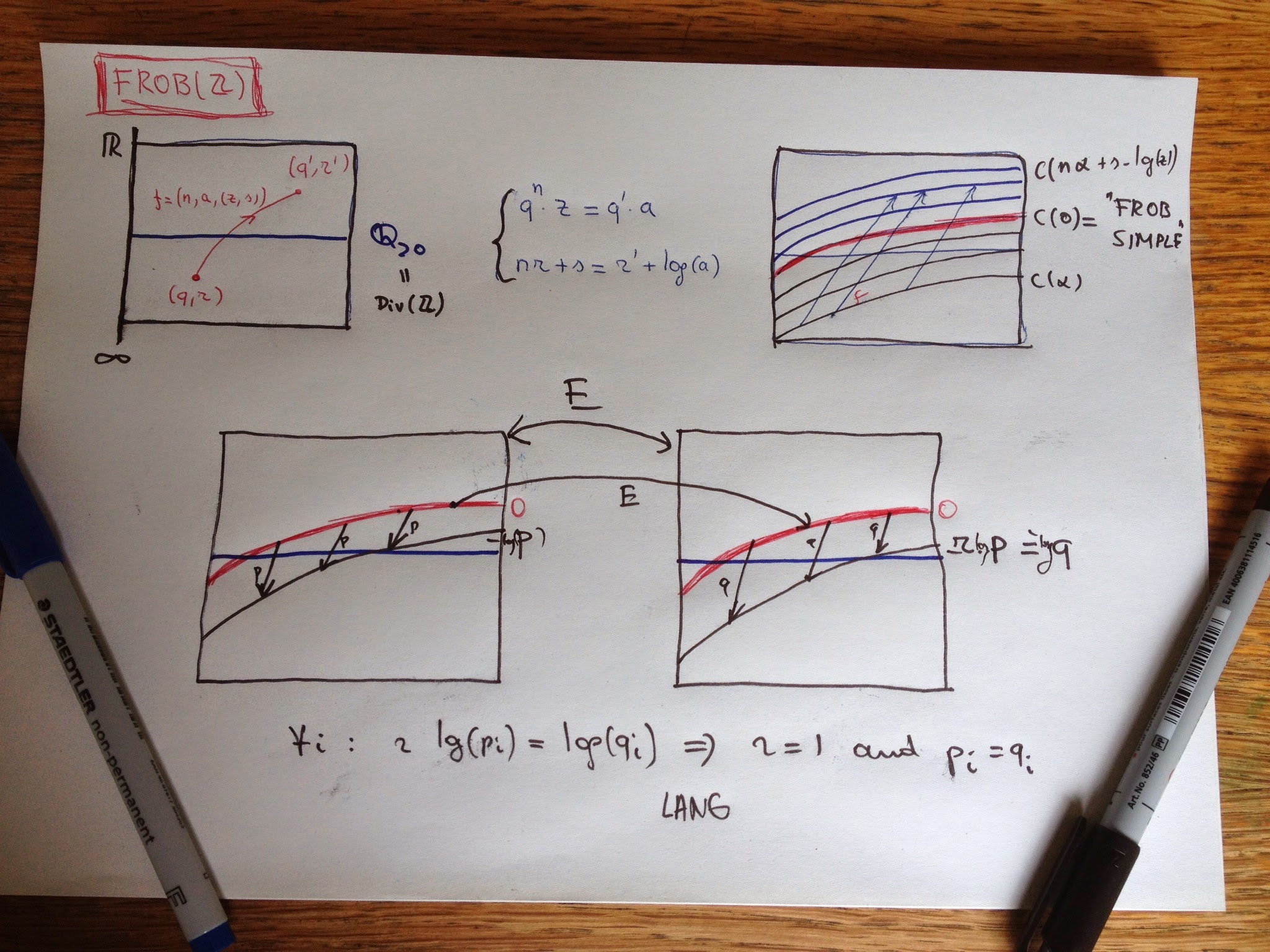
All this may look horribly complicated until you realise that the isomorphism classes in $Frob(\mathbb{Z})$ are exactly the ‘curves’ $C(\alpha)$ consisting of all pairs $(q,r)$ such that $r-log(q)=\alpha$, and that morphisms with the same parameters as $f$ send points in $C(\alpha)$ to points in $C(\beta)$ where

\[
\beta = n.\alpha + s – log(a) \]

So, the isomorphism classes can be identified with the real numbers $\mathbb{R}$ and special linear morphisms of type $(1,a,(1,s))$ and their compositions are compatible with the order-structure and addition on $\mathbb{R}$.

Crucial is Mochizuki’s observation that $C(0)$ are precisely the ‘Frobenious-trivial’ objects in $Frob(\mathbb{Z})$ (i’ll spare you the details but it is a property on having sufficiently many nice endomorphisms).

Now, consider an auto-equivalence $E$ of $Frob(\mathbb{Z})$. It will induce a map between the isoclasses $E : \mathbb{R} \rightarrow \mathbb{R}$ which is additive and as Frob-trivs are mapped under $E$ to Frob-trivs this will map $0$ to $0$, so $E$ will be an additive group-endomorphism on $\mathbb{R}$ hence of the form $x \rightarrow r.x$ for some fixed real number $r$, and we want to show that $r=1$.

Linear irreducible morphisms are of type $(1,a,(p,0))$ where $p$ is a prime number and they map $C(\alpha)$ to $C(\alpha-log(p))$. As irreducibles are preserved under equivalence this means that for each prime $p$ there must exist a prime $q$ such that $r log(p) = log(q)$.

Now if $r$ is an irrational number, there must be at least three triples $(p_1,q_1),(p_2,q_2)$ and $(p_3,q_3)$ satisfying $r log(p_i) = log(q_i)$ but this contradicts a fairly hard result, due to Lang, that for 6 distinct primes l_1,…,l_6 there do not exist positive rational numbers $a,b$ such that

\[
log(l_1)/log(l_2) = a log(l_3)/log(l_4) = b log(l_5)/log(l_6) \]

So, $r$ must be rational and of the form $n/m$, but then $r=1$ (if not the correspondence $r.log(p) = log(q)$ gives $p^n=q^m$ contradicting unique factorisation). This then shows that under the auto-equivalence each prime $p$ (corresponding to a linear irreducible map) is send to itself.

This was the remaining bit left to show that the Frobenioid corresponding to any Galois extension of the rationals contains enough information to reconstruct from it the schemes of all rings of integers in intermediate fields.

August 15th, 2013

Szpiro’s Marabout-Flash on number theory

For travellers into Mochizuki-territory the indispensable rough guide is Lucien Szpiro’s ‘Marabout-Flash de théorie des nombres algébriques’, aka section I.1.3 in  ‘Séminaire sur les pinceaux arithmétiques: la conjecture de Mordell’.

Marabout Flash was a Franco-Belge series of do-it-yourself booklets, quite popular in the 60ties and 70ties, on almost every aspect of everyday’s life.

In just a couple of pages Szpiro describes how one can extend the structure sheaf of a fractional ideal of a ring of integers to a ‘metrized’ (or Arakelov) line-bundle on the completed prime spectrum (including the infinite places). These bundles then satisfy properties similar to those of line-bundles on smooth projective curves, including a version of the Riemann-Roch theorem and a criterium to have non-zero global sections.

These (fairly simple) results then quickly lead to proofs of the first major results in number theory such as the Hermite-Minkowski theorem and Dirichlet’s unit theorem.

December 29th, 2014

Mochizuki in denial

From M’s 2014 IUTeich-Progress-Report (17 pages, the 2013-edition was only 7 pages long):

“Activities surrounding IUTeich appears to be in a stage of transition from a focus on verification to a focus on dissemination.”

If only…

He further lists hypotheses as to why nobody (apart from his 3 disciples Yamashita,Saidi and Hoshi) makes a serious effort to “study the theory carefully and systematically from the beginning”:

1. it is too long (1500-2500 pages)
2. there’s lack of textbooks on anabelian geometry
3. we are obsessed with the Langlands program
4. there’s little room for generalisations
5. it may not be directly useful for our own research

But then, why should anyone make such an effort, as:

“With the exception of the handful of researchers already involved in the verification activities concerning IUTeich, every researcher in arithmetic geometry throughout the world is a complete novice with respect to the mathematics surrounding IUTeich, and hence, in particular, is simply not qualified to issue a definite judgment concerning the validity of IUTeich on the basis of a ‘deep understanding’ arising from his/her previous research achievements.”

No Mochizuki, the next phase will not be dissemination, it will be denial.

Other remarkable sentences are:

“IUTeich is ‘the correct theory’ in the sense that it leads one to doubt the existence of any sort of ‘alternative proof’, i.e. via essentially different techniques, of the ABC Conjecture.”

and:

“the status of IUTeich in the field of arithmetic geometry constitutes a sort of faithful miniature model of the status of pure mathematics in human society.”

Already looking forward to the 2015 ‘progress’ report…

October 8th, 2015

Proud to be working at a well-known university

First time I’m mentioned in “Nature”, they issue this correction:

Corrected: An earlier version of this story incorrectly located the University of Antwerp in the Netherlands. It is in Belgium. The text has been updated.

Not particularly proud of the quote they took from my blog though:

“Is it just me, or is Mochizuki really sticking up his middle finger to the mathematical community”.

December 17th, 2017

We’re heading for a bad ending

Yesterday, my feeds became congested by (Japanese) news saying that Mochizuki’s (claimed) proof of the abc-conjecture had been vetted and considered fit to be published in a respectable journal.

Today, long term supporters of M’s case began their Echternachian-retreat after finding out that Mochizuki himself is the editor in charge of that respectable journal.

Attached is Ed Frenkel’s retraction of his previous tweet. Also, Taylor Dupuy deemed the latest action a bridge too far, see here.

Peter Woit did a great job in his recent post
pinpointing a critical argument in the 500-page long papers having as its “proof” that it followed trivially from the definitions…

I’d expect any board of editors to resign in such a case.
I fear this can only end badly.

One Comment