The Dedekind tessellation

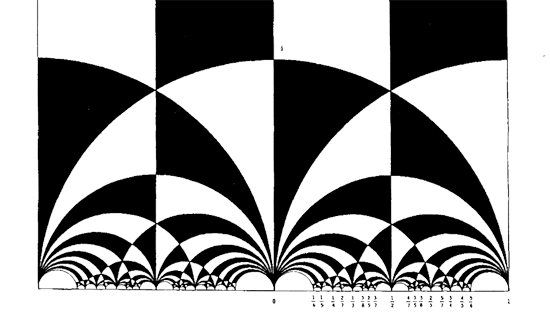
In 1877, Richard Dedekind discovered one of the most famous pictures in mathematics : the black&white tessellation of the upper half-plane in hyperbolic triangles. Recall that the group $S{L}_2(\mathbb{Z})$ of all invertible 2×2 integer matrices with determinant $1$ acts on the upper halfplane via

$\left[\begin{array}{cc}a& b\\ c& d\end{array}\right].z=\frac{az+b}{cz+d}$

and as minus the identity matrix acts trivially, it is really an action of the modular group $\mathrm{\Gamma }=PS{L}_2(\mathbb{Z})$. Any black or white triangle in the Dedekind-tessellation is a fundamental domain for the action of the extended modular group ${\mathrm{\Gamma }}^{\ast }$, generated by $\mathrm{\Gamma }$ and the morphism $z\mapsto –\bar{z}$. . Dedekind showed that the union of any back and white region is a fundamental domain for the action of the modular group. For example, the ‘usual’ fundamental domain is the union of the top middle black and white regions in Dedekinds picture. Having this tessellation before you is essential if you have to wade through the heavy notation of the important paper by Ravi Kulkarni “An arithmetic-geometric method in the study of the subgroups of the modular group”, which is what we aim to do now. Applications will be given in future posts in this series.

At some points (such as $i$) two black and two white regions are coming together, we call such points even vertices and they form the ${\mathrm{\Gamma }}^{\ast }$-orbit of $i$.
At other points (such as $\rho =e^{\frac{\pi i}{3}}$) three black and white regions are meeting and we call such points odd vertices (they form the ${\mathrm{\Gamma }}^{\ast }$-orbit of $\rho$). The ${\mathrm{\Gamma }}^{\ast }$-orbit of $\mathrm{\infty }$ consists of the rational numbers and they are called the cusps.

Now, for the edges. There are three types of edges : even edges connecting a cusp and an even vertex (they form the ${\mathrm{\Gamma }}^{\ast }$-orbit of the line $(\mathrm{\infty },i)$), odd edges connecting a cusp to an odd vertex (the translates of $(\mathrm{\infty },\rho )$) and finally f-edges (f for finite) connecting an odd and even vertex (the ${\mathrm{\Gamma }}^{\ast }$-orbit of the arc $(\rho ,i)$).

The geodesics (the semi-circles and the vertical lines) are made of edges and they come in two types : even lines are complete geodesics which are unions of two even edges (such as the semi-circle $(0,1)$) and odd lines (such as the semi-circle $(-1,1)$) are complete geodesics which are unions of two f-edges and two odd edges. Remark that the vertical lines are even if they pass through an integer and odd when they go through a half-integer. The modular group $\mathrm{\Gamma }$ acts transitively on the even (resp. odd) lines.

If we write rational numbers in reduced form $\frac{a}{b}$ (and if we agree to write integers as $\frac{n}{1}$ and $\mathrm{\infty }=\frac{1}{0}$) then, if a geodesic has endpoints $\frac{a}{b}$ and $\frac{c}{d}$ it is an even line iff $|ad-bc|=1$ and an odd line iff $|ad-bc|=2$.

This notation was set up to define the notion of a special polygon which is a connected polygonal region $P$ in the upper-halfplane such that its boundary $\partial P$ consists entirely of even and odd edges (so no f-edges) together with a side-pairing satisfying the following requirements

1. Even edges in $\partial P$ come in pairs and each such pair forms an even line.
2. Odd edges in $\partial P$ come in pairs and each pair meets at an odd vertex where they make an internal angle of $\frac{2\pi }{3}$.
3. Any odd edge e is side-paired to a different odd edge f which makes on internal angle $\frac{2\pi }{3}$ with e.
4. If e and f are even edges in $\partial P$ forming an even line, then either e is side-paired to f or else e,f form a free side and is side-paired to a different such free side.
5. $0,\mathrm{\infty }$ are among the vertices of $P$.

The sides of P are : the odd edges on the boundary, the free sides and the even edges on non-free sides. The vertices of P are the intersections of adjacent sides.

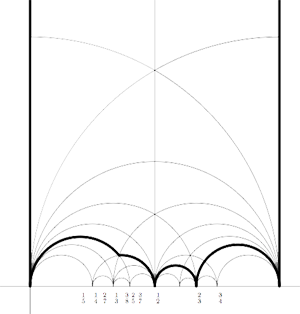For example, the region inside the thick edges is a special polygon. Its boundary consists of 8 even edges (two on the 4 complete geodesics : the vertical lines at 0 and 1 and the semi-circles $(\frac{1}{2},\frac{2}{3})$ and $(\frac{2}{3},1)$) and 2 odd edges the arc-fragments in the lower left corner, the leftmost being part of the semi-circle $(0,\frac{1}{3})$, the other part of the semi-circle $(\frac{1}{4},\frac{1}{2})$.

We have several option for the side-pairing, the only forded pairing being the two odd edges which have to be paired. For the even edges we can either consider 0,2 or 4 of the geodesics as free sides and pair these, or we can have 0,2 or 4 non-free sides and then we have to pair up the two even edges making such a non-free side.

The number of sides of the special polygon depends on the number of free sides chosen. For 0 free sides, there are 10 sides and vertices. For 2 free sides, there are 8 sides and vertices and for 4 free sides we have 6 sides and vertices.

Special polygons are a combinatorial gadget to describe the subgroups of finite index in the modular group $PS{L}_2(\mathbb{Z})$. Later, we will connect this notion to _quilts_ which are special ‘dessins d’enfants’ and to generalized _Farey sequences_. This will then allow us to find explicit generators of the subgroups.

Some technical issues : if some of the latex-pictures don’t show up nicely it often helps to resize the browser-window and resize it back. The drawing of the special polygon was made using the LaTeX-package MFPIC which is an easy to use interface to MetaPost.

Reference

Ravi S. Kulkarni “An arithmetic-geometric method in the study of the subgroups of the modular group” Amer. J. Math. 113 (1991) 1053-1133