The usual argument to show that the group of all orientation-preserving symmetries of the Klein quartic is the simple group $L_2(7)$ of order $168$ goes like this:
There are two families of $7$ truncated cubes on the Klein quartic. The triangles of one of the seven truncated cubes in the first family have as center the dots, all having the same colour. The triangles of one of the truncated cubes in the second family correspond to the squares all having the same colour.
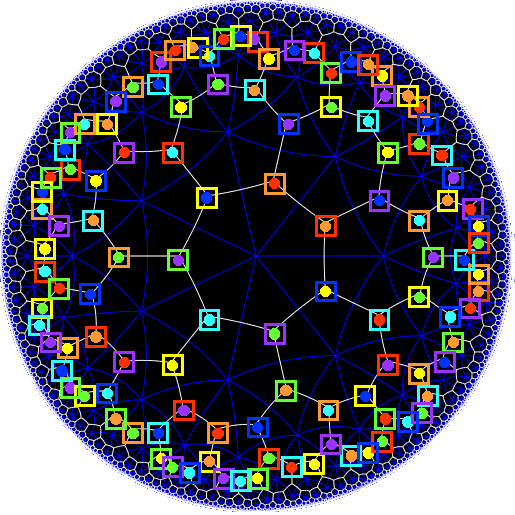
If you compare the two colour schemes, you’ll see that every truncated cube in the first family is disjoint from precisely $3$ truncated cubes in the second family.
That is, we can identify the truncated cubes of the first family with the points in the Fano plane $\mathbb{P}^2(\mathbb{F}_2)$, and those of the second family with the lines in that plane.
The Klein quartic consists of $24$ regular heptagons, so its rotation symmetry group consists of $24 \times 7 = 168$ rotations,each preserving the two families of truncated cubes. This is exactly the same number as there are isomorphisms of the Fano plane, $PGL_3(\mathbb{F}_2) = L_2(7)$. Done!
For more details, check John Baez’ excellent page on the Klein quartic, or the Buckyball curve post.
Here’s another ‘look-and-see’ proof, starting from Klein’s own description of his quartic.
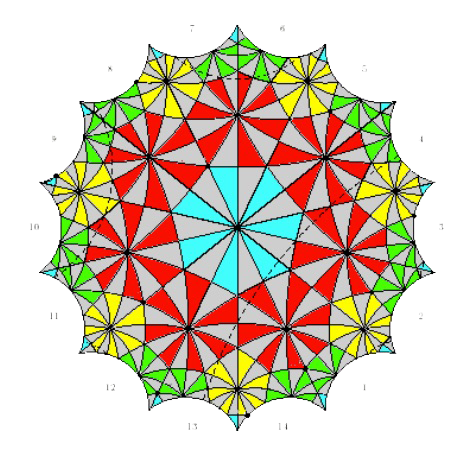
Look at the rotation $g$, counter-clockwise with angle $2\pi / 7$ fixing the center of the central blue heptagon, and a similar rotation $h$ fixing the center of one of the neighbouring red heptagons.
The two vertices of the edge shared by the blue and red heptagon are fixed by $g.h$ and $h.g$, respectively, so these rotations must have order three (there are $3$ heptagons meeting in the vertex).
That is, the rotation symmetry group $G$ of the Klein quartic has order $168$, and contains two elements $g$ and $h$ of order $7$, such that the subgroup generated by them contains elements of order $3$.
This is enough to prove that the $G$ must be simple and therefore isomorphic to $L_2(7)$!
The following elegant proof is often attributed to Igor Dolgachev.
If $G$ isn’t simple there is a maximal normal subgroup $N$ with $G/N$ simple .
The only non-cyclic simple group having less elements that $168$ is $A_5$ but this cannot be $G/N$ as $60$ does not divide $168$.
So, $G/N$ must be cyclic of order $2,3$ or $7$ (the only prime divisors of $168=2^3.3.7$).
Order $2$ is not possible as any group $N$ of order $84=2^2.3.7$ can just have one Sylow $7$-subgroup. Remember that the number of $7$-Sylows of $N$ must divide $2^2.3=12$ and must be equal to $1$ modulo $7$. And $G$ (and therefore $N$) has at least two different cyclic subgroups of order $7$.
Order $3$ is impossible as this would imply that the normal subgroup $N$ of order $2^3.7=56$ must contain all $7$-Sylows of $G$, and thus also an element of order $3$. But, $3$ does not divide $56$.
Order $7$ is a bit more difficult to exclude. This would mean that there is a normal subgroup $N$ of order $2^3.3=24$.
$N$ (being normal) must contain all Sylow $2$-subgroups of $G$ of which there are either $1$ or $3$ (the order of $N$ is $2^3.3=24$).
If there is just one $S$ it should be a normal subgroup with $G/S$ (of order $21$) having a (normal) unique Sylow $7$-subgroup, but then $G$ would have a normal subgroup of index $3$, which we have excluded.
The three $2$-Sylows are conjugated and so the conjugation morphism
\[
G \rightarrow S_3 \]
is non-trivial and must have image strictly larger than $C_3$ (otherwise, $G$ would have a normal subgroup of index $3$), so must be surjective.
But, $S_3$ has a normal subgroup of index $2$ and pulling this back, $G$ must also have a normal subgroup of index two, which we have excluded. Done!
Comments closed

