the moonshine picture – at last

The monstrous moonshine picture is the subgraph of Conway’s big picture consisting of all lattices needed to describe the 171 moonshine groups.

It consists of:

– exactly 218 vertices (that is, lattices), out of which

– 97 are number-lattices (that is of the form $M$ with $M$ a positive integer), and

– 121 are proper number-like lattices (that is of the form $M\frac{g}{h}$ with $M$ a positive integer, $h$ a divisor of $24$ and $1\le g\le h$ with $(g,h)=1$).

The $97$ number lattices are closed under taking divisors, and the corresponding Hasse diagram has the following shape

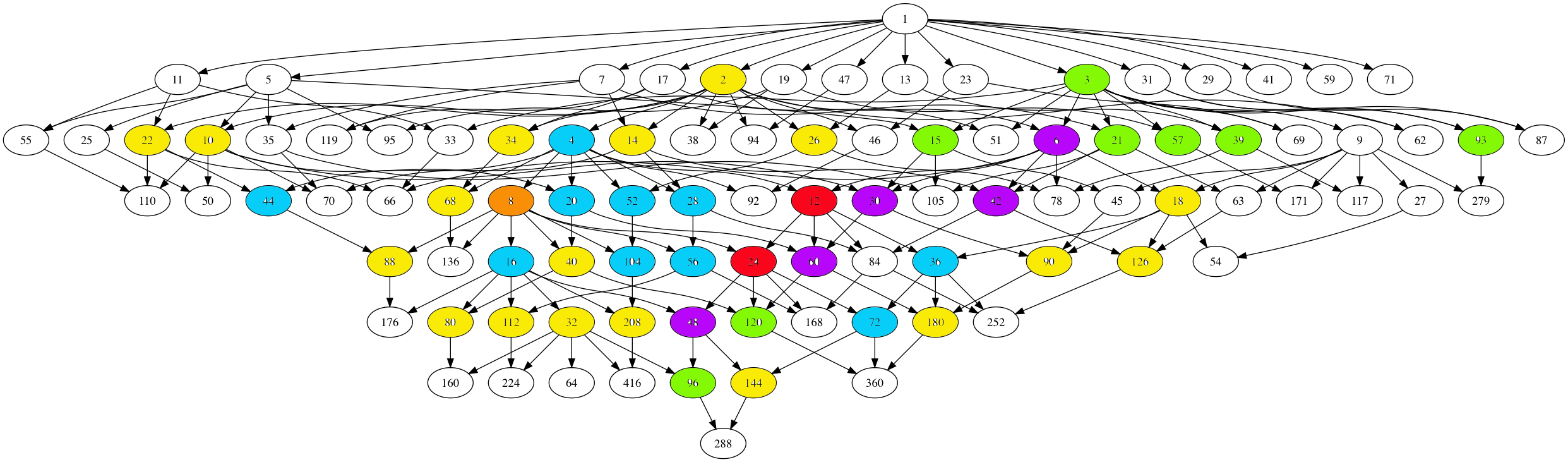
Here, number-lattices have the same colour if they have the same local structure in the moonshine picture (that is, have a similar neighbourhood of proper number-like lattices).

There are 7 different types of local behaviour:

The white numbered lattices have no proper number-like neighbours in the picture.

The yellow number lattices (2,10,14,18,22,26,32,34,40,68,80,88,90,112,126,144,180,208 = 2M) have local structure

which involves all $2$-nd (square) roots of unity centered at the lattice.

The green number lattices (3,15,21,39,57,93,96,120 = 3M) have local structure

which involve all $3$-rd roots of unity centered at the lattice.

The blue number lattices (4,16,20,28,36,44,52,56,72,104 = 4M) have as local structure

and involve the $2$-nd and $4$-th root of unity centered at the lattice.

The purple number lattices (6,30,42,48,60 = 6M) have local structure

and involve all $2$-nd, $3$-rd and $6$-th roots of unity centered at the lattice.

The unique brown number lattice 8 has local structure

which involves all $2$-nd, $4$-th and $8$-th roots of unity centered at $8$.

Finally, the local structure for the central red lattices $12,24=12M$ is

It involves all $2$-nd, $3$-rd, $4$-th, $6$-th and $12$-th roots of unity with center $12M$.

No doubt this will be relevant in connecting moonshine with non-commutative geometry and issues of replicability as in Plazas’ paper Noncommutative Geometry of Groups like ${\mathrm{\Gamma }}_0(N)$.

Another of my pet follow-up projects is to determine whether or not the monster group $\mathbb{M}$ dictates the shape of the moonshine picture.

That is, can one recover the 97 number lattices and their partition in 7 families starting from the set of element orders of $\mathbb{M}$, applying some set of simple rules?

One of these rules will follow from the two equivalent notations for lattices, and the two different sets of roots of unities centered at a given lattice. This will imply that if a number lattice belongs to a given family, certain divisors and multiples of it must belong to related families.

If this works out, it may be a first step towards a possibly new understanding of moonshine.