Last time we have that that one can represent (the conjugacy class of) a finite index subgroup of the modular group $\Gamma = PSL_2(\mathbb{Z}) $ by a Farey symbol or by a dessin or by its fundamental domain. Today we will associate a quiver to it.
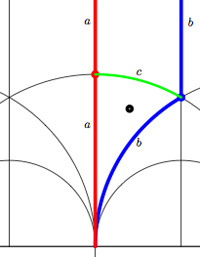For example, the modular group itself is represented by the Farey symbol
[tex]\xymatrix{\infty \ar@{-}[r]_{\circ} & 0 \ar@{-}[r]_{\bullet} & \infty}[/tex] or by its dessin (the green circle-edge) or by its fundamental domain which is the region of the upper halfplane bounded by the red and blue vertical boundaries. Both the red and blue boundary consist of TWO edges which are identified with each other and are therefore called a and b. These edges carry a natural orientation given by circling counter-clockwise along the boundary of the marked triangle (or clockwise along the boundary of the upper unmarked triangle having $\infty $ as its third vertex). That is the edge a is oriented from $i $ to $0 $ (or from $i $ to $\infty $) and the edge b is oriented from $0 $ to $\rho $ (or from $\infty $ to $\rho $) and the green edge c (which is an inner edge so carries no identifications) from $\rho $ to $i $. That is, the fundamental region consists of two triangles, glued together along their boundary which is the oriented cycle $\vec{abc} $ consistent with the fact that the compactification of $\mathcal{H}/\Gamma $ is the 2-sphere $S^2 = \mathbb{P}^1_{\mathbb{C}} $. Under this identification the triangle-boundary abc can be seen to circle the equator whereas the top triangle gives the upper half sphere and the lower triangle the lower half sphere. Emphasizing the orientation we can depict the triangle-boundary as the quiver
[tex]\xymatrix{i \ar[rd]_a & & \rho \ar[ll]_c \\ & 0 \ar[ru]_b}[/tex]
embedded in the 2-sphere. Note that quiver is just a fancy name for an oriented graph…
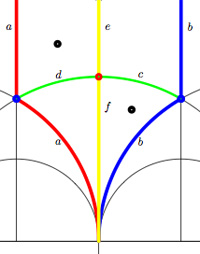Okay, let’s look at the next case, that of the unique index 2 subgroup $\Gamma_2 $ represented by the Farey symbol [tex]\xymatrix{\infty \ar@{-}[r]_{\bullet} & 0 \ar@{-}[r]_{\bullet} & \infty}[/tex] or the dessin (the two green edges) or by its fundamental domain consisting of the 4 triangles where again the left and right vertical boundaries are to be identified in parts.
That is we have 6 edges on the 2-sphere $\mathcal{H}/\Gamma_2 = S^2 $ all of them oriented by the above rule. So, for example the lower-right triangle is oriented as $\vec{cfb} $. To see how this oriented graph (the quiver) is embedded in $S^2 $ view the big lower region (cdab) as the under hemisphere and the big upper region (abcd) as the upper hemisphere. So, the two green edges together with a and b are the equator and the remaining two yellow edges form the two parts of a bigcircle connecting the north and south pole. That is, the graph are the cut-lines if we cut the sphere in 4 equal parts. The corresponding quiver-picture is
[tex]\xymatrix{& i \ar@/^/[dd]^f \ar@/_/[dd]_e & \\
\rho^2 \ar[ru]^d & & \rho \ar[lu]_c \\
& 0 \ar[lu]^a \ar[ru]_b &}[/tex]
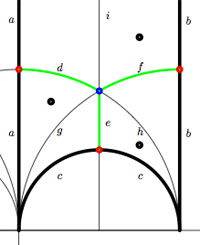As a mental check, verify that the index 3 subgroup determined by the Farey symbol [tex]\xymatrix{\infty \ar@{-}[r]_{\circ} & 0 \ar@{-}[r]_{\circ} & 1 \ar@{-}[r]_{\circ} & \infty}[/tex] , whose fundamental domain with identifications is given on the left, has as its associated quiver picture
[tex]\xymatrix{& & \rho \ar[lld]_d \ar[ld]^f \ar[rd]^e & \\
i \ar[rrd]_a & i+1 \ar[rd]^b & & \omega \ar[ld]^c \\
& & 0 \ar[uu]^h \ar@/^/[uu]^g \ar@/_/[uu]_i &}[/tex]
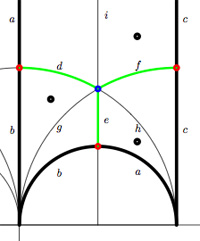whereas the index 3 subgroup determined by the Farey symbol [tex]\xymatrix{\infty \ar@{-}[r]_{1} & 0 \ar@{-}[r]_{1} & 1 \ar@{-}[r]_{\circ} & \infty}[/tex], whose fundamental domain with identifications is depicted on the right, has as its associated quiver
[tex]\xymatrix{i \ar[rr]^a \ar[dd]^b & & 1 \ar@/^/[ld]^h \ar@/_/[ld]_i \\
& \rho \ar@/^/[lu]^d \ar@/_/[lu]_e \ar[rd]^f & \\
0 \ar[ru]^g & & i+1 \ar[uu]^c}[/tex]
Next time, we will use these quivers to define superpotentials…
Comments