The footnote on page E. II.6 in Bourbaki’s 1970 edition of “Theorie des ensembles” reads
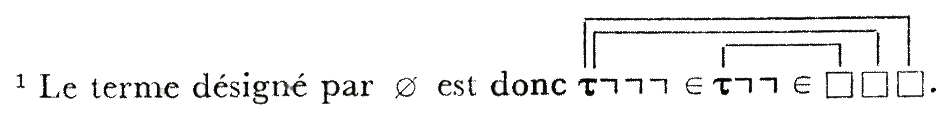
If this is completely obvious to you, stop reading now and start getting a life. For the rest of us, it took me quite some time before i was able to parse this formula, and when i finally did, it only added to my initial confusion.
Though the Bourbakis had a very preliminary version of their set-theory already out in 1939 (Fascicule des Resultats), the version as we know it now was published, chapter-wise, in the fifties: Chapters I and II in 1954, Chapter III in 1956 and finally Chapter IV in 1957.

In the first chapter they develop their version of logic, using ‘assemblages’ (assemblies) which are words of signs and letters, the signs being $\tau, \square, \vee, \neg, =, \in$ and $\supset$.
Of these, we have the familiar signs $\vee$ (or), $\neg$ (not), $=$ (equal to) and $\in$ (element of) and, three more exotic ones: $\tau$ (their symbol for the Hilbert operator $\varepsilon$), $\square$ a sort of wildcard variable bound by an occurrence of $\tau$ (the ‘links’ in the above scan) and $\supset$ for an ordered couple.
The connectives are written in front of the symbols they connect rather than between them, avoiding brackets, so far example $(x \in y) \vee (x=x)$ becomes $\vee \epsilon x y = x x$.
If $R$ is some assembly and $x$ a letter occurring in $R$, then the intende meaning of the *Hilbert-operator* $\tau_x(R)$ is ‘some $x$ for which $R$ is true if such a thing exists’. $\tau_x(R)$ is again an assembly constructed in three steps: (a) form the assembly $\tau R$, (b) link the starting $\tau$ to all occurrences of $x$ in $R$ and (c) replace those occurrences of $x$ by an occurrence of $\square$.
For MathJax reasons we will not try to draw links but rather give a linked $\tau$ and $\square$ the same subscript. So, for example, the claimed assembly for $\emptyset$ above reads
$\tau_y \neg \neg \neg \in \tau_x \neg \neg \in \square_x \square_y \square_y$
If $A$ and $B$ are assemblies and $x$ a letter occurring in $B$ then we denote by $(A | x)B$ the assembly obtained by replacing each occurrence of $x$ in $B$ by the assembly $A$. The upshot of this is that we can now write quantifiers as assemblies:
$(\exists x) R$ is the assembly $(\tau_x(R) | x)R$ and as $(\forall x) R$ is $\neg (\exists x) \neg R$ it becomes $\neg (\tau_x(\neg R) | x) \neg R$
Okay, let’s try to convert Bourbaki’s definition of the emptyset $\emptyset$ as ‘something that contains no element’, or formally $\tau_y((\forall x)(x \notin y))$, into an assembly.
– by definition of $\forall$ it becomes $\tau_y(\neg (\exists x)(\neg (x \notin y)))$
– write $\neg ( x \notin y)$ as the assembly $R= \neg \neg \in x \square_y$
– then by definition of $\exists$ we have to assemble $\tau_y \neg (\tau_x(R) | x) R$
– by construction $\tau_x(R) = \tau_x \neg \neg \in \square_x \square_y$
– using the description of $(A|x)B$ we finally indeed obtain $\tau_y \neg \neg \neg \in \tau_x \neg \neg \in \square_x \square_y \square_y$
But, can someone please explain what’s wrong with $\tau_y \neg \in \tau_x \in \square_x \square_y \square_y$ which is the assembly corresponding to $\tau_y(\neg (\exists x) (x \in y))$ which could equally well have been taken as defining the empty set and has a shorter assembly (length 8 and 3 links, compared to the one given of length 12 with 3 links).
Hair-splitting as this is, it will have dramatic implications when we will try to assemble Bourbaki’s definition of “1” another time.