the Bost-Connes Hecke algebra

As before, $\mathrm{\Gamma }$ is the subgroup of the rational linear group $G{L}_2(\mathbb{Q})$ consisting of the matrices

$\left[\begin{array}{cc}1& b\\ 0& a\end{array}\right]$ with $a\in {\mathbb{Q}}_{+}$ and ${\mathrm{\Gamma }}_0$ the subgroup of all matrices $\left[\begin{array}{cc}1& n\\ 0& 1\end{array}\right]$ with $n\in \mathbb{N}$. Last time, we have seen that the double coset space ${\mathrm{\Gamma }}_0\mathrm{\setminus }\mathrm{\Gamma }/{\mathrm{\Gamma }}_0$ can be identified with the set of all rational points in the fractal comb consisting of all couples $(a,b)$ with $a=\frac{m}{n}\in {\mathbb{Q}}_{+}$ and $b\in [0,\frac{1}{n})\cap \mathbb{Q}$

The blue spikes are at the positive natural numbers $a=1,2,3,\dots$. Over $a=1$ they correspond to the matrices $\left[\begin{array}{cc}1& \gamma \\ 0& 1\end{array}\right]$ with $\gamma \in [0,1)\cap \mathbb{Q}$ and as matrix-multiplication of such matrices corresponds to addition of the $\gamma$ we see that these cosets can be identified with the additive group $\mathbb{Q}/\mathbb{Z}$ (which will reappear at a later stage as the multiplicative group of all roots of unity).

The Bost-Connes Hecke algebra $\mathcal{H}=\mathcal{H}(\mathrm{\Gamma },{\mathrm{\Gamma }}_0)$ is the convolution algebra of all comlex valued functions with finite support on the double coset space ${\mathrm{\Gamma }}_0\mathrm{\setminus }\mathrm{\Gamma }/{\mathrm{\Gamma }}_0$. That is, as a vector space the algebra has as basis the functions $e_X$ with $X\in {\mathrm{\Gamma }}_0\mathrm{\setminus }\mathrm{\Gamma }/{\mathrm{\Gamma }}_0$ (that is, $X$ is a point of the fractal comb) and such that $e_X(X)=1$ and $e_X(Y)=0$ for all other double cosets $Y\ne X$. The algebra product on $\mathcal{H}$ is the convolution-product meaning that if $f,f^{\prime }$ are complex functions with finite support on the Bost-Connes space, then they can also be interpreted as ${\mathrm{\Gamma }}_0$-bi-invariant functions on the group $\mathrm{\Gamma }$ (for this just means that the function is constant on double cosets) and then $f\ast f^{\prime }$ is the function defined for all $\gamma \in \mathrm{\Gamma }$ by

$f\ast f^{\prime }(\gamma )=\sum _{\mu \in \mathrm{\Gamma }/{\mathrm{\Gamma }}_0}f(\mu )f^{\prime }({\mu }^{-1}\gamma )$

Last time we have seen that the coset-space $\mathrm{\Gamma }/{\mathrm{\Gamma }}_0$ can be represented by all rational points $(a,b)$ with $b<1$. At first sight, the sum above seems to be infinite, but, f and f’ are non-zero only at finitely many double cosets and we have see last time that ${\mathrm{\Gamma }}_0$ acts on one-sided cosets with finite orbits. Therefore, $f\ast f$ is a well-defined ${\mathrm{\Gamma }}_0$-bi-invariant function with finite support on the fractal comb ${\mathrm{\Gamma }}_0\mathrm{\setminus }\mathrm{\Gamma }/{\mathrm{\Gamma }}_0$. Further, observe that the unit element of $\mathcal{H}$ is the function corresponding to the identity matrix in $\mathrm{\Gamma }$.

Looking at fractal-comb picture it is obvious that the Bost-Connes Hecke algebra $\mathcal{H}$ is a huge object. Today, we will prove the surprising result that it can be generated by the functions corresponding to the tiny portion of the comb, shown below.

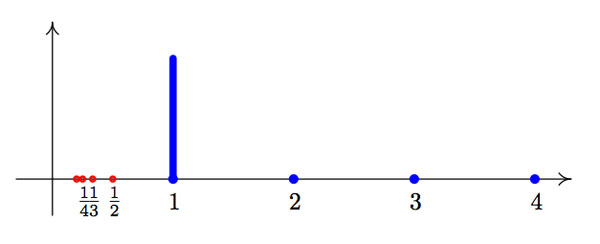
That is, we will show that $\mathcal{H}$ is generated by the functions $e(\gamma )$ corresponding to the double-coset $X_{\gamma }=\left[\begin{array}{cc}1& \gamma \\ 0& 1\end{array}\right]$ (the rational points of the blue line-segment over 1, or equivalently, the elements of the group $\mathbb{Q}/\mathbb{Z}$), together with the functions ${\varphi }_n$ corresponding to the double-coset $X_n=\left[\begin{array}{cc}1& 0\\ 0& n\end{array}\right]$ for all $n\in {\mathbb{N}}_{+}$ (the blue dots to the right in the picture) and the functions ${\varphi }_n^{\ast }$ corresponding to the double cosets $X_{1/n}=\left[\begin{array}{cc}1& 0\\ 0& \frac{1}{n}\end{array}\right]$ (the red dots to the left).

Take a point in the fractal comb $X=\left[\begin{array}{cc}1& \gamma \\ 0& \frac{m}{n}\end{array}\right]$ with $(m,n)=1$ and $\gamma \in [0,\frac{1}{n})\cap \mathbb{Q}\subset [0,1)\cap \mathbb{Q}$. Note that as $\gamma <\frac{1}{n}$ we have that $n\gamma <1$ and hence $e(n\gamma )$ is one of the (supposedly) generating functions described above.

Because $X=\left[\begin{array}{cc}1& \gamma \\ 0& \frac{m}{n}\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& m\end{array}\right]\left[\begin{array}{cc}1& n\gamma \\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& \frac{1}{n}\end{array}\right]=X_m{X}_{n\gamma }{X}_{1/n}$ we are aiming for a relation in the Hecke algebra ${\varphi }_m\ast e(n\gamma )\ast {\varphi }_n^{\ast }=e_X$. This is ‘almost’ true, except from a coefficient.

Let us prove first the equality of functions $e_X\ast {\varphi }_n=n{\varphi }_m\ast e(n\gamma )$. To do this we have to show that they have the same value for all points $Y\in {\mathrm{\Gamma }}_0\mathrm{\setminus }\mathrm{\Gamma }/{\mathrm{\Gamma }}_0$ in the fractal comb. Let us first study the function on the right hand side.

${\varphi }_m\ast e(n\gamma )=\sum _{g\in \mathrm{\Gamma }/{\mathrm{\Gamma }}_0}{\varphi }_m(g)e(n\gamma )(g^{-1}Y)$. Because $X_m{\mathrm{\Gamma }}_0$ is already a double coset (over $m$ we have a comb-spike of length one, so all rational points on it determine at the same time a one-sided and a double coset. Therefore, ${\varphi }_m(g)$ is zero unless $g=X_m$ and then the value is one.

Next, let us consider the function on the left-hand side. $e_X\ast {\varphi }_n(Y)=\sum _{g\in \mathrm{\Gamma }/{\mathrm{\Gamma }}_0}{e}_X(g){\varphi }_m(g^{-1}Y)$. We have to be a bit careful here as the double cosets over $a=\frac{m}{n}$ are different from the left cosets. Recall from last time that the left-cosets over a are given by all rational points of the form $(a,b)$ with $b<1$ whereas the double-cosets over a are represented by the rational points of the form $(a,b)$ with $b<\frac{1}{n}$ and hence the ${\mathrm{\Gamma }}_0$-orbits over a all consist of precisely n elements g.
That is, $e_X(g)$ is zero for all $g\in \mathrm{\Gamma }/{\mathrm{\Gamma }}_0$ except when g is one of the following matrices

$g\in \left[\begin{array}{cc}1& \gamma \\ 0& \frac{m}{n}\end{array}\right],\left[\begin{array}{cc}1& \gamma +\frac{1}{n}\\ 0& \frac{m}{n}\end{array}\right],\left[\begin{array}{cc}1& \gamma +\frac{2}{n}\\ 0& \frac{m}{n}\end{array}\right],\dots ,\left[\begin{array}{cc}1& \gamma +\frac{n-1}{n}\\ 0& \frac{m}{n}\end{array}\right]$

Further, ${\varphi }_n(g^{-1}Y)$ is zero unless $g^{-1}Y\in {\mathrm{\Gamma }}_0\left[\begin{array}{cc}1& 0\\ 0& n\end{array}\right]{\mathrm{\Gamma }}_0$, or equivalently, that $Y\in {\mathrm{\Gamma }}_{0}g{\mathrm{\Gamma }}_0\left[\begin{array}{cc}1& 0\\ 0& n\end{array}\right]{\mathrm{\Gamma }}_0={\mathrm{\Gamma }}_{0}g\left[\begin{array}{cc}1& 0\\ 0& n\end{array}\right]{\mathrm{\Gamma }}_0$ and for each of the choices for g we have that

$\left[\begin{array}{cc}1& \gamma +\frac{k}{n}\\ 0& \frac{m}{n}\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& n\end{array}\right]=\left[\begin{array}{cc}1& n\gamma +k\\ 0& m\end{array}\right]\sim \left[\begin{array}{cc}1& n\gamma \\ 0& m\end{array}\right]$

Therefore, the function $e_X\ast {\varphi }_n$ is zero at every point of the fractal comb unless at $\left[\begin{array}{cc}1& n\gamma \\ 0& m\end{array}\right]$ where it is equal to $n$. This proves the claimed identity of functions and as one verifies easily that ${\varphi }_n^{\ast }\ast {\varphi }_n=1$, it follows that all base vectors $e_X$ of $\mathcal{H}$ can be expressed in the claimed generators

$e_X=n{\varphi }_m\ast e(n\gamma )\ast {\varphi }_n^{\ast }$

Bost and Connes use slightly different generators, namely with ${\mu }_n=\frac{1}{\sqrt{n}}{\varphi }_n$ and ${\mu }_n^{\ast }=\sqrt{n}{\varphi }_n^{\ast }$ in order to have all relations among the generators being defined over $\mathbb{Q}$ (as we will see another time). This will be important later on to have an action of the cyclotomic Galois group $Gal({\mathbb{Q}}^{cycl}/\mathbb{Q})$ on certain representations of $\mathcal{H}$.