Skip to content →

Tag: topology

mathematics & unhappiness

Published October 23, 2006 by lieven

Sociologists are a constant source of enlightenment as CNN keeps reminding

Kids who are turned
off by math often say they don’t enjoy it, they aren’t good
at it and they see little point in it. Who knew that could be a formula
for success?
The nations with the best scores have the
least happy, least confident math students, says a study by the
Brookings Institution’s Brown Center on Education Policy.
Countries reporting higher levels of enjoyment and confidence
among math students don’t do as well in the subject, the study
suggests.
The eighth-grade results reflected a common
pattern: The 10 nations whose students enjoyed math the most all scored
below average. The bottom 10 nations on the enjoyment scale all
excelled.

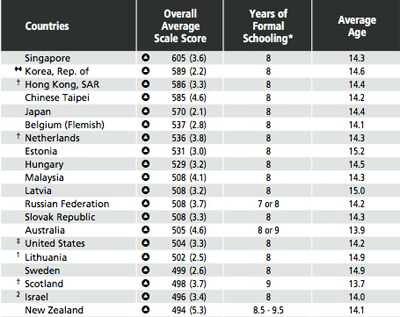
As this study is based on the 2003 Trends in International
Mathematics and Science Studies and as “we” scored best
of all western countries
this
probably explains all the unhappy faces in my first-year class on group
theory. However, they seemed quite happy the first few weeks.
Fortunately, this is proof, at least according to the mountain of wisdom, that I’m on the right track

If too many students are too happy in the math
classes, be sure that it is simply because not much is expected from
them. It can’t be otherwise. If teaching of mathematics is
efficient, it is almost guaranteed that a large group or a majority must
dislike the math classes. Mathematics is hard and if it is not hard, it
is not mathematics.

Right on! But then, why is
it that people willing to study maths enter university in a happy mood?
Oh, I get it, yes, it must be because in secondary school not much was
expected of them! Ouf! my entire world is consistent once again.
But then, hey wait, the next big thing that’s inevitably going to
happen is that in 2007 “we” will be tumbling down this world
ranking! And, believe it or not, that is precisely what
all my colleagues are eagerly awaiting to happen. Most of us are willing
to bet our annual income on it. Belgium was among the first countries to
embrace in the sixties-early seventies what was then called
“modern mathematics’ (you know: Venn-diagrams, sets,
topology, categories (mind you, just categories not the n-stuff ) etc.) Whole
generations of promising Belgian math students were able in the late
70ties, 80ties and early 90ties to do what they did mainly because of
this (in spite of graduating from ‘just’ a Belgian
university, only some of which make it barely in the times top 100 ). But
then, in the ’90ties politicians decided that mathematics had to
be sexed-up, only the kind of mathematics that one might recognize in
everyday life was allowed to be taught. For once, I have to
agree with motl.

Also, the attempts to connect mathematics with
the daily life are nothing else than a form of lowering of the
standards. They are a method to make mathematics more attractive for
those who like to talk even if they don’t know what they’re
talking about. They are a method to include mathematics between the
social and subjective sciences. They give a wiggle room to transform
happiness, confidence, common sense, and a charming personality into
good grades.

Indeed, the major problem we are
facing today in first year classes is that most students have no formal
training at all! An example : last week I did a test after three weeks
of working with groups. One of the more silly questions was to ask them
for precise definitions of very basic concepts (groups, subgroups,
cyclic groups, cosets, order of an element) : just 5 out of 44 were able
to do this! Most of them haven’t heard of sets at all. It seems
that some time ago it was decided that sets no longer had a place in
secondary school, so just some of them had at least a few lessons on
sets in primary school (you know the kind (probably you won’t but
anyway) : put all the green large triangles in the correct place in the
Venn diagram and that sort of things). Now, it seems that politicians
have decided that there is no longer a place for sets in primary schools
either! (And if we complain about this drastic lowering of
math-standards in schools, we are thrown back at us this excellent 2003
international result, so the only hope left for us is that we will fall
down dramatically in the 2007 test.) Mind you, they still give
you an excellent math-education in Belgian primary and secondary schools
provided you want to end up as an applied mathematician or (even worse)
a statistician. But I think that we, pure mathematicians, should
seriously consider recruiting students straight from Kindergarten!

Leave a Comment

Krull & Paris

Published September 5, 2006 by lieven

The
Category-Cafe ran an interesting post The history of n-categories
claiming that “mathematicians’ histories are largely
‘Royal-road-to-me’ accounts”

To my mind a key
difference is the historians’ emphasis in their histories that things
could have turned out very differently, while the mathematicians tend to
tell a story where we learn how the present has emerged out of the past,
giving the impression that things were always going to turn out not very
dissimilarly to the way they have, even if in retrospect the course was
quite tortuous.

Over the last weeks I’ve been writing up
the notes of a course on ‘Elementary Algebraic Geometry’ that I’ll
be teaching this year in Bach3. These notes are split into three
historical periods more or less corresponding to major conceptual leaps
in the subject : (1890-1920) ideals in polynomial rings (1920-1950)
intrinsic definitions using the coordinate ring (1950-1970) scheme
theory. Whereas it is clear to take Hilbert&Noether as the leading
figures of the first period and Serre&Grothendieck as those of the
last, the situation for the middle period is less clear to me. At
first I went for the widely accepted story, as for example phrased by Miles Reid in the
Final Comments to his Undergraduate Algebraic Geometry course.

…
rigorous foundations for algebraic geometry were laid in the 1920s and
1930s by van der Waerden, Zariski and Weil (van der Waerden’s
contribution is often suppressed, apparently because a number of
mathematicians of the immediate post-war period, including some of the
leading algebraic geometers, considered him a Nazi collaborator).

But then I read The Rising Sea: Grothendieck
on simplicity and generality I by Colin McLarty and stumbled upon
the following paragraph

From Emmy Noether’s viewpoint,
then, it was natural to look at prime ideals instead of classical and
generic pointsโ€šร„รฎor, as we would more likely say today, to identify
points with prime ideals. Her associate Wolfgang Krull did this. He gave
a lecture in Paris before the Second World War on algebraic geometry
taking all prime ideals as points, and using a Zariski topology (for
which see any current textbook on algebraic geometry). He did this over
any ring, not only polynomial rings like C[x, y]. The generality was
obvious from the Noether viewpoint, since all the properties needed for
the definition are common to all rings. The expert audience laughed at
him and he abandoned the idea.

The story seems to be
due to Jurgen Neukirch’s ‘Erinnerungen an Wolfgang Krull’
published in ‘Wolfgang Krull : Gesammelte Abhandlungen’ (P.
Ribenboim, editor) but as our library does not have this book I would
welcome any additional information such as : when did Krull give this
talk in Paris? what was its precise content? did he introduce the prime
spectrum in it? and related to this : when and where did Zariski
introduce ‘his’ topology? Answers anyone?

Leave a Comment

noncommutative topology (4)

Published February 9, 2006 by lieven

For a
qurve (aka formally smooth algebra) A a *block* is a (possibly infinite
dimensional over the basefield) left A-module X such that its
endomorphism algebra $D = End_A(X)$ is a division algebra and X
(considered as a right D-module) is finite dimensional over D. If a
block X is finite dimensional over the basefield, we call it a *brick*
(aka a *Schur representation*). We want to endow the set of all blocks
with a topology and look at the induced topology on the subset of
bricks. It is an old result due to Claus Ringel
that there is a natural one-to-one correspondence between blocks of A
and algebra epimorphisms (in the categorical sense meaning that identify
equality of morphisms to another algebra) $A \rightarrow M_n(D) =
End_D(X_D)$. This result is important as it allows us to define a
partial order on teh set of all A-blocks via the notion of
*specialization*. If X and Y are two A-blocks with corresponding
epimorphisms $A \rightarrow M_n(D),~A \rightarrow M_m(E)$ we say that Y
is a specialization of X and we denote $X \leq Y$ provided there is an
epimorphism $A \rightarrow B$ making the diagram below commute

$\xymatrix{& M_n(D) \\\ A \ar[ru] \ar[r] \ar[rd] & B \ar[u]^i
\ar[d]^p \\\ & M_m(E)} $

where i is an inclusion and p is a
onto. This partial ordering was studied by Paul Cohn, George Bergman and
Aidan Schofield who use
the partial order to define the _closed subsets_ of blocks to be
those closed under specialization.

There are two important
constructions of A-blocks for a qurve A. One is Aidan’s construction of
a universal localization wrt. a *Sylvester rank function* (and which
should be of use in noncommutative rationality problems), the other
comes from invariant theory and is related to Markus Reineke’s monoid in
the special case when A is the path algebra of a quiver. Let X be a
GL(n)-closed irreducible subvariety of an irreducible component of
n-dimensional A-representations such that X contains a brick (and hence
a Zariski open subset of bricks), then taking PGL(n)-equivariant maps
from X to $M_n(\mathbb{C})$ determines a block (by inverting all central
elements). Now, take a *sensible* topology on the set of all A-bricks.
I would go for defining as the open wrt. a block X, the set of all
A-bricks which become simples after extending by the epimorphism
determined by a block Y such that $Y \leq X$. (note that this seems to
be different from the topology coming from the partial ordering…).
Still, wrt. this topology one can then again define a *noncommutative
topology* on the Abelian category $\mathbf{rep}~A$ of all finite
dimensional A-representations
but this time using filtrations with successive quotients being bricks
rather than simples.

Leave a Comment