Tag: simples

Weil descent

Published January 9, 2008 by lieven

A classic Andre Weil-tale is his narrow escape from being shot as a Russian spy

The war was a disaster for Weil who was a conscientious objector and so wished to avoid military service. He fled to Finland, to visit Rolf Nevanlinna, as soon as war was declared. This was an attempt to avoid being forced into the army, but it was not a simple matter to escape from the war in Europe at this time. Weil was arrested in Finland and when letters in Russian were found in his room (they were actually from Pontryagin describing mathematical research) things looked pretty black. One day Nevanlinna was told that they were about to execute Weil as a spy, and he was able to persuade the authorities to deport Weil instead.

However, Weil’s wikipedia entry calls this a story too good to be true, and continues

In 1992, the Finnish mathematician Osmo Pekonen went to the archives to check the facts. Based on the documents, he established that Weil was not really going to be shot, even if he was under arrest, and that Nevanlinna probably didn’t do – and didn’t need to do – anything to save him. Pekonen published a paper on this with an afterword by Andre Weil himself. Nevanlinna’s motivation for concocting such a story of himself as the rescuer of a famous Jewish mathematician probably was the fact that he had been a Nazi sympathizer during the war. The story also appears in Nevanlinna’s autobiography, published in Finnish, but the dates don’t match with real events at all. It is true, however, that Nevanlinna housed Weil in the summer of 1939 at his summer residence Korkee at Lohja in Finland – and offered Hitler’s Mein Kampf as bedside reading.

This old spy-story gets a recent twist now that it turns out that Weil’s descent theory of tori has applications to cryptography. So far, I haven’t really defined what tori are, so let us start with some basics.

The simplest (and archetypical) example of an algebraic torus is the multiplicative group(scheme) $G_{m}$ over a finite field $F_{q}$ which is the affine variety

$V (x y - 1) \subset A_{F_{q}}^{2}$ . that is, the $F_{q}$ points of $G_{m}$ are precisely the couples $(x, \frac{1}{x}) : x \in F_{q}^{*}$ and so are in one-to-one correspondence with the non-zero elements of $F_{q}$ . The coordinate ring of this variety is the ring of Laurant polynomials $F_{q} [x, x^{- 1}]$ and the fact that multiplication induces a group-structure on the points of the variety can be rephrased by saying that this coordinate ring is a Hopf algebra which is just the Hopf structure on the group-algebra $F_{q} [Z] = F_{q} [x, x^{- 1}]$ . This is the first indication of a connection between tori defined over $F_{q}$ and lattices (that is free $Z$ -modules with an action of the Galois group $G a l ({\overset{―}{F}}_{q} / F_{q})$ . In this correspondence, the multiplicative group scheme $G_{m}$ corresponds to $Z$ with the trivial action.

Now take a field extension $F_{q} \subset F_{q^{n}}$ , is there an affine variety, defined over $F_{q}$ whose $F_{q}$ -points are precisely the invertible elements $F_{q^{n}}^{*}$ ? Sure! Just take the multiplicative group over $F_{q^{n}}$ and write the elements x and y as $x = x_{1} + x_{2} a_{2} + \dots + x_{n} a_{n}$ (and a similar expression for y with $1, a_{2}, \dots, a_{n}$ being a basis of $F_{q^{n}} / F_{q}$ and write the defning equation $x y - 1$ out, also with respect to this basis and this will then give you the equations of the desired variety, which is usually denoted by $R_{F_{q^{n}} / F_{q}}^{1} G_{m}$ and called the Weil restriction of scalars torus.

A concrete example? Take $F_{9} = F_{3} (\sqrt{- 1})$ and write $x = x_{1} + x_{2} \sqrt{- 1}$ and $y = y_{1} + y_{2} \sqrt{- 1}$ , then the defining equation $x y - 1$ becomes

$(x_{1} y_{1} - x_{2} y_{2}) + (x_{1} y_{2} - x_{2} y_{1}) \sqrt{- 1} = 1$

whence $R_{F_{9} / F_{3}}^{1} = V (x_{1} y_{1} - x_{2} y_{2} - 1, x_{1} y_{2} - x_{2} y_{1}) \subset A_{F_{3}}^{4}$ , the intersection of two quadratic hypersurfaces in 4-dimensional space.

Why do we call $R^{1} G_{m}$ a _torus_? Well, as with any variety defined over $F_{q}$ we can also look at its points over a field-extension, for example over the algebraic closure ${\overset{―}{F}}_{q}$ and then it is easy to see that

$R_{F_{q^{n}} / F_{q}}^{1} G_{m} ({\overset{―}{F}}_{q}) = {\overset{―}{F}}_{q}^{*} \times \dots \times {\overset{―}{F}}_{q}^{*}$ (n copies)

and such algebraic groups are called tori. (To understand terminology, the compact group corresponding to $C^{*} \times C^{*}$ is $U_{1} \times U_{1} = S^{1} \times S^{1}$ , so a torus).

In fact, it is already the case that the $F_{q^{n}}$ points of the restriction of scalar torus are $F_{q^{n}}^{*} \times \dots \times F_{q^{n}}^{*}$ and therefore we call this field a splitting field of the torus.

This is the general definition of an algebraic torus : a torus T over $F_{q}$ is an affine group scheme over $F_{q}$ such that, if we extend scalars to the algebraic closure (and then it already holds for a finite extension) we get an isomorphism of affine group schemes

$T \times_{F_{q}} {\overset{―}{F}}_{q} = {\overset{―}{F}}_{q}^{*} \times \dots \times {\overset{―}{F}}_{q}^{*} = ({\overset{―}{F}}_{q}^{*})^{n}$

in which case we call T a torus of dimension n. Clearly, the Galois group $G a l ({\overset{―}{F}}_{q}^{*} / F_{q})$ acts on the left hand side in such a way that we recover $T$ as the orbit space for this action.

Hence, anther way to phrase this is to say that an algebraic torus is the Weil descent of an action of the Galois group on the algebraic group ${\overset{―}{F}}_{q}^{*} \times \dots \times {\overset{―}{F}}_{q}^{*}$ .

Of course we can also rephrase this is more algebraic terms by looking at the coordinate rings. The coordinate ring of the algebraic group $({\overset{―}{F}}_{q}^{*})^{n}$ is the group-algebra of the rank n lattice $Z^{n} = Z \oplus \dots \oplus Z$ (the free Abelian group of rank n), that is,
${\overset{―}{F}}_{q} [Z^{n}]$ . Now the Galois group acts both on the field ${\overset{―}{F}}_{q}$ as on the lattice $Z^{n}$ coming from the action of the Galois group on the extended torus $T \times_{F_{q}} {\overset{―}{F}}_{q}$ . In fact, it is best to denote this specific action on $Z^{n}$ by $T^{*}$ and call $T^{*}$ the character group of $T$ . Now, we recover the coordinate ring of the $F_{q}$ -torus $T$ as the ring of invariants

$F_{q} [T] = {\overset{―}{F}}_{q} [T^{*}]^{G a l ({\overset{―}{F}}_{q} / F_{q})}$

Hence, the restriction of scalars torus $R_{F_{q^{n}} / F_{q}}^{1} G_{m}$ is an n-dimensional torus over $F_{q}$ and its corresponding character group is the free Abelian group of rank n which can be written as $Z [x] / (x^{n} - 1) = Z 1 \oplus Z x \oplus \dots \oplus Z x^{n - 1}$ and where the action of the cyclic Galois group $G a l (F_{q^{n}} / F_{q}) = C_{n} = ⟨ σ ⟩$ s such that the generator $σ$ as as multiplication by $x$ . That is, in this case the character group is a permutation lattice meaning that the $Z$ -module has a basis which is permuted under the action of the Galois group. Next time we will encounter more difficult tori sich as the crypto-torus $T_{n}$ .

working archive plugin, please!

Published January 8, 2008 by lieven

Over the last two weeks Ive ported all old neverendingbooks-post from the last 4 years to a nearly readable format. Some tiny problems remain : a few TeX-heavy old posts are still in $\dots$ format rather than LaTeXrender-compatible (but Ill fix this soon), a few links may turn out to be dead (still have to check out those), TheLibrary-project links do not exist at the moment (have to decide whether to revive the project or to start a similar idea afresh), some other techie-things such as FoaF-stuff will be updated/expanded soon, et. etc. (and still have to port some 20 odd posts).

Anyway, the good news being that we went from about 40 posts since last july to over 310 posts, all open to the internal Search engine. Having all this stuff online is only useful if one can browse through it easily, so I wanted to install a proper up-to-date archive-plugin…

The current theme Redoable has build-in support for the Extended Live Archives v0.10beta-r18 plugin which would be ideal if I could get it installed… Im not the total newbie in installing WordPress-plugins and Ive read all the documentation and the support-forum and chmodded whathever I felt like chmodding, but still no success… If you know how to kick it into caching the necessary files, please drop a comment!

The next alternative Ive tried was the AWSOM Archive Version 1.2.3 plugin which gave me a pull-down menu just under the title-bar but not much seems to happen when using bloody Safari (Flock was OK though). Maybe Ill give it another go…

UPDATE (jan. 9th) : The AWSOM Archive seems to be working fine with the Redoable theme when custom installed in the footer. So, there is now a pulldown-menu at the bottom of the page.

**UPDATE (jan. 12th) : Ive installed the new version 1.3 of AWSOM Archive and it works from the default position **

At a loss I opted in the end for the simplest (though not the most aesthetic) plugin : Justin Blanton’s Smart Archives. This provides a year-month scheme at the top followed by a reverse ordered list of all months and titles of posts and is available as the arXiv neverendingbooks link available also from the sidebar (up, second link). I hope it will help you not to get too lost on this site…

Suggestions for a working-from-the-box WordPress Archive plugin, anyone???

the modular group and superpotentials (1)

Published December 26, 2007 by lieven

Here I will go over the last post at a more leisurely pace, focussing on a couple of far more trivial examples. Here’s the goal : we want to assign a quiver-superpotential to any subgroup of finite index of the modular group. So fix such a subgroup $Γ^{'}$ of the modular group $Γ = P S L_{2} (Z)$ and consider the associated permutation representation of $Γ$ on the left-cosets $Γ / Γ^{'}$ . As $Γ ≃ C_{2} * C_{3}$ this representation is determined by the action of the order 2 and order 3 generators of the modular group. There are a number of combinatorial gadgets to control the subgroup $Γ^{'}$ and the associated permutation representation : (generalized) Farey symbols and dessins d’enfants.

Recall that the modular group acts on the upper-halfplane (the ‘hyperbolic plane’) by Moebius transformations, so to any subgroup $Γ^{'}$ we can associate a fundamental domain for its restricted action. The dessins and the Farey symbols give us a particular choice of these fundamental domains. Let us consider the two most trivial subgroups of all : the modular group itself (so $Γ / Γ$ is just one element and therefore the associated permutation representation is just the trivial representation) and the unique index two subgroup $Γ_{2}$ (so there are two cosets $Γ / Γ_{2}$ and the order 2 generator interchanges these two while the order 3 generator acts trivially on them). The fundamental domains of $Γ$ (left) and $Γ_{2}$ (right) are depicted below

In both cases the fundamental domain is bounded by the thick black (hyperbolic) edges. The left-domain consists of two hyperbolic triangles (the upper domain has $\infty$ as the third vertex) and the right-domain has 4 triangles. In general, if the subgroup $Γ^{'}$ has index n, then its fundamental domain will consist of $2 n$ hyperbolic triangles. Note that these triangles are part of the Dedekind tessellation so really depict the action of $P G L_{2} (Z$ and any $Γ$ -hyperbolic triangle consists of one black and one white triangle in Dedekind’s coloring. We will indicate the color of a triangle by a black circle if the corresponding triangle is black. Of course, the bounding edges of the fundamental domain need to be identified and the Farey symbol is a notation device to clarify this. The Farey symbols of the above domains are
[tex]\xymatrix{\infty \ar@{-}[r]_{\circ} & 0 \ar@{-}[r]_{\bullet} & \infty}[/tex] and [tex]\xymatrix{\infty \ar@{-}[r]_{\bullet} & 0 \ar@{-}[r]_{\bullet} & \infty}[/tex] respectively. In both cases this indicates that the two bounding edges on the left are to be identified as are the two bounding edges on the right (so, in particular, after identification $\infty$ coincides with $0$ ). Hence, after identification, the $Γ$ domain consists of two triangles on the vertices $0, i, ρ$ (where $ρ = e^{2 π i} 6$ ) (the blue dots) sharing all three edges, the $Γ_{2}$ domain consists of 4 triangles on the 4 vertices $0, i, ρ, ρ^{2}$ (the blue dots). In general we have three types of vertices : cusps (such as 0 or $\infty$ ), even vertices (such as $i$ where there are 4 hyperbolic edges in the Dedekind tessellation) and odd vertices (such as $ρ$ and $ρ^{2}$ where there are 6 hyperbolic edges in the tessellation).

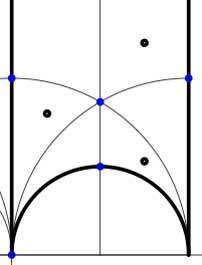
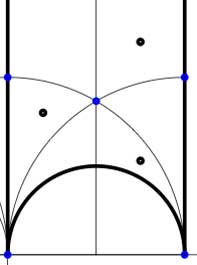Another combinatorial gadget assigned to the fundamental domain is the cuboid tree diagram or dessin. It consists of all odd and even vertices on the boundary of the domain, together with all odd and even vertices in the interior. These vertices are then connected with the hyperbolic edges connecting them. If we color the even vertices red and the odds blue we have the indicated dessins for our two examples (the green pictures). An half-edge is an edge connecting a red and a blue vertex in the dessin and we number all half-edges. So, the $Γ$ -dessin has 1 half-edge whereas the $Γ_{2}$ -dessin has two (in general, the number of these half-edges is equal to the index of the subgroup). Observe also that every triangle has exactly one half-edge as one of its three edges. The dessin gives all information to calculate the permutation representation on the coset-set $Γ / Γ^{'}$ : the action of the order 2 generator of $Γ$ is given by taking for each internal red vertex the two-cycle $(a, b)$ where a and b are the numbers of the two half-edges connected to the red vertex and the action of the order 3 generator is given by taking for every internal blue vertex the three cycle $(c, d, e)$ where c, d and e are the numbers of the three half-edges connected to the blue vertex in counter-clockwise ordering. Our two examples above are a bit too simplistic to view this in action. There are no internal blue vertices, so the action of the order 3 generator is trivial in both cases. For $Γ$ there is also no red internal vertex, whence this is indeed the trivial representation whereas for $Γ_{2}$ there is one internal red vertex, so the action of the order 2 generator is given by $(1, 2)$ , which is indeed the representation representation on $Γ / Γ_{2}$ . In general, if the index of the subgroup $Γ^{'}$ is n, then we call the subgroup of the symmetric group on n letters $S_{n}$ generated by the action-elements of the order 2 and order 3 generator the monodromy group of the permutation representation (or of the subgroup). In the trivial cases here, the monodromy groups are the trivial group (for $Γ$ ) and $C_{2}$ (for $Γ_{2}$ ).

As a safety-check let us work out all these concepts in the next simplest examples, those of some subgroups of index 3. Consider the Farey symbols

[tex]\xymatrix{\infty \ar@{-}[r]_{\circ} & 0 \ar@{-}[r]_{\circ} & 1 \ar@{-}[r]_{\circ} & \infty}[/tex] and
[tex]\xymatrix{\infty \ar@{-}[r]_{\circ} & 0 \ar@{-}[r]_{1} & 1 \ar@{-}[r]_{1} & \infty}[/tex]

In these cases the fundamental domain consists of 6 triangles with the indicated vertices (the blue dots). The distinction between the two is that in the first case, one identifies the two edges of the left, resp. bottom, resp. right boundary (so, in particular, 0,1 and $\infty$ are identified) whereas in the second one identifies the two edges of the left boundary and identifies the edges of the bottom with those of the right boundary (here, 0 is identified only with $\infty$ but also $1 + i$ is indetified with $\frac{1}{2} + \frac{1}{2} i$ ).

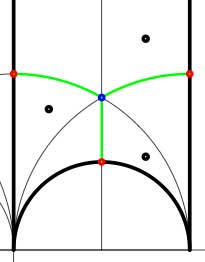In both cases the dessin seems to be the same (and given by the picture on the right). However, in the first case all three red vertices are distinct hence there are no internal red vertices in this case whereas in the second case we should identify the bottom and right-hand red vertex which then becomes an internal red vertex of the dessin!

Hence, if we order the three green half-edges 1,2,3 starting with the bottom one and counting counter-clockwise we see that in both cases the action of the order 3-generator of $Γ$ is given by the 3-cycle $(1, 2, 3)$ . The action of the order 2-generator is trivial in the first case, while given by the 2-cycle $(1, 2)$ in the second case. Therefore, the monodromy group is the cylic group $C_{3}$ in the first case and is the symmetric group $S_{3}$ in the second case.

Next time we will associate a quiver to these vertices and triangles as well as a cubic superpotential which will then allow us to define a noncommutative algebra associated to any subgroup of the modular group. The monodromy group of the situation will then reappear as a group of algebra-automorphisms of this noncommutative algebra!