Riemann – Page 11 – neverendingbooks

Modular quilts and cuboid tree diagrams

Published June 25, 2007 by lieven

Conjugacy classes of finite index subgroups of the modular group $Γ = P S L_{2} (Z)$ are determined by a combinatorial gadget : a modular quilt. By this we mean a finite connected graph drawn on a Riemann surface such that its vertices are either black or white. Moreover, every edge in the graph connects a black to a white vertex and the valency (that is, the number of edges incodent to a vertex) of a black vertex is either 1 or 2, that of a white vertex is either 1 or 3. Finally, for every white vertex of valency 3, there is a prescribed cyclic order on the edges incident to it.

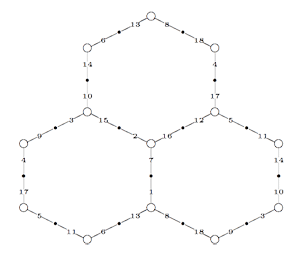
On the left a modular quilt consisting of 18 numbered edges (some vertices and edges re-appear) which gives a honeycomb tiling on a torus. All white vertices have valency 3 and the order of the edges is given by walking around a point in counterclockwise direction. For example, the order of the edges at the top left vertex (which re-appears at the middle right vertex) can be represented by the 3-cycle (6,11,14), that around the central vertex gives the 3-cycle (2,7,16).

Hexagonal Moonshine (1)

Published June 18, 2007 by lieven

Over at the Arcadian Functor, Kea is continuing her series of blog posts on M-theory (the M is supposed to mean either Monad or Motif). A recurrent motif in them is the hexagon and now I notice hexagons popping up everywhere. I will explain some of these observations here in detail, hoping that someone, more in tune with recent technology, may have a use for them.

The three string braid group $B_{3}$ is expected to play a crucial role in understanding monstrous moonshine so we should know more about it, for example about its finite dimensional representations. Now, _M geometry_ is pretty good at classifying finite dimensional representations provided the algebra is “smooth” which imples that for every natural number n the variety ${rep}_{n} A$ of n-dimensional representations of A is a manifold. Unfortunately, the group algebra $A = C B_{3}$ of the three string braid group is singular as we will see in a moment and the hunt for singularities in low dimensional representation varieties will reveal hexagons.

NeverEndingBooks-general

Published June 12, 2007 by lieven

Here a list of pdf-files of NeverEndingBooks-posts on general topics, in reverse chronological order.

Tag: Riemann

Modular quilts and cuboid tree diagrams

Hexagonal Moonshine (1)

NeverEndingBooks-general