Skip to content →

Tag: puzzle

sudoku mania

Published June 26, 2005 by lieven


I never pay
much attention to the crossword-puzzle page of our regular newspaper DeMorgen. I did notice that they
started a new sort of puzzle a few weeks ago but figured it had to be
some bingo-like stupidity. It wasn’t until last friday that I had a
look at the simple set of rules and I was immediately addicted (as I am
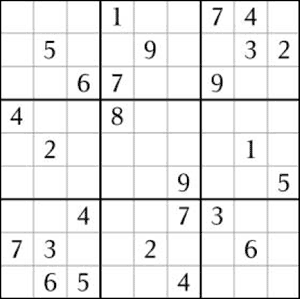
mostly when the rules are simple enough!). One is given a 9×9 grid
filled with numbers from 1 to 9. You have to fill in the full grid
making sure that each number appears just once on each _horizontal
line_, on each _vertical line_ and in each
of the indicated 3×3 subgrids!

It is amazing how quickly one learns
the basic tricks to solve such _sudoku_s. At first, one plays by
the horizontal-vertical rule trying to find forbidden positions for
certain numbers but rapidly one fails to make more progress. Then, it
takes a while before you realize that the empty squares on a given line
in a 3×3 subgrid cannot be filled with any of the numbers already
present in the 3×3 subgrid. Easy enough, but it takes your
sudoku-experience to the next level. Anther simple trick I found useful
it to keep track how many times (from 0 to 9) you have already filled
out a given number. If it is 9, you may as well forget about this number
for elimination purposes and if it is 0 it will be hard to use it.
Optimal numbers to use are those that are already 4 to 6 times on the
board. And so on, and so on.

After having traced all back-copies
of the newspaper I ran out of sudokus but fortunately there is a
neverending (sic!) supply of them on the web. For example, try out the
archive of Daily
Sudoku, and there are plenty of similar sites as, no doubt, you’ll
find by Googling.

An intruiging fact I learned from my newspaper
is that there are exactly 6,670,903,752,021,072,936,960 different
filled-out Sudoku grids. You then think : this should be easy enough to
prove using some simple combi- and factorials until you give this number
to Mathematica to factor it and find that it is

$2^{20} \\times
3^{8} \\times 5 \\times 7 \\times 27704267971$

and hence has a
pretty big unexplained prime factor! This fact needed clarification, so
a little bit later I found this Sodoku
players forum page and shortly afterwards an excellent (really
excellent) Wikipedia on
Sudoku. There is enough material on that page to keep you interested
for a while (e.g. the fact that nxn sudoku is NP-complete).

Leave a Comment

snortGO

Published December 17, 2004 by lieven

Before I'm bogged down by the changes let me
return to the snortGO
puzzle. Recall that in snortGO black and white take
turns in placing a Go-stone on the board respecting the rule that no
stones of opposite colour may be adjacent. Javier is right that snortGo
with an empty starting board having an odd number of rows and columns is
a first player's win (place your first stone on the central spot and
respond to your opponent's moves by reflecting them along the
center).
Still, one can compose realistic end-game problems (as
in the previous snortGo post where the problem was : prove that the position is a first
player's win and indicate a winning move for both black and white).
To start the analysis let us remove all spots which are unavailable for
both players (as depicted in the top picture). Some of the remaining
spots are available to just one player (the central free spots and the
two in the top left corner). One counts that black has 5 such central
spots and white 4 (including the top left corner). So, all the genuine
action is happening in the three remaining corner regions for which one
can calculate the exact value following the rules of combinatorial game
theory where bLack is playing Left and white Right (so the free
spots for black add up to +5 whereas those for white add up to -4). It
is pretty easy to work out the exact values of the corner subgames

To find the value of the total game we have to sum up these
values which can either be done by hand (use this and this to get
started and use the inductive rule $G+H = \\{ G^L+H,G+H^L \\vert
G^R+H,G+H^R \\}$) or using combinatorial game suite to
verify that this sum is equal to $\\{ \\{ 3 \\vert 2 \\} \\vert -1 \\}$
which is a fuzzy game (that is, confused with zero or a first
player's win). To find the actual winning moves just try out the
Left (bLack) and Right (white) options in the corner games to find out
that there is a unique winning move for white and there are just 2
winning moves for bLack, all indicated in the pictures below.

Leave a Comment

quintominal dodecahedra

Published December 15, 2004 by lieven


A _quintomino_ is a regular pentagon having all its sides
colored by five different colours. Two quintominoes are the same if they
can be transformed into each other by a symmetry of the pentagon (that
is, a cyclic rotation or a flip of the two faces). It is easy to see
that there are exactly 12 different quintominoes. On the other hand,
there are also exactly 12 pentagonal faces of a dodecahedron
whence the puzzling question whether the 12 quintominoes can be joined
together (colours mathching) into a dodecahedron.
According to
the Dictionnaire de
mathematiques recreatives this can be done and John Conway found 3
basic solutions in 1959. These 3 solutions can be found from the
diagrams below, taken from page 921 of the reprinted Winning Ways for your Mathematical
Plays (volume 4) where they are called _the_ three
quintominal dodecahedra giving the impression that there are just 3
solutions to the puzzle (up to symmetries of the dodecahedron). Here are
the 3 Conway solutions

One projects the dodecahedron down from the top face which is
supposed to be the quintomino where the five colours red (1), blue (2),
yellow (3), green (4) and black(5) are ordered to form the quintomino of
type A=12345. Using the other quintomino-codes it is then easy to work
out how the quintominoes fit together to form a coloured dodecahedron.

In preparing to explain this puzzle for my geometry-101 course I
spend a couple of hours working out a possible method to prove that
these are indeed the only three solutions. The method is simple : take
one or two of the bottom pentagons and fill then with mathching
quintominoes, then these more or less fix all the other sides and
usually one quickly runs into a contradiction.
However, along the
way I found one case (see top picture) which seems to be a _new_
quintominal dodecahedron. It can't be one of the three Conway-types
as the central quintomino is of type F. Possibly I did something wrong
(but what?) or there are just more solutions and Conway stopped after
finding the first three of them…
Update (with help from
Michel Van den Bergh) Here is an elegant way to construct
'new' solutions from existing ones, take a permutation $\\sigma
\\in S_5$ permuting the five colours and look on the resulting colored
dodecahedron (which again is a solution) for the (new) face of type A
and project from it to get a new diagram. Probably the correct statement
of the quintominal-dodecahedron-problem is : find all solutions up to
symmetries of the dodecahedron _and_ permutations of the colours.
Likely, the 3 Conway solutions represent the different orbits under this
larger group action. Remains the problem : to which orbit belongs the
top picture??

Leave a Comment