It is perhaps surprising that Alain Connes and Katia Consani, two icons of noncommutative geometry, restrict themselves to define commutative algebraic geometry over $\mathbb{F}_1 $, the field with one element.
My guess of why they stop there is as good as anyone’s. Perhaps they felt that there is already enough noncommutativity in Soule’s gadget-approach (the algebra $\mathcal{A}_X $ as in this post may very well be noncommutative). Perhaps they were only interested in the Bost-Connes system which can be entirely encoded in their commutative $\mathbb{F}_1 $-geometry. Perhaps they felt unsure as to what the noncommutative scheme of an affine noncommutative algebra might be. Perhaps …
Remains the fact that their approach screams for a noncommutative extension. Their basic object is a covariant functor
$N~:~\mathbf{abelian} \rightarrow \mathbf{sets} \qquad A \mapsto N(A) $
from finite abelian groups to sets, together with additional data to the effect that there is a unique minimal integral scheme associated to $N $. In a series of posts on the Connes-Consani paper (starting here) I took some care of getting rid of all scheme-lingo and rephrasing everything entirely into algebras. But then, this set-up can be extended verbatim to noncommuative $\mathbb{F}_1 $-geometry, which should start from a covariant functor
$N~:~\mathbf{groups} \rightarrow \mathbf{sets} $
from all finite groups to sets. Let’s recall quickly what the additional info should be making this functor a noncommutative (affine) F_un scheme :
There should be a finitely generated $\mathbb{C} $-algebra $R $ together with a natural transformation (the ‘evaluation’)
$e~:~N \rightarrow \mathbf{maxi}(R) \qquad N(G) \mapsto Hom_{\mathbb{C}-alg}(R, \mathbb{C} G) $
(both $R $ and the group-algebra $\mathbb{C} G $ may be noncommutative). The pair $(N, \mathbf{maxi}(R)) $ is then called a gadget and there is an obvious notion of ‘morphism’ between gadgets.
The crucial extra ingredient is an affine $\mathbb{Z} $-algebra (possibly noncommutative) $S $
such that $N $ is a subfunctor of $\mathbf{mini}(S)~:~G \mapsto Hom_{\mathbb{Z}-alg}(S,\mathbb{Z} G) $ together with the following universal property :
any affine $\mathbb{Z} $-algebra $T $ having a gadget-morphism $~(N,\mathbf{maxi}(R)) \rightarrow (\mathbf{mini}(T),\mathbf{maxi}(T \otimes_{\mathbb{Z}} \mathbb{C})) $ comes from a $\mathbb{Z} $-algebra morphism $T \rightarrow S $. (If this sounds too cryptic for you, please read the series on C-C mentioned before).
So, there is no problem in defining noncommutative affine F_un-schemes. However, as with any generalization, this only makes sense provided (a) we get something new and (b) we have interesting examples, not covered by the restricted theory.
At first sight we do not get something new as in the only example we did in the C-C-series (the forgetful functor) it is easy to prove (using the same proof as given in this post) that the forgetful-functor $\mathbf{groups} \rightarrow \mathbf{sets} $ still has as its integral form the integral torus $\mathbb{Z}[x,x^{-1}] $. However, both theories quickly diverge beyond this example.
For example, consider the functor
$\mathbf{groups} \rightarrow \mathbf{sets} \qquad G \mapsto G \times G $
Then, if we restrict to abelian finite groups $\mathbf{abelian} $ it is easy to see (again by a similar argument) that the two-dimensional integer torus $\mathbb{Z}[x,y,x^{-1},y^{-1}] $ is the correct integral form. However, this algebra cannot be the correct form for the functor on the category of all finite groups as any $\mathbb{Z} $-algebra map $\phi~:~\mathbb{Z}[x,y,x^{-1},y^{-1}] \rightarrow \mathbb{Z} G $ determines (and is determined by) a pair of commuting units in $\mathbb{Z} G $, so the above functor can not be a subfunctor if we allow non-Abelian groups.
But then, perhaps there isn’t a minimal integral $\mathbb{Z} $-form for this functor? Well, yes there is. Take the free group in two letters (that is, all words in noncommuting $x,y,x^{-1} $ and $y^{-1} $ satisfying only the trivial cancellation laws between a letter and its inverse), then the corresponding integral group-algebra $\mathbb{Z} \mathcal{F}_2 $ does the trick.
Again, the proof-strategy is the same. Given a gadget-morphism we have an algebra map $f~:~T \mapsto \mathbb{C} \mathcal{F}_2 $ and we have to show, using the universal property that the image of $T $ is contained in the integral group-algebra $\mathbb{Z} \mathcal{F}_2 $. Take a generator
$z $ of $T $ then the degree of the image $f(z) $ is bounded say by $d $ and we can always find a subgroup $H \subset \mathcal{F}_2 $ such that $\mathcal{F}_2/H $ is a fnite group and the quotient map $\mathbb{C} \mathcal{F}_2 \rightarrow \mathbb{C} \mathcal{F}_2/H $ is injective on the subspace spanned by all words of degree strictly less than $d+1 $. Then, the usual diagram-chase finishes the proof.
What makes this work is that the free group $\mathcal{F}_2 $ has ‘enough’ subgroups of finite index, a property it shares with many interesting discrete groups. Whence the blurb-message :
if the integers $\mathbb{Z} $ see a discrete group $\Gamma $, then the field $\mathbb{F}_1 $ sees its profinite completion $\hat{\Gamma} = \underset{\leftarrow}{lim}~\Gamma/ H $
 So, yes, we get something new by extending the Connes-Consani approach to the noncommutative world, but do we have interesting examples? As “interesting” is a subjective qualification, we’d better invoke the authority-argument.
So, yes, we get something new by extending the Connes-Consani approach to the noncommutative world, but do we have interesting examples? As “interesting” is a subjective qualification, we’d better invoke the authority-argument.
Alexander Grothendieck (sitting on the right, manifestly not disputing a vacant chair with Jean-Pierre Serre, drinking on the left (a marvelous picture taken by F. Hirzebruch in 1958)) was pushing the idea that profinite completions of arithmetical groups were useful in the study of the absolute Galois group $Gal(\overline{\mathbb{Q}}/\mathbb{Q}) $, via his theory of dessins d’enfants (children;s drawings).
In a previous life, I’ve written a series of posts on dessins d’enfants, so I’ll restrict here to the basics. A smooth projective $\overline{\mathbb{Q}} $-curve $X $ has a Belyi-map $X \rightarrow \mathbb{P}^1_{\overline{\mathbb{Q}}} $ ramified only in three points ${ 0,1,\infty } $. The “drawing” corresponding to $X $ is a bipartite graph, drawn on the Riemann surface $X_{\mathbb{C}} $ obtained by lifting the unit interval $[0,1] $ to $X $. As the absolute Galois group acts on all such curves (and hence on their corresponding drawings), the action of it on these dessins d’enfants may give us a way into the multiple mysteries of the absolute Galois group.
In his “Esquisse d’un programme” (Sketch of a program if you prefer to read it in English) he writes :
“C’est ainsi que mon attention s’est portée vers ce que j’ai appelé depuis la “géométrie algêbrique anabélienne”, dont le point de départ est justement une étude (pour le moment limitée à la caractéristique zéro) de l’action de groupe de Galois “absolus” (notamment les groupes $Gal(\overline{K}/K) $, ou $K $ est une extension de type fini du corps premier) sur des groupes fondamentaux géométriques (profinis) de variétés algébriques (définies sur $K $), et plus particulièrement (rompant avec une tradition bien enracinée) des groupes fondamentaux qui sont trés éloignés des groupes abéliens (et que pour cette raison je nomme “anabéliens”). Parmi ces groupes, et trés proche du groupe $\hat{\pi}_{0,3} $, il y a le compactifié profini du groupe modulaire $SL_2(\mathbb{Z}) $, dont le quotient par le centre $\pm 1 $ contient le précédent comme sous-groupe de congruence mod 2, et peut s’interpréter d’ailleurs comme groupe “cartographique” orienté, savoir celui qui classifie les cartes orientées triangulées (i.e. celles dont les faces des triangles ou des monogones).”
and a bit further, he writes :
“L’élément de structure de $SL_2(\mathbb{Z}) $ qui me fascine avant tout, est bien sur l’action extérieure du groupe de Galois $Gal(\overline{\mathbb{Q}}/\mathbb{Q}) $ sur le compactifié profini. Par le théorème de Bielyi, prenant les compactifiés profinis de sous-groupes d’indice fini de $SL_2(\mathbb{Z}) $, et l’action extérieure induite (quitte à passer également à un sous-groupe overt de $Gal(\overline{\mathbb{Q}},\mathbb{Q}) $), on trouve essentiellement les groupes fondamentaux de toutes les courbes algébriques définis sur des corps de nombres $K $, et l’action extérieure de $Gal(\overline{K}/K) $ dessus.”
So, is there a noncommutative affine variety over $\mathbb{F}_1 $ of which the unique minimal integral model is the integral group algebra of the modular group $\mathbb{Z} \Gamma $ (with $\Gamma = PSL_2(\mathbb{Z}) $? Yes, here it is
$N_{\Gamma}~:~\mathbf{groups} \rightarrow \mathbf{sets} \qquad G \mapsto G_2 \times G_3 $
where $G_n $ is the set of all elements of order $n $ in $G $. The reason behind this is that the modular group is the free group product $C_2 \ast C_3 $.
Fine, you may say, but all this is just algebra. Where is the noncommutative complex variety or the noncommutative integral scheme in all this? Well, we can introduce them too but as this post is already 1300 words long, I’ll better leave this for another time. In case you cannot stop thinking about it, here’s the short answer.
The complex noncommutative variety has as its ‘points’ all finite dimensional simple complex representations of the modular group, and the ‘points’ of the noncommutative $\mathbb{F}_1 $-scheme are exactly the (modular) dessins d’enfants…
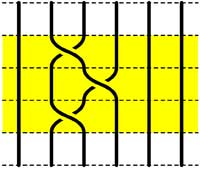
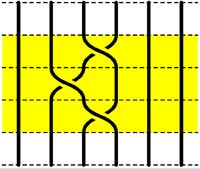
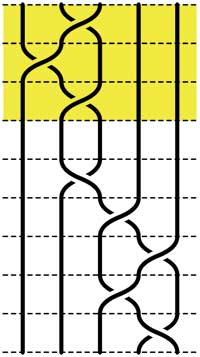
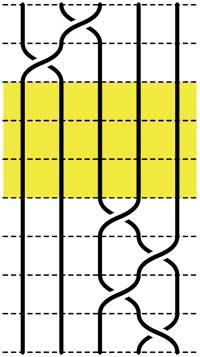
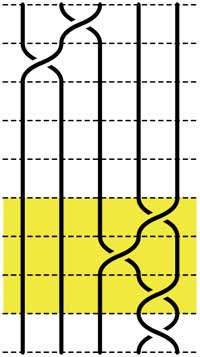
Leave a Comment Recall that an n-braid consists of n strictly descending elastic strings connecting n inputs at the top (named 1,2,…,n) to n outputs at the bottom (labeled 1,2,…,n) upto isotopy (meaning that we may pull and rearrange the strings in any way possible within 3-dimensional space). We can always change the braid slightly such that we can divide the interval between in- and output in a number of subintervals such that in each of those there is at most one crossing.
Recall that an n-braid consists of n strictly descending elastic strings connecting n inputs at the top (named 1,2,…,n) to n outputs at the bottom (labeled 1,2,…,n) upto isotopy (meaning that we may pull and rearrange the strings in any way possible within 3-dimensional space). We can always change the braid slightly such that we can divide the interval between in- and output in a number of subintervals such that in each of those there is at most one crossing. =
= 
 =
=
 =
= =
= =
=