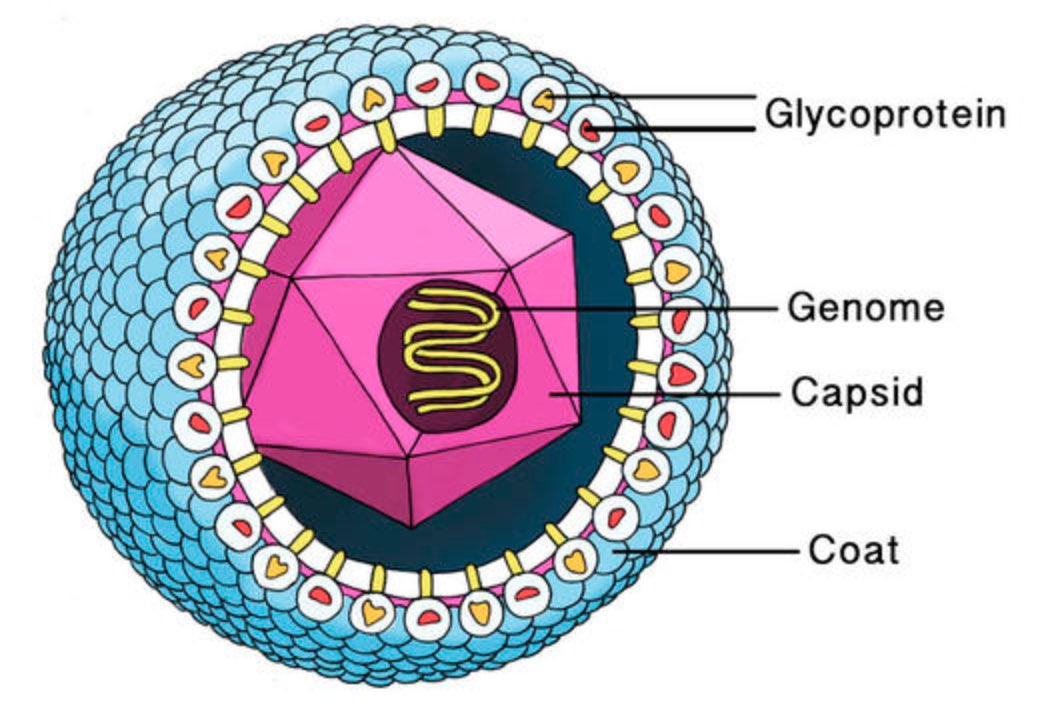
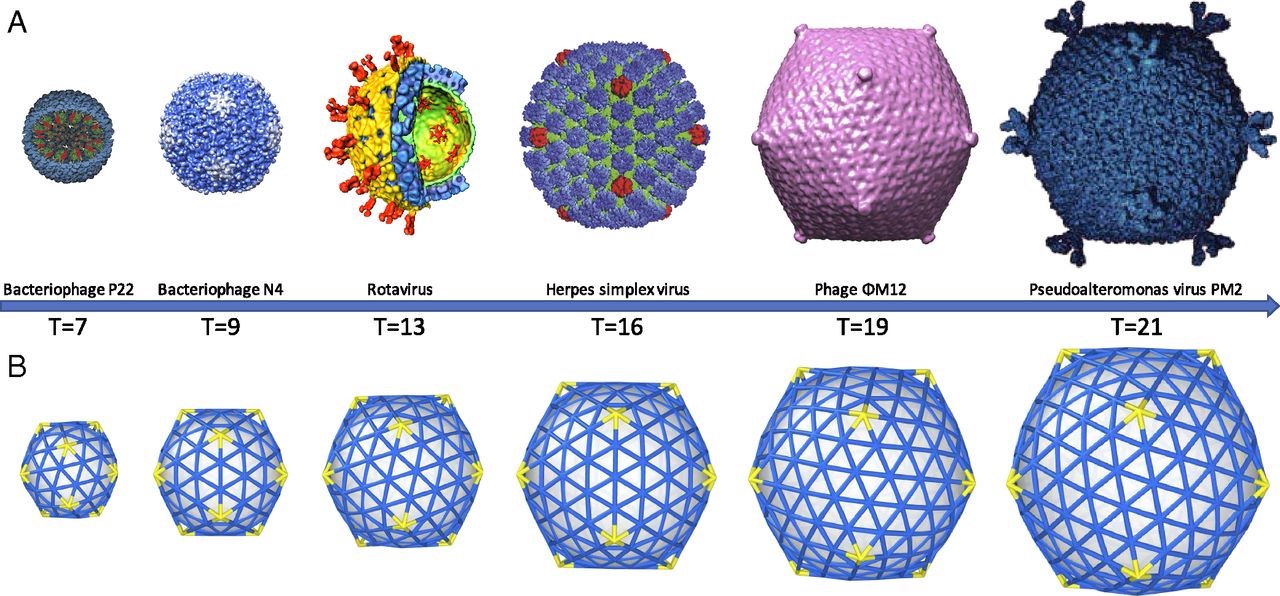
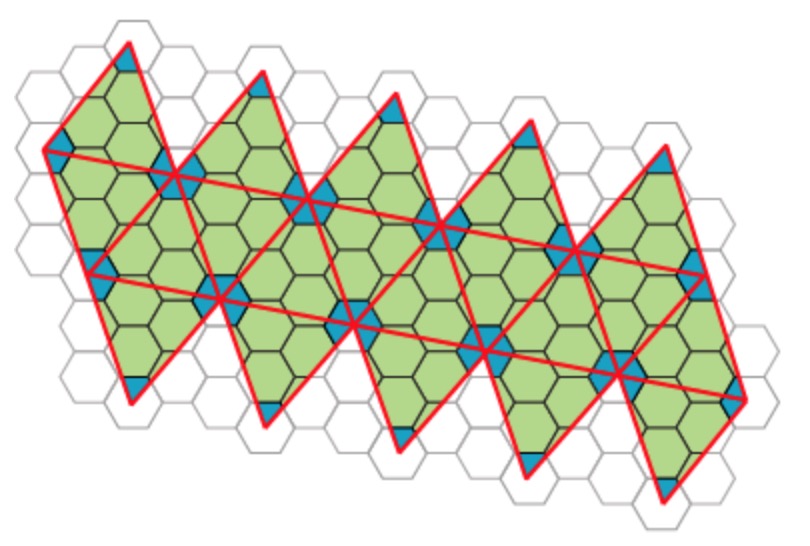
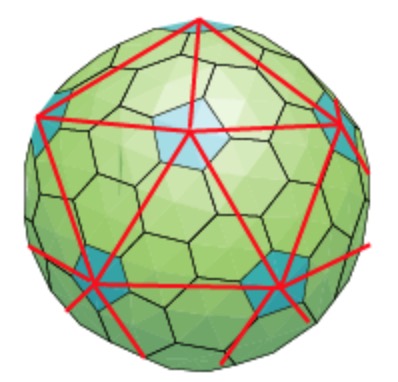
If you look around for mathematical theories of the structure of viruses, you quickly end up with the work of Raidun Twarock and her group at the University of York.
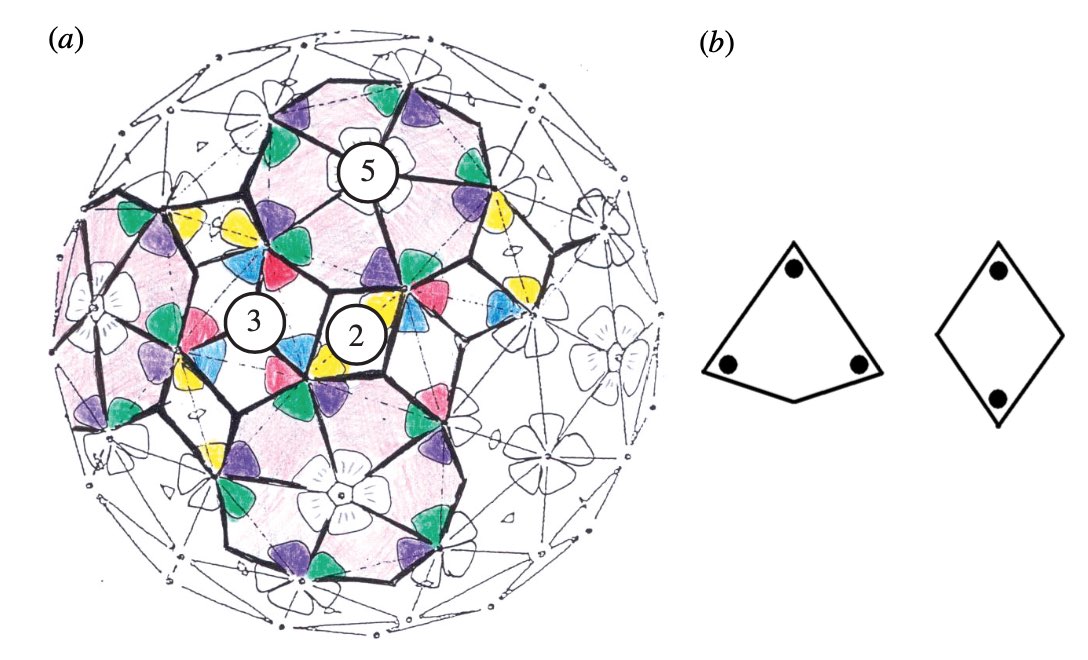
We’ve seen her proposal to extend the Caspar-Klug classification of viruses. Her novel idea to distribute proteins on the viral capsid along Penrose-like tilings shouldn’t be taken too literally. The inherent aperiodic nature of Penrose tiles doesn’t go together well with perfect tilings of the sphere.
Instead, the observation that these capsid tilings resemble somewhat Penrose tilings is a side-effect of another great idea of the York group. Recently, they borrowed techniques from the theory of quasicrystals to gain insight in the inner structure of viruses, in particular on the interaction of the capsid with the genome.
By the crystallographic restriction theorem no $3$-dimensional lattice can have icosahedral symmetry. But, we can construct aperiodic structures (quasicrystals) which have local icosahedral structure, much like Penrose tilings have local $D_5$-symmetry

This is best explained by de Bruijn‘s theory of pentagrids (more on that another time). Here I’ll just mention the representation-theoretic idea.
The isometry group of the standard $5$-dimensional lattice $\mathbb{Z}^5$ is the group of all signed permutation $5 \times 5$ matrices $B_5$ (Young’s hyperoctahedral group). There are two distinct conjugacy classes of subgroups in $B_5$ isomorphic to $D_5$, one such subgroup generated by the permutation matrices
\[
x= \begin{bmatrix}
0 & 1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 1 \\
1 & 0 & 0 & 0 & 0 \end{bmatrix} \qquad \text{and} \qquad
y = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 1 & 0 \\
0 & 0 & 1 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 \end{bmatrix} \]
The traces of $x,x^2$ and $y$, together with the character table of $D_5$ tell us that this $5$-dimensional $D_5$-representation splits as the direct sum of the trivial representation and of the two irreducible $2$-dimensional representations.
\[
\mathbb{R}^5 = A \simeq T \oplus W_1 \oplus W_2 \]
with $T = \mathbb{R} d$, $W_1 = \mathbb{R} u_1 + \mathbb{R} u_2$ and $W_2 = \mathbb{R} w_1 + \mathbb{R} w_2$ where
\[
\begin{cases}
(1,1,1,1,1)=d \\
(1,c_1,c_2,c_3,c_4)= u_1 \\
(0,s_1,s_2,s_3,s_4) = u_2 \\
(1,c_2,c_4,c1,c3)= w_1 \\
(0,s_2,s_4,s_1,s_3)= w_2
\end{cases}
\]
and $c_j=cos(2\pi j/5)$ and $s_j=sin(2 \pi/5)$. We have a $D_5$-projection
\[
\pi : A \rightarrow W_1 \quad (y_0,\dots,y_4) \mapsto \sum_{i=0}^4 y_i(c_i u_1+s_i u_2) \]
The projection maps the vertices of the $5$-dimensional hypercube to a planar configuration with $D_5$-symmetry.
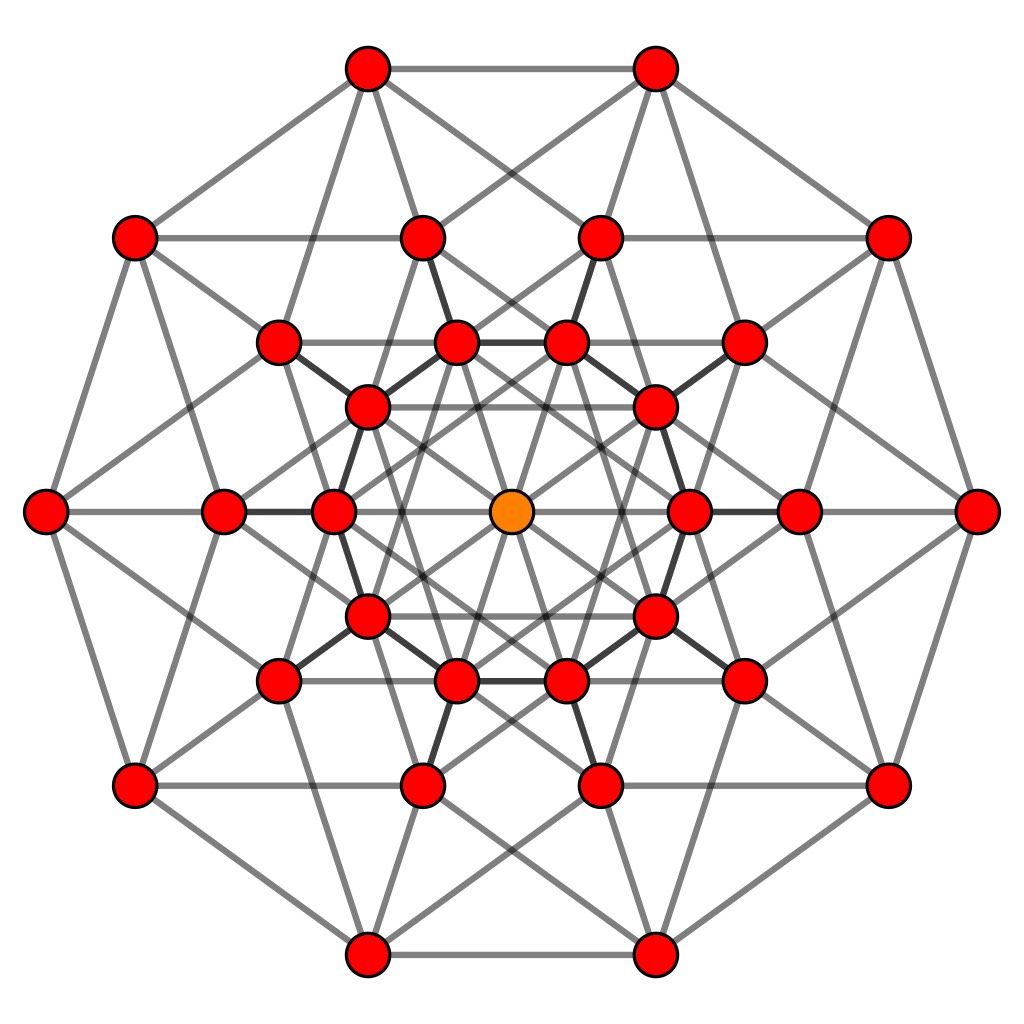
de Bruijn’s results say that if we take suitable ‘windows’ of lattice-points in $\mathbb{Z}^5$ and project them via the $D_5$-equivariant map $\pi$ onto the plane, then the images of these lattice points become the vertices of a rhombic Penrose tiling (and we get all such tilings by choosing our window carefully).

This explains why Penrose tilings have a local $D_5$-symmetry. I’ll try to come back to de Bruijn’s papers in future posts.
But, let’s go back to viruses and the work of Twarock’s group using methods from quasicrystals. Such aperiodic structures with a local icosahedral symmetry can be constructed along similar lines. This time one starts with the standard $6$-dimensional lattice $\mathbb{Z^6}$ with isometry group $B_6$ (signed $6 \times 6$ permutation matrices).
This group has three conjugacy classes of subgroups isomorphic to $A_5$, but for only one of them this $6$-dimensional representation decomposes as the direct sum of the two irreducible $3$-dimensional representations of $A_5$ (the decompositions in the two other cases contain an irreducible of dimension $4$ or $5$ together with trivial factor(s)). A representant of the crystallographic relevant case is given by the signed permutation matrices
\[
x= \begin{bmatrix}
0 & 1 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & -1 & 0 & 0 \\
0 & 0 & -1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & -1 & 0 \\
0 & 0 & 0 & 0 & 0 & -1
\end{bmatrix} \qquad \text{and} \qquad y=
\begin{bmatrix}
0 & 0 & 1 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & -1 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & -1 & 0 & 0
\end{bmatrix} \]
Again, using suitable windows of $\mathbb{Z}^6$-lattice points and using the $A_5$-equivariant projection to one of the two $3$-dimensional components, one obtains quasicrystals with local $A_5$-symmetry.
In this $3$-dimensional case the replacements of the thick and thin rhombi are these four parallellepipeda, known as the Amman blocks
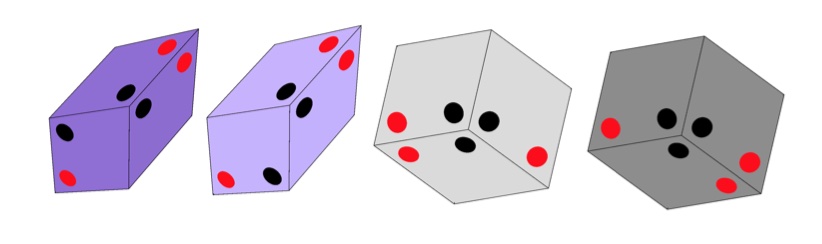
which must be stacked together obeying the gluing condition that dots of the same colour must be adjacent.
Has anyone looked at a possible connection between the four Amman blocks (which come in pairs) and the four (paired) nucleotides in DNA? Just an idle thought…
These blocks grow into quasicrystals with local icosahedral symmetry.
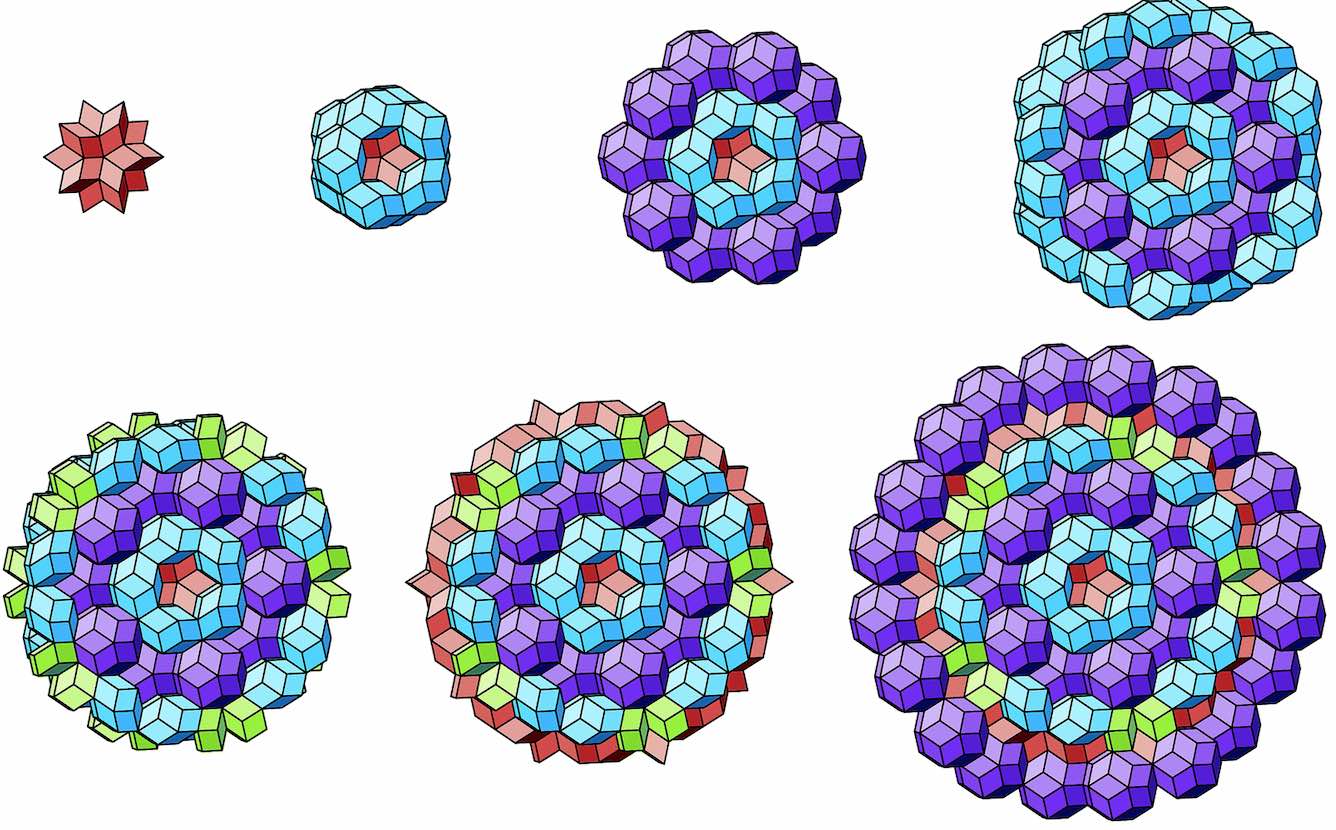
The faces on the boundary of such a sphere-like quasicrystal then look a lot like a Penrose tiling.
How can we connect these group and representation-theoretic ideas to the structure of viruses? Here’s another thought-provoking proposal coming from the York group.
Take the $A_5$ subgroup of the hyperoctahedral group in six dimensiona $B_6$ generated by the above two matrices (giving a good $A_5$-equivariant projection $\pi$ to three dimensional space) and consider an intermediate group
\[
A_5 \subsetneq G \subseteq B_6 \]
Take a point in $\mathbb{R}^6$ and look at its orbit under the isometries of $G$, then all these points have the same distance from the origin in $\mathbb{R}^6$. Now, project this orbit under $\pi$ to get a collection of points in $\mathbb{R}^3$.
As $\pi$ is only $A_5$-equivariant (and not $G$-equivariant) the image points may lie in different shells from the origin. We can try to relate these shells of points to observational data on the inner structures of viruses.
Here’s a pretty convincing instance of such a correlation, taken from the thesis by Emilio Zappa “New group theoretical methods for applications in virology and quasicrystals”.
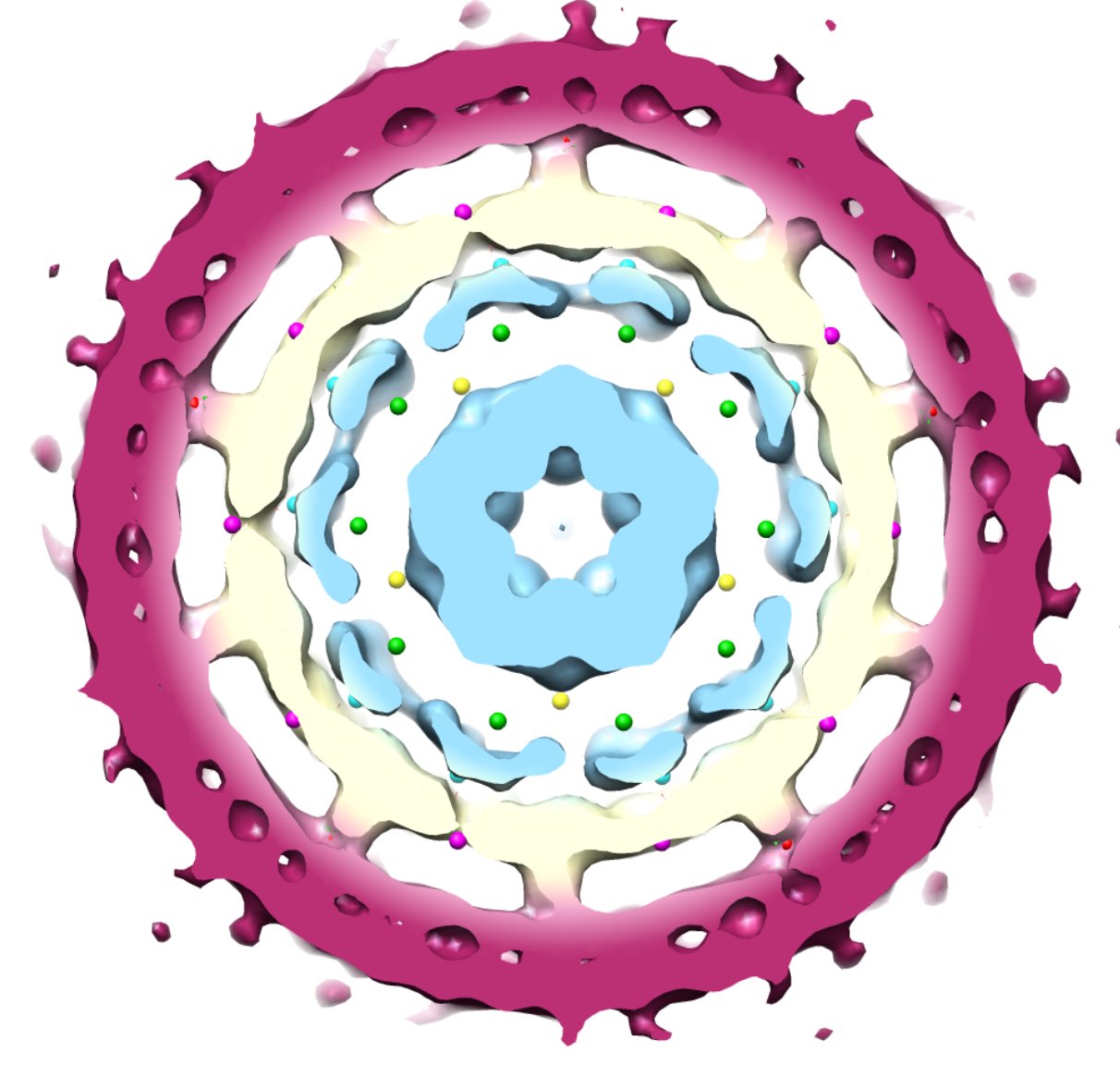
This is the inner structure of the Hepatitis B virus, showing the envelope (purple), capsid protein (cream) and genome (light blue). The coloured dots are the image points in the different shells around the origin.
Do viruses invade us from the sixth dimension??
Comments closed