Tag: noncommutative

what does the monster see?

Published July 16, 2008 by lieven

The Monster is the largest of the 26 sporadic simple groups and has order

808 017 424 794 512 875 886 459 904 961 710 757 005 754 368 000 000 000

= 2^46 3^20 5^9 7^6 11^2 13^3 17 19 23 29 31 41 47 59 71.

It is not so much the size of its order that makes it hard to do actual calculations in the monster, but rather the dimensions of its smallest non-trivial irreducible representations (196 883 for the smallest, 21 296 876 for the next one, and so on).

In characteristic two there is an irreducible representation of one dimension less (196 882) which appears to be of great use to obtain information. For example, Robert Wilson used it to prove that The Monster is a Hurwitz group. This means that the Monster is generated by two elements g and h satisfying the relations

$g^2 = h^3 = (gh)^7 = 1 $

Geometrically, this implies that the Monster is the automorphism group of a Riemann surface of genus g satisfying the Hurwitz bound 84(g-1)=#Monster. That is,

g=9619255057077534236743570297163223297687552000000001=42151199 * 293998543 * 776222682603828537142813968452830193

Or, in analogy with the Klein quartic which can be constructed from 24 heptagons in the tiling of the hyperbolic plane, there is a finite region of the hyperbolic plane, tiled with heptagons, from which we can construct this monster curve by gluing the boundary is a specific way so that we get a Riemann surface with exactly 9619255057077534236743570297163223297687552000000001 holes. This finite part of the hyperbolic tiling (consisting of #Monster/7 heptagons) we’ll call the empire of the monster and we’d love to describe it in more detail.

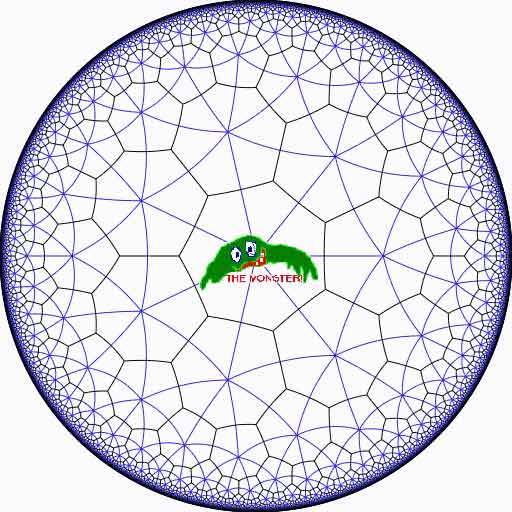
Look at the half-edges of all the heptagons in the empire (the picture above learns that every edge in cut in two by a blue geodesic). They are exactly #Monster such half-edges and they form a dessin d’enfant for the monster-curve.

If we label these half-edges by the elements of the Monster, then multiplication by g in the monster interchanges the two half-edges making up a heptagonal edge in the empire and multiplication by h in the monster takes a half-edge to the one encountered first by going counter-clockwise in the vertex of the heptagonal tiling. Because g and h generated the Monster, the dessin of the empire is just a concrete realization of the monster.

Because g is of order two and h is of order three, the two permutations they determine on the dessin, gives a group epimorphism $C_2 \ast C_3 = PSL_2(\mathbb{Z}) \rightarrow \mathbb{M} $ from the modular group $PSL_2(\mathbb{Z}) $ onto the Monster-group.

In noncommutative geometry, the group-algebra of the modular group $\mathbb{C} PSL_2 $ can be interpreted as the coordinate ring of a noncommutative manifold (because it is formally smooth in the sense of Kontsevich-Rosenberg or Cuntz-Quillen) and the group-algebra of the Monster $\mathbb{C} \mathbb{M} $ itself corresponds in this picture to a finite collection of ‘points’ on the manifold. Using this geometric viewpoint we can now ask the question What does the Monster see of the modular group?

To make sense of this question, let us first consider the commutative equivalent : what does a point P see of a commutative variety X?

Evaluation of polynomial functions in P gives us an algebra epimorphism $\mathbb{C}[X] \rightarrow \mathbb{C} $ from the coordinate ring of the variety $\mathbb{C}[X] $ onto $\mathbb{C} $ and the kernel of this map is the maximal ideal $\mathfrak{m}_P $ of
$\mathbb{C}[X] $ consisting of all functions vanishing in P.

Equivalently, we can view the point $P= \mathbf{spec}~\mathbb{C}[X]/\mathfrak{m}_P $ as the scheme corresponding to the quotient $\mathbb{C}[X]/\mathfrak{m}_P $. Call this the 0-th formal neighborhood of the point P.

This sounds pretty useless, but let us now consider higher-order formal neighborhoods. Call the affine scheme $\mathbf{spec}~\mathbb{C}[X]/\mathfrak{m}_P^{n+1} $ the n-th forml neighborhood of P, then the first neighborhood, that is with coordinate ring $\mathbb{C}[X]/\mathfrak{m}_P^2 $ gives us tangent-information. Alternatively, it gives the best linear approximation of functions near P.
The second neighborhood $\mathbb{C}[X]/\mathfrak{m}_P^3 $ gives us the best quadratic approximation of function near P, etc. etc.

These successive quotients by powers of the maximal ideal $\mathfrak{m}_P $ form a system of algebra epimorphisms

$\ldots \frac{\mathbb{C}[X]}{\mathfrak{m}_P^{n+1}} \rightarrow \frac{\mathbb{C}[X]}{\mathfrak{m}_P^{n}} \rightarrow \ldots \ldots \rightarrow \frac{\mathbb{C}[X]}{\mathfrak{m}_P^{2}} \rightarrow \frac{\mathbb{C}[X]}{\mathfrak{m}_P} = \mathbb{C} $

and its inverse limit $\underset{\leftarrow}{lim}~\frac{\mathbb{C}[X]}{\mathfrak{m}_P^{n}} = \hat{\mathcal{O}}_{X,P} $ is the completion of the local ring in P and contains all the infinitesimal information (to any order) of the variety X in a neighborhood of P. That is, this completion $\hat{\mathcal{O}}_{X,P} $ contains all information that P can see of the variety X.

In case P is a smooth point of X, then X is a manifold in a neighborhood of P and then this completion
$\hat{\mathcal{O}}_{X,P} $ is isomorphic to the algebra of formal power series $\mathbb{C}[[ x_1,x_2,\ldots,x_d ]] $ where the $x_i $ form a local system of coordinates for the manifold X near P.

Right, after this lengthy recollection, back to our question what does the monster see of the modular group? Well, we have an algebra epimorphism

$\pi~:~\mathbb{C} PSL_2(\mathbb{Z}) \rightarrow \mathbb{C} \mathbb{M} $

and in analogy with the commutative case, all information the Monster can gain from the modular group is contained in the $\mathfrak{m} $-adic completion

$\widehat{\mathbb{C} PSL_2(\mathbb{Z})}_{\mathfrak{m}} = \underset{\leftarrow}{lim}~\frac{\mathbb{C} PSL_2(\mathbb{Z})}{\mathfrak{m}^n} $

where $\mathfrak{m} $ is the kernel of the epimorphism $\pi $ sending the two free generators of the modular group $PSL_2(\mathbb{Z}) = C_2 \ast C_3 $ to the permutations g and h determined by the dessin of the pentagonal tiling of the Monster’s empire.

As it is a hopeless task to determine the Monster-empire explicitly, it seems even more hopeless to determine the kernel $\mathfrak{m} $ let alone the completed algebra… But, (surprise) we can compute $\widehat{\mathbb{C} PSL_2(\mathbb{Z})}_{\mathfrak{m}} $ as explicitly as in the commutative case we have $\hat{\mathcal{O}}_{X,P} \simeq \mathbb{C}[[ x_1,x_2,\ldots,x_d ]] $ for a point P on a manifold X.

Here the details : the quotient $\mathfrak{m}/\mathfrak{m}^2 $ has a natural structure of $\mathbb{C} \mathbb{M} $-bimodule. The group-algebra of the monster is a semi-simple algebra, that is, a direct sum of full matrix-algebras of sizes corresponding to the dimensions of the irreducible monster-representations. That is,

$\mathbb{C} \mathbb{M} \simeq \mathbb{C} \oplus M_{196883}(\mathbb{C}) \oplus M_{21296876}(\mathbb{C}) \oplus \ldots \ldots \oplus M_{258823477531055064045234375}(\mathbb{C}) $

with exactly 194 components (the number of irreducible Monster-representations). For any $\mathbb{C} \mathbb{M} $-bimodule $M $ one can form the tensor-algebra

$T_{\mathbb{C} \mathbb{M}}(M) = \mathbb{C} \mathbb{M} \oplus M \oplus (M \otimes_{\mathbb{C} \mathbb{M}} M) \oplus (M \otimes_{\mathbb{C} \mathbb{M}} M \otimes_{\mathbb{C} \mathbb{M}} M) \oplus \ldots \ldots $

and applying the formal neighborhood theorem for formally smooth algebras (such as $\mathbb{C} PSL_2(\mathbb{Z}) $) due to Joachim Cuntz (left) and Daniel Quillen (right) we have an isomorphism of algebras

$\widehat{\mathbb{C} PSL_2(\mathbb{Z})}_{\mathfrak{m}} \simeq \widehat{T_{\mathbb{C} \mathbb{M}}(\mathfrak{m}/\mathfrak{m}^2)} $

where the right-hand side is the completion of the tensor-algebra (at the unique graded maximal ideal) of the $\mathbb{C} \mathbb{M} $-bimodule $\mathfrak{m}/\mathfrak{m}^2 $, so we’d better describe this bimodule explicitly.

Okay, so what’s a bimodule over a semisimple algebra of the form $S=M_{n_1}(\mathbb{C}) \oplus \ldots \oplus M_{n_k}(\mathbb{C}) $? Well, a simple S-bimodule must be either (1) a factor $M_{n_i}(\mathbb{C}) $ with all other factors acting trivially or (2) the full space of rectangular matrices $M_{n_i \times n_j}(\mathbb{C}) $ with the factor $M_{n_i}(\mathbb{C}) $ acting on the left, $M_{n_j}(\mathbb{C}) $ acting on the right and all other factors acting trivially.

That is, any S-bimodule can be represented by a quiver (that is a directed graph) on k vertices (the number of matrix components) with a loop in vertex i corresponding to each simple factor of type (1) and a directed arrow from i to j corresponding to every simple factor of type (2).

That is, for the Monster, the bimodule $\mathfrak{m}/\mathfrak{m}^2 $ is represented by a quiver on 194 vertices and now we only have to determine how many loops and arrows there are at or between vertices.

Using Morita equivalences and standard representation theory of quivers it isn’t exactly rocket science to determine that the number of arrows between the vertices corresponding to the irreducible Monster-representations $S_i $ and $S_j $ is equal to

$dim_{\mathbb{C}}~Ext^1_{\mathbb{C} PSL_2(\mathbb{Z})}(S_i,S_j)-\delta_{ij} $

Now, I’ve been wasting a lot of time already here explaining what representations of the modular group have to do with quivers (see for example here or some other posts in the same series) and for quiver-representations we all know how to compute Ext-dimensions in terms of the Euler-form applied to the dimension vectors.

Right, so for every Monster-irreducible $S_i $ we have to determine the corresponding dimension-vector $~(a_1,a_2;b_1,b_2,b_3) $ for the quiver

$\xymatrix{ & & & &
\vtx{b_1} \\ \vtx{a_1} \ar[rrrru]^(.3){B_{11}} \ar[rrrrd]^(.3){B_{21}}
\ar[rrrrddd]_(.2){B_{31}} & & & & \\ & & & & \vtx{b_2} \\ \vtx{a_2}
\ar[rrrruuu]_(.7){B_{12}} \ar[rrrru]_(.7){B_{22}}
\ar[rrrrd]_(.7){B_{23}} & & & & \\ & & & & \vtx{b_3}} $

Now the dimensions $a_i $ are the dimensions of the +/-1 eigenspaces for the order 2 element g in the representation and the $b_i $ are the dimensions of the eigenspaces for the order 3 element h. So, we have to determine to which conjugacy classes g and h belong, and from Wilson’s paper mentioned above these are classes 2B and 3B in standard Atlas notation.

So, for each of the 194 irreducible Monster-representations we look up the character values at 2B and 3B (see below for the first batch of those) and these together with the dimensions determine the dimension vector $~(a_1,a_2;b_1,b_2,b_3) $.

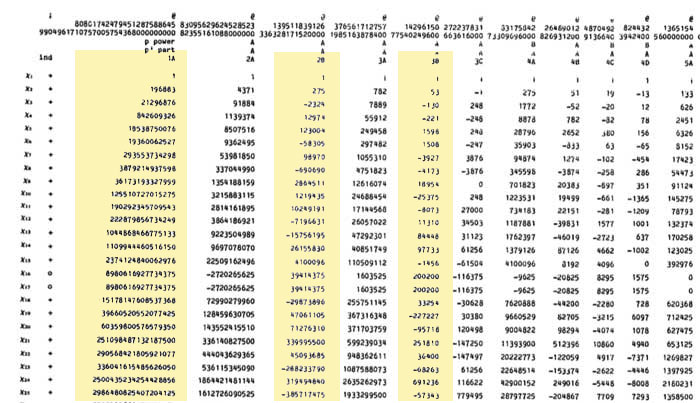
For example take the 196883-dimensional irreducible. Its 2B-character is 275 and the 3B-character is 53. So we are looking for a dimension vector such that $a_1+a_2=196883, a_1-275=a_2 $ and $b_1+b_2+b_3=196883, b_1-53=b_2=b_3 $ giving us for that representation the dimension vector of the quiver above $~(98579,98304,65663,65610,65610) $.

Okay, so for each of the 194 irreducibles $S_i $ we have determined a dimension vector $~(a_1(i),a_2(i);b_1(i),b_2(i),b_3(i)) $, then standard quiver-representation theory asserts that the number of loops in the vertex corresponding to $S_i $ is equal to

$dim(S_i)^2 + 1 – a_1(i)^2-a_2(i)^2-b_1(i)^2-b_2(i)^2-b_3(i)^2 $

and that the number of arrows from vertex $S_i $ to vertex $S_j $ is equal to

$dim(S_i)dim(S_j) – a_1(i)a_1(j)-a_2(i)a_2(j)-b_1(i)b_1(j)-b_2(i)b_2(j)-b_3(i)b_3(j) $

This data then determines completely the $\mathbb{C} \mathbb{M} $-bimodule $\mathfrak{m}/\mathfrak{m}^2 $ and hence the structure of the completion $\widehat{\mathbb{C} PSL_2}_{\mathfrak{m}} $ containing all information the Monster can gain from the modular group.

But then, one doesn’t have to go for the full regular representation of the Monster. Any faithful permutation representation will do, so we might as well go for the one of minimal dimension.

That one is known to correspond to the largest maximal subgroup of the Monster which is known to be a two-fold extension $2.\mathbb{B} $ of the Baby-Monster. The corresponding permutation representation is of dimension 97239461142009186000 and decomposes into Monster-irreducibles

$S_1 \oplus S_2 \oplus S_4 \oplus S_5 \oplus S_9 \oplus S_{14} \oplus S_{21} \oplus S_{34} \oplus S_{35} $

(in standard Atlas-ordering) and hence repeating the arguments above we get a quiver on just 9 vertices! The actual numbers of loops and arrows (I forgot to mention this, but the quivers obtained are actually symmetric) obtained were found after laborious computations mentioned in this post and the details I’ll make avalable here.

Anyone who can spot a relation between the numbers obtained and any other part of mathematics will obtain quantities of genuine (ie. non-Inbev) Belgian beer…

GAMAP 2008

Published July 7, 2008 by lieven

Next week, our annual summer school Geometric and Algebraic Methods with Applications in Physics will start, once again (ive lost count which edition it is).

Because Isar is awol to la douce France, I’ll be responsible (once again) for the web-related stuff of the meeting. So, here a couple of requests to participants/lecturers :

if you are giving a mini-course and would like to have your material online, please contact me and i’ll make you an author of the Arts blog.
if you are a student attending the summerschool and would love to do some Liveblogging about the meeting, please do the same.

I’ll try to do some cross-posting here when it comes to my own lectures (and, perhaps, a few others). For now, I settled on ‘What is noncommutative geometry?’ as a preliminary title, but then, I’m in the position to change the program with a few keystrokes, so I’ll probably change it by then (or remove myself from it altogether…).

At times, I feel it would be more fun to do a few talks on Math-blogging. An entertaining hour could be spend on the forensic investigation of the recent Riemann-Hypothesis-hype in (a good part of) the math-blogosphere…

The F_un folklore

Published June 7, 2008 by lieven

All esoteric subjects have their own secret (sacred) texts. If you opened the Da Vinci Code (or even better, the original The Holy blood and the Holy grail) you will known about a mysterious collection of documents, known as the “Dossiers secrets“, deposited in the Bibliothèque nationale de France on 27 April 1967, which is rumoured to contain the mysteries of the Priory of Sion, a secret society founded in the middle ages and still active today…

The followers of F-un, for $\mathbb{F}_1 $ the field of one element, have their own collection of semi-secret texts, surrounded by whispers, of which they try to decode every single line in search of enlightenment. Fortunately, you do not have to search the shelves of the Bibliotheque National in Paris, but the depths of the internet to find them as huge, bandwidth-unfriendly, scanned documents.

The first are the lecture notes “Lectures on zeta functions and motives” by Yuri I. Manin of a course given in 1991.

One can download a scanned version of the paper from the homepage of Katia Consani as a huge 23.1 Mb file. Of F-un relevance is the first section “Absolute Motives?” in which

“…we describe a highly speculative picture of analogies between arithmetics over $\mathbb{F}_q $ and over $\mathbb{Z} $, cast in the language reminiscent of Grothendieck’s motives. We postulate the existence of a category with tensor product $\times $ whose objects correspond not only to the divisors of the Hasse-Weil zeta functions of schemes over $\mathbb{Z} $, but also to Kurokawa’s tensor divisors. This neatly leads to teh introduction of an “absolute Tate motive” $\mathbb{T} $, whose zeta function is $\frac{s-1}{2\pi} $, and whose zeroth power is “the absolute point” which is teh base for Kurokawa’s direct products. We add some speculations about the role of $\mathbb{T} $ in the “algebraic geometry over a one-element field”, and in clarifying the structure of the gamma factors at infinity.” (loc.cit. p 1-2)

I’d welcome links to material explaining this section to people knowing no motives.

The second one is the unpublished paper “Cohomology determinants and reciprocity laws : number field case” by Mikhail Kapranov and A. Smirnov.

This paper features in blog-posts at the Arcadian Functor, in John Baez’ Weekly Finds and in yesterday’s post at Noncommutative Geometry.

You can download every single page (of 15) as a separate file from here. But, in order to help spreading the Fun-gospel, I’ve made these scans into a single PDF-file which you can download as a 2.6 Mb PDF. In the introduction they say :

“First of all, it is an old idea to interpret combinatorics of finite sets as the $q \rightarrow 1 $ limit of linear algebra over the finite field $\mathbb{F}_q $. This had lead to frequent consideration of the folklore object $\mathbb{F}_1 $, the “field with one element”, whose vector spaces are just sets. One can postulate, of course, that $\mathbf{spec}(\mathbb{F}_1) $ is the absolute point, but the real problem is to develop non-trivial consequences of this point of view.”

They manage to deduce higher reciprocity laws in class field theory within the theory of $\mathbb{F}_1 $ and its field extensions $\mathbb{F}_{1^n} $. But first, let us explain how they define linear algebra over these absolute fields.

Here is a first principle : in doing linear algebra over these fields, there is no additive structure but only scalar multiplication by field elements. So, what are vector spaces over the field with one element? Well, as scalar multiplication with 1 is just the identity map, we have that a vector space is just a set. Linear maps are just set-maps and in particular, a linear isomorphism of a vector space onto itself is a permutation of the set. That is, linear algebra over $\mathbb{F}_1 $ is the same as combinatorics of (finite) sets.

A vector space over $\mathbb{F}_1 $ is just a set; the dimension of such a vector space is the cardinality of the set. The general linear group $GL_n(\mathbb{F}_1) $ is the symmetric group $S_n $, the identification via permutation matrices (having exactly one 1 in every row and column)

Some people prefer to view an $\mathbb{F}_1 $ vector space as a pointed set, the special element being the ‘origin’ $0 $ but as $\mathbb{F}_1 $ doesnt have a zero, there is also no zero-vector. Still, in later applications (such as defining exact sequences and quotient spaces) it is helpful to have an origin. So, let us denote for any set $S $ by $S^{\bullet} = S \cup { 0 } $. Clearly, linear maps between such ‘extended’ spaces must be maps of pointed sets, that is, sending $0 \rightarrow 0 $.

The field with one element $\mathbb{F}_1 $ has a field extension of degree n for any natural number n which we denote by $\mathbb{F}_{1^n} $ and using the above notation we will define this field as :

$\mathbb{F}_{1^n} = \mu_n^{\bullet} $ with $\mu_n $ the group of all n-th roots of unity. Note that if we choose a primitive n-th root $\epsilon_n $, then $\mu_n \simeq C_n $ is the cyclic group of order n.

Now what is a vector space over $\mathbb{F}_{1^n} $? Recall that we only demand units of the field to act by scalar multiplication, so each ‘vector’ $\vec{v} $ determines an n-set of linear dependent vectors $\epsilon_n^i \vec{v} $. In other words, any $\mathbb{F}_{1^n} $-vector space is of the form $V^{\bullet} $ with $V $ a set of which the group $\mu_n $ acts freely. Hence, $V $ has $N=d.n $ elements and there are exactly $d $ orbits for the action of $\mu_n $ by scalar multiplication. We call $d $ the dimension of the vectorspace and a basis consists in choosing one representant for every orbits. That is, $~B = { b_1,\ldots,b_d } $ is a basis if (and only if) $V = { \epsilon_n^j b_i~:~1 \leq i \leq d, 1 \leq j \leq n } $.

So, vectorspaces are free $\mu_n $-sets and hence linear maps $V^{\bullet} \rightarrow W^{\bullet} $ is a $\mu_n $-map $V \rightarrow W $. In particular, a linear isomorphism of $V $, that is an element of $GL_d(\mathbb{F}_{1^n}) $ is a $\mu_n $ bijection sending any basis element $b_i \rightarrow \epsilon_n^{j(i)} b_{\sigma(i)} $ for a permutation $\sigma \in S_d $.

An $\mathbb{F}_{1^n} $-vectorspace $V^{\bullet} $ is a free $\mu_n $-set $V $ of $N=n.d $ elements. The dimension $dim_{\mathbb{F}_{1^n}}(V^{\bullet}) = d $ and the general linear group $GL_d(\mathbb{F}_{1^n}) $ is the wreath product of $S_d $ with $\mu_n^{\times d} $, the identification as matrices with exactly one non-zero entry (being an n-th root of unity) in every row and every column.

This may appear as a rather sterile theory, so let us give an extremely important example, which will lead us to our second principle for developing absolute linear algebra.

Let $q=p^k $ be a prime power and let $\mathbb{F}_q $ be the finite field with $q $ elements. Assume that $q \cong 1~mod(n) $. It is well known that the group of units $\mathbb{F}_q^{\ast} $ is cyclic of order $q-1 $ so by the assumption we can identify $\mu_n $ with a subgroup of $\mathbb{F}_q^{\ast} $.

Then, $\mathbb{F}_q = (\mathbb{F}_q^{\ast})^{\bullet} $ is an $\mathbb{F}_{1^n} $-vectorspace of dimension $d=\frac{q-1}{n} $. In other words, $\mathbb{F}_q $ is an $\mathbb{F}_{1^n} $-algebra. But then, any ordinary $\mathbb{F}_q $-vectorspace of dimension $e $ becomes (via restriction of scalars) an $\mathbb{F}_{1^n} $-vector space of dimension $\frac{e(q-1)}{n} $.

Next time we will introduce more linear algebra definitions (including determinants, exact sequences, direct sums and tensor products) in the realm the absolute fields $\mathbb{F}_{1^n} $ and remarkt that we have to alter the known definitions as we can only use the scalar-multiplication. To guide us, we have the second principle : all traditional results of linear algebra over $\mathbb{F}_q $ must be recovered from the new definitions under the vector-space identification $\mathbb{F}_q = (\mathbb{F}_q^{\ast})^{\bullet} = \mathbb{F}_{1^n} $ when $n=q-1 $. (to be continued)