 We have seen that Conway’s big picture helps us to determine all arithmetic subgroups of $PSL_2(\mathbb{R}) $ commensurable with the modular group $PSL_2(\mathbb{Z}) $, including all groups of monstrous moonshine.
We have seen that Conway’s big picture helps us to determine all arithmetic subgroups of $PSL_2(\mathbb{R}) $ commensurable with the modular group $PSL_2(\mathbb{Z}) $, including all groups of monstrous moonshine.
As there are exactly 171 such moonshine groups, they are determined by a finite subgraph of Conway’s picture and we call the minimal such subgraph the moonshine picture. Clearly, we would like to determine its structure.
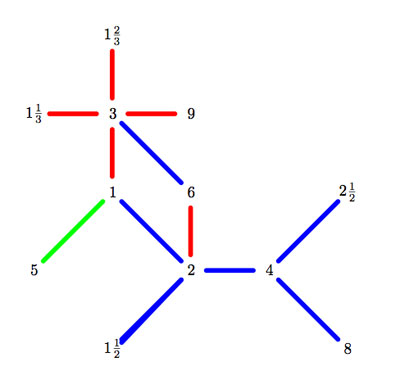
On the left a depiction of a very small part of it. It is the minimal subgraph of Conway’s picture needed to describe the 9 moonshine groups appearing in Duncan’s realization of McKay’s E(8)-observation. Here, only three primes are relevant : 2 (blue lines), 3 (reds) and 5 (green). All lattices are number-like (recall that $M \frac{g}{h} $ stands for the lattice $\langle M e_1 + \frac{g}{h} e_2, e_2 \rangle $).
We observe that a large part of this mini-moonshine picture consists of the three p-tree subgraphs (the blue, red and green tree starting at the 1-lattice $1 = \langle e_1,e_2 \rangle $. Whereas Conway’s big picture is the product over all p-trees with p running over all prime numbers, we observe that the mini-moonshine picture is a very small subgraph of the product of these three subtrees. In fact, there is just one 2-cell (the square 1,2,6,3).
Hence, it seems like a good idea to start our investigation of the full moonshine picture with the determination of the p-subtrees contained in it, and subsequently, worry about higher dimensional cells constructed from them. Surely it will be no major surprise that the prime numbers p that appear in the moonshine picture are exactly the prime divisors of the order of the monster group, that is p=2,3,5,7,11,13,17,19,23,29,31,41,47,59 or 71. Before we can try to determine these 15 p-trees, we need to know more about the 171 moonshine groups.
Recall that the proper way to view the modular subgroup $\Gamma_0(N) $ is as the subgroup fixing the two lattices $L_1 $ and $L_N $, whence we will write $\Gamma_0(N)=\Gamma_0(N|1) $, and, by extension we will denote with $\Gamma_0(X|Y) $ the subgroup fixing the two lattices $L_X $ and $L_Y $.
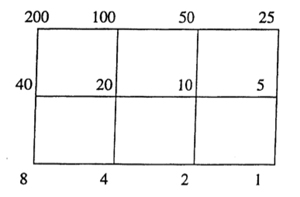 As $\Gamma_0(N) $ fixes $L_1 $ and $L_N $ it also fixes all lattices in the (N|1)-thread, that is all lattices occurring in a shortest path from $L_1 $ to $L_N $ (on the left a picture of the (200|1)-thread).
As $\Gamma_0(N) $ fixes $L_1 $ and $L_N $ it also fixes all lattices in the (N|1)-thread, that is all lattices occurring in a shortest path from $L_1 $ to $L_N $ (on the left a picture of the (200|1)-thread).
If $N=p_1^{a_1} p_2^{a_2} \ldots p_k^{a_k} $, then the (N|1)-thread has $2^k $ involutions as symmetries, called the Atkin-Lehner involutions. For every exact divisor $e || N $ (that is, $e|N $ and $gcd(e,\frac{N}{e})=1 $ we have an involution $W_e $ which acts by sending each point in the thread-cell corresponding to the prime divisors of $e $ to its antipodal cell-point and acts as the identity on the other prime-axes. For example, in the (200|1)-thread on the left, $W_8 $ is the left-right reflexion, $W_{25} $ the top-bottom reflexion and $W_{200} $ the antipodal reflexion. The set of all exact divisors of N becomes the group $~(\mathbb{Z}/2\mathbb{Z})^k $ under the operation $e \ast f = \frac{e \times f}{gcd(e,f)^2} $.
 Most of the moonshine groups are of the form $\Gamma_0(n|h)+e,f,g,… $ for some $N=h.n $ such that $h | 24 $ and $h^2 | N $. The group $\Gamma_0(n|h) $ is then conjugate to the modular subgroup $\Gamma_0(\frac{n}{h}) $ by the element $\begin{bmatrix} h & 0 \ 0 & 1 \end{bmatrix} $. With $\Gamma_0(n|h)+e,f,g,… $ we mean that the group $\Gamma_0(n|h) $ is extended with the involutions $W_e,W_f,W_g,… $. If we simply add all Atkin-Lehner involutions we write $\Gamma_0(n|h)+ $ for the resulting group.
Most of the moonshine groups are of the form $\Gamma_0(n|h)+e,f,g,… $ for some $N=h.n $ such that $h | 24 $ and $h^2 | N $. The group $\Gamma_0(n|h) $ is then conjugate to the modular subgroup $\Gamma_0(\frac{n}{h}) $ by the element $\begin{bmatrix} h & 0 \ 0 & 1 \end{bmatrix} $. With $\Gamma_0(n|h)+e,f,g,… $ we mean that the group $\Gamma_0(n|h) $ is extended with the involutions $W_e,W_f,W_g,… $. If we simply add all Atkin-Lehner involutions we write $\Gamma_0(n|h)+ $ for the resulting group.
Finally, whenever $h \not= 1 $ there is a subgroup $\Gamma_0(n||h)+e,f,g,… $ which is the kernel of a character $\lambda $ being trivial on $\Gamma_0(N) $ and on all involutions $W_e $ for which every prime dividing $e $ also divides $\frac{n}{h} $, evaluating to $e^{\frac{2\pi i}{h}} $ on all cosets containing $\begin{bmatrix} 1 & \frac{1}{h} \ 0 & 1 \end{bmatrix} $ and to $e^{\pm \frac{2 \pi i }{h}} $ for cosets containing $\begin{bmatrix} 1 & 0 \ n & 0 \end{bmatrix} $ (with a + sign if $\begin{bmatrix} 0 & -1 \ N & 0 \end{bmatrix} $ is present and a – sign otherwise). Btw. it is not evident at all that this is a character, but hard work shows it is!
Clearly there are heavy restrictions on the numbers that actually occur in moonshine. In the paper On the discrete groups of moonshine, John Conway, John McKay and Abdellah Sebbar characterized the 171 arithmetic subgroups of $PSL_2(\mathbb{R}) $ occuring in monstrous moonshine as those of the form $G = \Gamma_0(n || h)+e,f,g,… $ which are
- (a) of genus zero, meaning that the quotient of the upper-half plane by the action of $G \subset PSL_2(\mathbb{R}) $ by Moebius-transformations gives a Riemann surface of genus zero,
- (b) the quotient group $G/\Gamma_0(nh) $ is a group of exponent 2 (generated by some Atkin-Lehner involutions), and
- (c) every cusp can be mapped to $\infty $ by an element of $PSL_2(\mathbb{R}) $ which conjugates the group to one containing $\Gamma_0(nh) $.
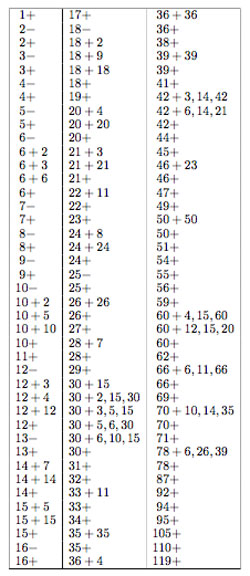
Now, if $\Gamma_0(n || h)+e,f,g,… $ is of genus zero, so is the larger group $\Gamma_0(n | h)+e,f,g,… $, which in turn, is conjugated to the group $\Gamma_0(\frac{n}{h})+e,f,g,… $. Therefore, we need a list of all groups of the form $\Gamma_0(\frac{n}{h})+e,f,g,… $ which are of genus zero. There are exactly 123 of them, listed on the right.
How does this help to determine the structure of the p-subtree of the moonshine picture for the fifteen monster-primes p? Look for the largest p-power $p^k $ such that $p^k+e,f,g… $ appears in the list. That is for p=2,3,5,7,11,13,17,19,23,29,31,41,47,59,71 these powers are resp. 5,3,2,2,1,1,1,1,1,1,1,1,1,1,1. Next, look for the largest p-power $p^l $ dividing 24 (that is, 3 for p=2, 1 for p=3 and 0 for all other primes). Then, these relevant moonshine groups contain the modular subgroup $\Gamma_0(p^{k+2l}) $ and are contained in its normalizer in $PSL_2(\mathbb{R}) $ which by the Atkin-Lehner theorem is precisely the group $\Gamma_0(p^{k+l}|p^l)+ $.
Right, now the lattices fixed by $\Gamma_0(p^{k+2l}) $ (and permuted by its normalizer), that is the lattices in our p-subtree, are those that form the $~(p^{k+2l}|1) $-snake in Conway-speak. That is, the lattices whose hyper-distance to the $~(p^{k+l}|p^l) $-thread divides 24. So for all primes larger than 2 or 3, the p-tree is just the $~(p^l|1) $-thread.
For p=3 the 3-tree is the (243|1)-snake having the (81|3)-thread as its spine. It contains the following lattices, all of which are number-like.
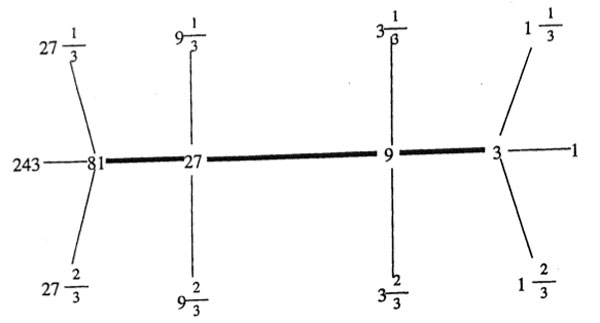
Depicting the 2-tree, which is the (2048|1)-snake may take a bit longer… Perhaps someone should spend some time figuring out which cells of the product of these fifteen trees make up the moonshine picture!
 Bloomsday has a tradition of bringing drastic changes to this blog.
Bloomsday has a tradition of bringing drastic changes to this blog. Time to wrap up this series on
Time to wrap up this series on  They can be described using the mini-moonshine picture on the right. They are :
They can be described using the mini-moonshine picture on the right. They are :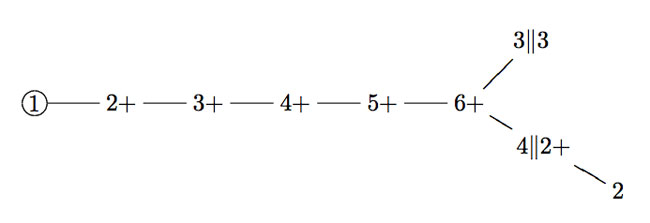
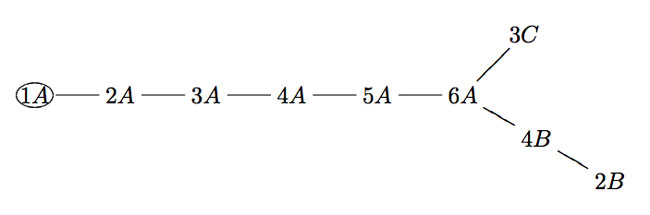
 As $\Gamma_0(N) $ fixes $L_1 $ and $L_N $ it also fixes all lattices in the (N|1)-thread, that is all lattices occurring in a shortest path from $L_1 $ to $L_N $ (on the left a picture of the (200|1)-thread).
As $\Gamma_0(N) $ fixes $L_1 $ and $L_N $ it also fixes all lattices in the (N|1)-thread, that is all lattices occurring in a shortest path from $L_1 $ to $L_N $ (on the left a picture of the (200|1)-thread). Most of the moonshine groups are of the form $\Gamma_0(n|h)+e,f,g,… $ for some $N=h.n $ such that $h | 24 $ and $h^2 | N $. The group $\Gamma_0(n|h) $ is then conjugate to the modular subgroup $\Gamma_0(\frac{n}{h}) $ by the element $\begin{bmatrix} h & 0 \ 0 & 1 \end{bmatrix} $. With $\Gamma_0(n|h)+e,f,g,… $ we mean that the group $\Gamma_0(n|h) $ is extended with the involutions $W_e,W_f,W_g,… $. If we simply add all Atkin-Lehner involutions we write $\Gamma_0(n|h)+ $ for the resulting group.
Most of the moonshine groups are of the form $\Gamma_0(n|h)+e,f,g,… $ for some $N=h.n $ such that $h | 24 $ and $h^2 | N $. The group $\Gamma_0(n|h) $ is then conjugate to the modular subgroup $\Gamma_0(\frac{n}{h}) $ by the element $\begin{bmatrix} h & 0 \ 0 & 1 \end{bmatrix} $. With $\Gamma_0(n|h)+e,f,g,… $ we mean that the group $\Gamma_0(n|h) $ is extended with the involutions $W_e,W_f,W_g,… $. If we simply add all Atkin-Lehner involutions we write $\Gamma_0(n|h)+ $ for the resulting group.