Last time we saw
that a curve defined over $\overline{\mathbb{Q}} $ gives rise
to a permutation representation of $PSL_2(\mathbb{Z}) $ or one
of its subgroups $\Gamma_0(2) $ (of index 2) or
$\Gamma(2) $ (of index 6). As the corresponding
monodromy group is finite, this representation factors through a normal
subgroup of finite index, so it makes sense to look at the profinite
completion of $SL_2(\mathbb{Z}) $, which is the inverse limit
of finite
groups $\underset{\leftarrow}{lim}~SL_2(\mathbb{Z})/N $
where N ranges over all normalsubgroups of finite index. These
profinte completions are horrible beasts even for easy groups such as
$\mathbb{Z} $. Its profinite completion
is
$\underset{\leftarrow}{lim}~\mathbb{Z}/n\mathbb{Z} =
\prod_p \hat{\mathbb{Z}}_p $
where the right hand side
product of p-adic integers ranges over all prime numbers! The
_absolute Galois group_
$G=Gal(\overline{\mathbb{Q}}/\mathbb{Q}) $ acts on all curves
defined over $\overline{\mathbb{Q}} $ and hence (via the Belyi
maps ans the corresponding monodromy permutation representation) there
is an action of $G $ on the profinite completions of the
carthographic groups.
This is what Grothendieck calls anabelian
algebraic geometry
Returning to the general
case, since finite maps can be interpreted as coverings over
$\overline{\mathbb{Q}} $ of an algebraic curve defined over
the prime field $~\mathbb{Q} $ itself, it follows that the
Galois group $G $ of $\overline{\mathbb{Q}} $ over
$~\mathbb{Q} $ acts on the category of these maps in a
natural way.
For instance, the operation of an automorphism
$~\gamma \in G $ on a spherical map given by the rational
function above is obtained by applying $~\gamma $ to the
coefficients of the polynomials P , Q. Here, then, is that
mysterious group $G $ intervening as a transforming agent on
topologico- combinatorial forms of the most elementary possible
nature, leading us to ask questions like: are such and such oriented
maps ‚conjugate or: exactly which are the conjugates of a given
oriented map? (Visibly, there is only a finite number of these).
I considered some concrete cases (for coverings of low degree) by
various methods, J. Malgoire considered some others ‚ I doubt that
there is a uniform method for solving the problem by computer. My
reflection quickly took a more conceptual path, attempting to
apprehend the nature of this action of G.
One sees immediately
that roughly speaking, this action is expressed by a certain
outer action of G on the profinite com- pactification of the
oriented cartographic group $C_+^2 = \Gamma_0(2) $ , and this
action in its turn is deduced by passage to the quotient of the
canonical outer action of G on the profinite fundamental group
$\hat{\pi}_{0,3} $ of
$(U_{0,3})_{\overline{\mathbb{Q}}} $ where
$U_{0,3} $ denotes the typical curve of genus 0 over the
prime field Q, with three points re- moved.
This is how my
attention was drawn to what I have since termed anabelian
algebraic geometry, whose starting point was exactly a study
(limited for the moment to characteristic zero) of the action of
absolute Galois groups (particularly the groups Gal(K/K),
where K is an extension of finite type of the prime field) on
(profinite) geometric fundamental groups of algebraic varieties
(defined over K), and more particularly (break- ing with a
well-established tradition) fundamental groups which are very far
from abelian groups (and which for this reason I call
anabelian).
Among these groups, and very close to
the group $\hat{\pi}_{0,3} $ , there is the profinite
compactification of the modular group $Sl_2(\mathbb{Z}) $,
whose quotient by its centre ±1 contains the former as congruence
subgroup mod 2, and can also be interpreted as an oriented
cartographic group, namely the one classifying triangulated
oriented maps (i.e. those whose faces are all triangles or
monogons).
and a bit further, on page
250
I would like to conclude this rapid outline
with a few words of commentary on the truly unimaginable richness
of a typical anabelian group such as $SL_2(\mathbb{Z}) $
doubtless the most remarkable discrete infinite group ever
encountered, which appears in a multiplicity of avatars (of which
certain have been briefly touched on in the present report), and which
from the point of view of Galois-Teichmuller theory can be
considered as the fundamental ‚building block‚ of the
Teichmuller tower
The element of the structure of
$Sl_2(\mathbb{Z}) $ which fascinates me above all is of course
the outer action of G on its profinite compactification. By
Bielyi’s theorem, taking the profinite compactifications of subgroups
of finite index of $Sl_2(\mathbb{Z}) $, and the induced
outer action (up to also passing to an open subgroup of G), we
essentially find the fundamental groups of all algebraic curves (not
necessarily compact) defined over number fields K, and the outer
action of $Gal(\overline{K}/K) $ on them at least it is
true that every such fundamental group appears as a quotient of one
of the first groups.
Taking the anabelian yoga
(which remains conjectural) into account, which says that an anabelian
algebraic curve over a number field K (finite extension of Q) is
known up to isomorphism when we know its mixed fundamental group (or
what comes to the same thing, the outer action of
$Gal(\overline{K}/K) $ on its profinite geometric
fundamental group), we can thus say that
all algebraic
curves defined over number fields are contained in the profinite
compactification $\widehat{SL_2(\mathbb{Z})} $ and in the
knowledge of a certain subgroup G of its group of outer
automorphisms!
To study the absolute
Galois group $Gal(\overline{\mathbb{\mathbb{Q}}}/\mathbb{Q}) $ one
investigates its action on dessins denfants. Each dessin will be part of
a finite family of dessins which form one orbit under the Galois action
and one needs to find invarians to see whether two dessins might belong
to the same orbit. Such invariants are called _Galois invariants_ and
quite a few of them are known.
Among these the easiest to compute
are
- the valency list of a dessin : that is the valencies of all
vertices of the same type in a dessin - the monodromy group of a dessin : the subgroup of the symmetric group $S_d $ where d is
the number of edges in the dessin generated by the partitions $\tau_0 $
and $\tau_1 $ For example, we have seen
before that the two
Mathieu-dessins
form a Galois orbit. As graphs (remeber we have to devide each
of the edges into two and the midpoints of these halfedges form one type
of vertex, the other type are the black vertices in the graphs) these
are isomorphic, but NOT as dessins as we have to take the embedding of
them on the curve into account. However, for both dessins the valency
lists are (white) : (2,2,2,2,2,2) and (black) :
(3,3,3,1,1,1) and one verifies that both monodromy groups are
isomorphic to the Mathieu simple group $M_{12} $ though they are
not conjugated as subgroups of $S_{12} $.
Recently, new
Galois invariants were obtained from physics. In Children’s drawings
from Seiberg-Witten curves
the authors argue that there is a close connection between Grothendiecks
programme of classifying dessins into Galois orbits and the physics
problem of classifying phases of N=1 gauge theories…
Apart
from curves defined over $\overline{\mathbb{Q}} $ there are
other sources of semi-simple $SL_2(\mathbb{Z}) $
representations. We will just mention two of them and may return to them
in more detail later in the course.
Sporadic simple groups and
their representations There are 26 exceptional finite simple groups
and as all of them are generated by two elements, there are epimorphisms
$\Gamma(2) \rightarrow S $ and hence all their representations
are also semi-simple $\Gamma(2) $-representations. In fact,
looking at the list of ‘standard generators’ of the sporadic
simples
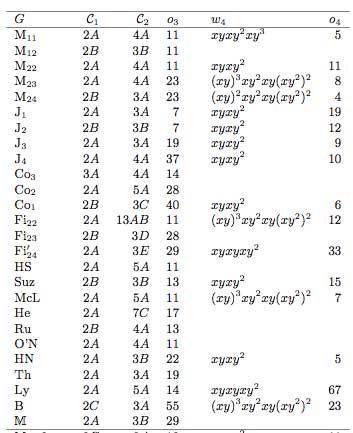
(here the conjugacy classes of the generators follow the
notation of the Atlas project) we see that all but
possibly one are epimorphic images of $\Gamma_0(2) = C_2 \ast
C_{\infty} $ and that at least 12 of then are epimorphic images
of $PSL_2(\mathbb{Z}) = C_2 \ast
C_3 $.
Rational conformal field theories Another
source of $SL_2(\mathbb{Z}) $ representations is given by the
modular data associated to rational conformal field theories.
 These
These
representations also factor through a quotient by a finite index normal
subgroup and are therefore again semi-simple
$SL_2(\mathbb{Z}) $-representations. For a readable
introduction to all of this see chapter 6 \”Modular group
representations throughout the realm\” of the
book Moonshine beyond the monster the bridge connecting algebra, modular forms and physics by Terry
Gannon. In fact, the whole book
is a good read. It introduces a completely new type of scientific text,
that of a neverending survey paper…
 Just as cartographers like
Just as cartographers like