Tag: modular

Hexagonal Moonshine (3)

Published July 13, 2007 by lieven

Hexagons keep on popping up in the representation theory of the modular group and its close associates. We have seen before that singularities in 2-dimensional representation varieties of the three string braid group $B_3 $ are ‘clanned together’ in hexagons and last time Ive mentioned (in passing) that the representation theory of the modular group is controlled by the double quiver of the extended Dynkin diagram $\tilde{A_5} $, which is an hexagon…

Today we’re off to find representations of the extended modular group $\tilde{\Gamma} = PGL_2(\mathbb{Z}) $, which is obtained by adding to the modular group (see this post for a proof of generation)

$\Gamma = \langle U=\begin{bmatrix} 0 & -1 \\\ 1 & 0 \end{bmatrix},V=\begin{bmatrix} 0 & 1 \\\ -1 & 1 \end{bmatrix} \rangle $ the matrix $R=\begin{bmatrix} 0 & 1 \\\ 1 & 0 \end{bmatrix} $

In terms of generators and relations, one easily verfifies that

$\tilde{\Gamma} = \langle~U,V,R~|~U^2=R^2=V^3=(RU)^2=(RV)^2=1~\rangle $

and therefore $\tilde{\Gamma} $ is the amalgamated free product of the dihedral groups $D_2 $ and $D_3 $ over their common subgroup $C_2 = \langle~R~\rangle $, that is

$\tilde{\Gamma} = \langle U,R | U^2=R^2=(RU)^2=1 \rangle \ast_{\langle R | R^2=1 \rangle} \langle V,R | V^3=R^2=(RV)^2=1 \rangle = D_2 \ast_{C_2} D_3 $

From this description it is easy to find all n-dimensional $\tilde{\Gamma} $-representations $V $ and relate them to quiver-representations. $D_2 = C_2 \times C_2 $ and hence has 4 1-dimensonal simples $S_1,S_2,S_3,S_4 $. Restricting $V\downarrow_{D_2} $ to the subgroup $D_2 $ it decomposes as

$V \downarrow_{D_2} \simeq S_1^{\oplus a_1} \oplus S_2^{\oplus a_2} \oplus S_3^{\oplus a_3} \oplus S_4^{\oplus a_4} $ with $a_1+a_2+a_3+a_4=n $

Similarly, because $D_3=S_3 $ has two one-dimensional representations $T,S $ (the trivial and the sign representation) and one simple 2-dimensional representation $W $, restricting $V $ to this subgroup gives a decomposition

$V \downarrow_{D_3} \simeq T^{b_1} \oplus S^{\oplus b_2} \oplus W^{\oplus b_3} $, this time with $b_1+b_2+2b_3=n $

Restricting both decompositions further down to the common subgroup $C_2 $ one obtains a $C_2 $-isomorphism $V \downarrow_{D_2} \rightarrow^{\phi} V \downarrow_{D_3} $ which implies also that the above numbers must be chosen such that $a_1+a_3=b_1+b_3 $ and $a_2+a_4=b_2+b_3 $. We can summarize all this info about $V $ in a representation of the quiver

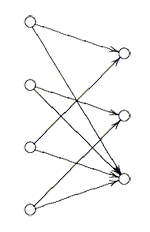Here, the vertex spaces on the left are the iso-typical factors of $V \downarrow_{D_2} $ and those on the right those of $V \downarrow_{D_3} $ and the arrows give the block-components of the $C_2 $-isomorphism $\phi $. The nice things is that one can also reverse this process to get all $\tilde{\Gamma} $-representations from $\theta $-semistable representations of this quiver (having the additional condition that the square matrix made of the arrows is invertible) and isomorphisms of group-representation correspond to those of quiver-representations!

This proves that for all n the varieties of n-dimensional representations $\mathbf{rep}_n~\tilde{\Gamma} $ are smooth (but have several components corresponding to the different dimension vectors $~(a_1,a_2,a_3,a_4;b_1,b_2,b_3) $ such that $\sum a_i = n = b_1+b_2+2b_3 $.

The basic principle of _M-geometry_ is that a lot of the representation theory follows from the ‘clan’ (see this post) determined by the simples of smallest dimensions. In the case of the extended modular group $\tilde{\Gamma} $ it follows that there are exactly 4 one-dimensional simples and exactly 4 2-dimensional simples, corresponding to the dimension vectors

$\begin{cases} a=(0,0,0,1;0,1,0) \\\ b=(0,1,0,0;0,1,0) \\\ c=(1,0,0,0;1,0,0) \\\ d=(0,0,1,0;1,0,0) \end{cases} $ resp. $\begin{cases} e=(0,1,1,0;0,0,1) \\\ f=(1,0,0,1;0,0,1) \\\ g=(0,0,1,1;0,0,1) \\\ h=(1,1,0,0;0,0,1) \end{cases} $

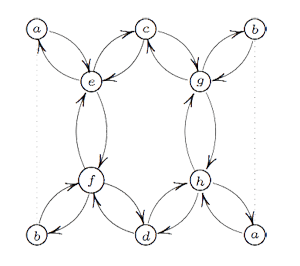If one calculates the ‘clan’ of these 8 simples one obtains the double quiver of the graph on the left. Note that a and b appear twice, so one should glue the left and right hand sides together as a Moebius-strip. That is, the clan determining the representation theory of the extended modular group is a Moebius strip made of two hexagons!

However, one should not focuss too much on the hexagons (that is, the extended Dynkin diagram $\tilde{A_5} $) here. The two ‘backbones’ (e–f and g–h) have their vertices corresponding to 2-dimensional simples whereas the topand bottom vertices correspond to one-dimensional simples. Hence, the correct way to look at this clan is as two copies of the double quiver of the extended Dynkin diagram $\tilde{D_5} $ glued over their leaf vertices to form a Moebius strip. Remark that the components of the sotropic root of $\tilde{D_5} $ give the dimensions of the corresponding $\tilde{\Gamma} $ simples.

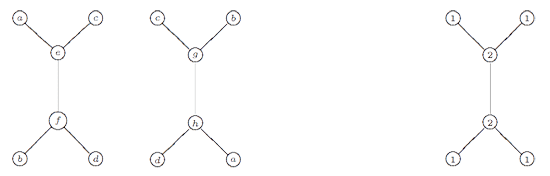
The remarkable ubiquity of (extended) Dynkins never ceases to amaze!

Generators of modular subgroups

Published July 12, 2007 by lieven

In older NeverEndingBooks-posts (and here) proofs were given that the modular group $\Gamma = PSL_2(\mathbb{Z}) $ is the group free product $C_2 \ast C_3 $, so let’s just skim over details here. First one observes that $\Gamma $ is generated by (the images of) the invertible 2×2 matrices

$U= \begin{bmatrix} 0 & -1 \\\ 1 & 0 \end{bmatrix} $ and $V= \begin{bmatrix} 0 & 1 \\\ -1 & 1 \end{bmatrix} $

A way to see this is to consider X=U.V and Y=V.U and notice that multiplying with powers of X adds multiples of the second row to the first (multiply on the left) or multiples of the first column to the second (multiply on the right) and the other cases are handled by taking multiples with powers of Y. Use this together with the fact that matrices in $GL_2(\mathbb{Z}) $ have their rows and columns made of coprime numbers to get any such matrix by multiplication on the left or right by powers of X and Y into the form

$\begin{bmatrix} \pm 1 & 0 \\\ 0 & \pm 1 \end{bmatrix} $ and because $U^2=V^3=\begin{bmatrix} -1 & 0 \\\ 0 & -1 \end{bmatrix} $

we see that $\Gamma $ is an epimorphic image of $C_2 \ast C_3 $. To prove isomorphism one can use the elegant argument due to Roger Alperin considering the action of the Moebius transformations $u(z) = -\frac{1}{z} $ and $v(z) = \frac{1}{1-z} $ (with $v^{-1}(z) = 1-\frac{1}{z} $) induced by the generators U and V on the sets $\mathcal{P} $ and $\mathcal{N} $ of all positive (resp. negative) irrational real numbers. Observe that

$u(\mathcal{P}) \subset \mathcal{N} $ and $v^{\pm}(\mathcal{N}) \subset \mathcal{P} $

Hence, if $w $ is a word in $u $ and $v^{\pm} $ of off length we either have $w(\mathcal{P}) \subset \mathcal{N} $ or $w(\mathcal{N}) \subset \mathcal{P} $ so $w $ can never be the identity. If the length is even we can conjugate $w $ such that it starts with $v^{\pm} $. If it starts with $v $ then $w(\mathcal{P}) \subset v(\mathcal{N}) $ is a subset of positive rationals less than 1 whereas if it starts with $v^{-1} $ then $w(\mathcal{P}) \subset v^{-1}(\mathcal{N}) $ is a subset of positive rationals greater than 1, so again it cannot be the identity. Done!

By a result of Aleksandr Kurosh it follows that every modular subgroup is the group free product op copies of $C_2, C_3 $ or $C_{\infty} $ and we would like to determine the free generators explicitly for a cofinite subgroup starting from its associated Farey code associated to a special polygon corresponding to the subgroup.

To every even interval [tex]\xymatrix{x_i = \frac{a_i}{b_i} \ar@{-}[r]_{\circ} & x_{i+1}= \frac{a_{i+1}}{b_{i+1}}}[/tex] in the Farey code one associates the generator of a $C_2 $ component

$A_i = \begin{bmatrix} a_{i+1}b_{i+1}+ a_ib_i & -a_i^2-a_{i+1}^2 \\\ b_i^2+b_{i+1}^2 & -a_{i+1}b_{i+1}-a_ib_i \end{bmatrix} $

to every odd interval [tex]\xymatrix{x_i = \frac{a_i}{b_i} \ar@{-}[r]_{\bullet} & x_{i+1} = \frac{a_{i+1}}{b_{i+1}}}[/tex] in the Farey code we associate the generator of a $C_3 $ component

$B_i = \begin{bmatrix} a_{i+1}b_{i+1}+a_ib_{i+1}+a_ib_i & -a_i^2-a_ia_{i+1}-a_{i+1}^2 \\\ b_i^2+b_ib_{i+1} + b_{i+1}^2 & -a_{i+1}b_{i+1} – a_{i+1}b_i – a_i b_i \end{bmatrix} $

and finally, to every pair of free intervals [tex]\xymatrix{x_k \ar@{-}[r]_{a} & x_{k+1}} \ldots \xymatrix{x_l \ar@{-}[r]_{a} & x_{l+1}}[/tex] we associate the generator of a $C_{\infty} $ component

$C_{k,l} = \begin{bmatrix} a_l & -a_{l+1} \\\ b_l & – b_{l+1} \end{bmatrix} \begin{bmatrix} a_{k+1} & a_k \\\ b_{k+1} & b_k \end{bmatrix}^{-1} $

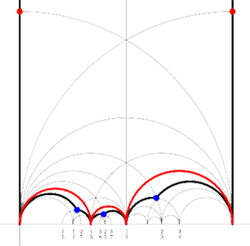Kulkarni’s result states that these matrices are free generators of the cofiniite modular subgroup determined by the Farey code. For example, for the M(12) special polygon on the left (bounded by the thick black geodesics), the Farey-code for this Mathieu polygon is

[tex]\xymatrix{\infty \ar@{-}[r]_{1} & 0 \ar@{-}[r]_{\bullet} & \frac{1}{3} \ar@{-}[r]_{\bullet} & \frac{1}{2} \ar@{-}[r]_{\bullet} & 1 \ar@{-}[r]_{1} & \infty}[/tex]

Therefore, the structure of the subgroup must be $C_{\infty} \ast C_3 \ast C_3 \ast C_3 $ with the generator of the infinite factor being

$\begin{bmatrix} -1 & 1 \\\ -1 & 0 \end{bmatrix} $ and those of the cyclic factors of order three

$\begin{bmatrix} 3 & -1 \\\ 13 & -4 \end{bmatrix}, \begin{bmatrix} 7 & -3 \\\ 19 & 8 \end{bmatrix} $ and $\begin{bmatrix} 4 & -3 \\\ 7 & -5 \end{bmatrix} $

This approach also gives another proof of the fact that $\Gamma = C_2 \ast C_3 $ because the Farey code to the subgroup of index 1 is [tex]\xymatrix{\infty \ar@{-}[r]_{\circ} & 0 \ar@{-}[r]_{\bullet} & \infty}[/tex] corresponding to the fundamental domain on the left. This finishes (for now) this thread on Kulkarni’s paper (or rather, part of it). On the Lost? page I will try to list threads in a logical ordering when they materialize.

Reference

Ravi S. Kulkarni, “An arithmetic-geometric method in the study of the subgroups of the modular group”, Amer. J. Math 113 (1991) 1053-1133

Hexagonal Moonshine (2)

Published July 11, 2007 by lieven

Delving into finite dimensional representations of the modular group $\Gamma = PSL_2(\mathbb{Z}) $ it is perhaps not too surprising to discover numerical connections with modular functions. Here, one such strange observation and a possible explanation.

Using the _fact_ that the modular group $\Gamma = PSL_2(\mathbb{Z}) $ is the free group product $C_2 \ast C_3 $ it is fairly easy to see that the variety of all n-dimensional representations $\mathbf{rep}_n~\Gamma $ is smooth (though it contains several connected components). Some of these components will contain simple representations, some will not. Anyway, we are not interested in all n-dimensional representations but in the isomorphism classes of such representations. The best algebraic approximation to this problem is by studying the quotient varieties

$\mathbf{iss}_n~\Gamma = \mathbf{rep}_n~\Gamma // GL(n) $

under the action of $GL(n) $ by basechange. Geometric invariant theory tells us that the points of this quotient variety correspond to isoclasses of semi-simple n-dimensional representations (whence the notation $\mathbf{iss}_n $). Again, these quotient varieties split into several connected components, some of which will have an open subset of points corresponding to simple representations.

It is a natural idea to compute the codimension of subvariety of proper semi-simples in the component of maximal dimension containing simple representations. _M-geometry_ allows you to reduce such calculation to quiver-problems. Anyway, if one does this for small values of n one obtains the following sequence of codimension-numbers (starting with $n=1 $

0,1,1,1,1,3,1,3,3,3,3,5,3,5,5,5,5,7,5,7,…

which doesnt seem too exciting before you feed it to Sloan’s integer sequences encyclopedia when one discovers that it is precisely sequence A063195 which gives the dimensions of weight 2n _cuspidal newforms_
for $\Gamma_0(6) $…

The optimistic “moonshine”-interpretation of this might be that these newforms can be viewed somehow as functions on the varieties of finite dimensional $\Gamma $-representations having the property that they pick out generic simple representations as their non-zeroes.

Be that as it may (one never knows in these matters), here a more down-to-earth explanation. The sequence A063195 obviously has a 6-periodicity behaviour so it suffices to understand why the codimension-sequence should have a similar feature (modulo computing the first few terms of it and observing the coincidence with the first few terms of A063195).

The modular group has exactly 6 one-dimensional representations and if one calculates their clan as in hexagonal moonshine (1) one obtains the hexagonal quiver

[tex]\xymatrix{& \vtx{S_1} \ar@/^/[dl] \ar@/^/[dr] & \\ \vtx{S_6} \ar@/^/[ur] \ar@/^/[d] & & \vtx{S_2} \ar@/^/[ul] \ar@/^/[d] \\ \vtx{S_5} \ar@/^/[u] \ar@/^/[dr] & & \vtx{S_3} \ar@/^/[u] \ar@/^/[dl] \\ & \vtx{S_4} \ar@/^/[ur] \ar@/^/[ul] & }[/tex]

M-geometry tells us that this clan contains enough information to determine the components of $\mathbf{rep}_n~\Gamma $ that contain simple representations. They correspond to dimension-vectors of this hexagonal quiver, say

$~(a_1,a_2,a_3,a_4,a_5,a_6) $

such that $a_i \leq a_{i-1}+a_{i+1} $. Moreover, the component is of maximal dimension if the components $a_i $ are evenly spread over the six vertices.
This then explains that the codimension sequence we are interested in must satisfy 6-periodicity.

Reference

This post corrects the erroneous statement made in math.AG/0610587 that the codimension sequence are the dimensions of weight 2n modular forms. The day the paper hit the arXiv I informed the author of the mistakes he made and told him how they could be corrected. Having waited 9 months I’ve given up hope that a revision/correction is imminent.