Last time we introduced the tangent quiver $\vec{t}~A $ of an affine algebra A to be a quiver on the isoclasses of simple finite dimensional representations. When $A=\mathbb{C}[X] $ is the coordinate ring of an affine variety, these vertices are just the points of the variety $X $ and this set has the extra structure of being endowed with the Zariski topology. For a general, possibly noncommutative algebra, we would like to equip the vertices of $\vec{t}~A $ also with a topology.
In the commutative case, the Zariski topology has as its closed sets the common zeroes of a set of polynomials on $X $, so we need to generalize the notion of ‘functions’ the the noncommutative world. The NC-mantra states that we should view the algebra A as the ring of functions on a (usually virtual) noncommutative space. And, face it, for a commutative variety $X $ the algebra $A=\mathbb{C}[X] $ does indeed do the job. Still, this is a red herring.
Let’s consider the easiest noncommutative case, that of the group algebra $\mathbb{C} G $ of a finite group $G $. In this case, the vertices of the tangent quiver $\vec{t}~A $ are the irreducible representations of $G $ and no sane person would consider the full group algebra to be the algebra of functions on this set. However, we do have a good alternative in this case : characters which allow us to separate the irreducibles and are a lot more manageable than the full group algebra. For example, if $G $ is the monster group then the group algebra has dimension approx $8 \times 10^{53} $ whereas there are just 194 characters to consider…
But, can we extend characters to arbitrary noncommutative algebras? and, more important, are there enough of these to separate the simple representations? The first question is easy enough to answer, after all characters are just traces so we can define for every element $a \in A $ and any finite dimensional simple A-representation $S $ the character
$\chi_a(S) = Tr(a | S) $
where $a | S $ is the matrix describing the action of a on S. But, you might say, characters are then just linear functionals on the algebra A so it is natural to view A as the function algebra, right? Wrong! Traces have the nice property that $Tr(ab)=Tr(ba) $ and so they vanish on all commutators $[a,b]=ab-ba $ of A, so characters only carry information of the quotient space
$\mathfrak{g}_A = \frac{A}{[A,A]_{vect}} $
where $[A,A]_{vect} $ is the vectorspace spanned by all commutators (and not the ideal…). If one is too focussed on commutative geometry one misses this essential simplification as clearly for $A=\mathbb{C}[X] $ being a commutative algebra,
$[\mathbb{C}[X],\mathbb{C}[X]]_{vect}=0 $ and therefore in this case $\mathfrak{g}_{\mathbb{C}[X]} = \mathbb{C}[X] $
Ok, but are there enough characters (that is, linear functionals on $\mathfrak{g}_A $, that is elements of the dual space $\mathfrak{g}_A^* $) to separate the simple representations? And, why do I (ab)use Lie-algebra notation $\mathfrak{g}_A $ to denote the vectorspace $A/[A,A]_{vect} $???
Leave a Comment Here, the vertex spaces on the left are the iso-typical factors of $V \downarrow_{D_2} $ and those on the right those of $V \downarrow_{D_3} $ and the arrows give the block-components of the $C_2 $-isomorphism $\phi $. The nice things is that one can also reverse this process to get all $\tilde{\Gamma} $-representations from $\theta $-semistable representations of this quiver (having the additional condition that the square matrix made of the arrows is invertible) and isomorphisms of group-representation correspond to those of quiver-representations!
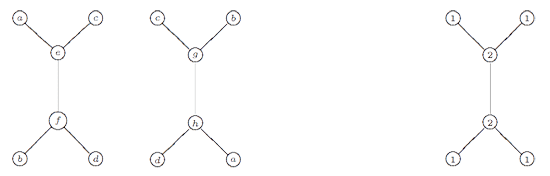
Here, the vertex spaces on the left are the iso-typical factors of $V \downarrow_{D_2} $ and those on the right those of $V \downarrow_{D_3} $ and the arrows give the block-components of the $C_2 $-isomorphism $\phi $. The nice things is that one can also reverse this process to get all $\tilde{\Gamma} $-representations from $\theta $-semistable representations of this quiver (having the additional condition that the square matrix made of the arrows is invertible) and isomorphisms of group-representation correspond to those of quiver-representations!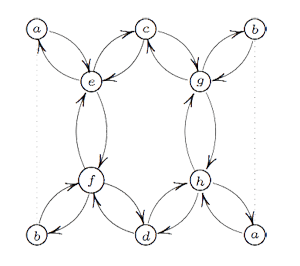 If one calculates the ‘clan’ of these 8 simples one obtains the double quiver of the graph on the left. Note that a and b appear twice, so one should glue the left and right hand sides together as a Moebius-strip. That is, the clan determining the representation theory of the extended modular group is a Moebius strip made of two hexagons!
If one calculates the ‘clan’ of these 8 simples one obtains the double quiver of the graph on the left. Note that a and b appear twice, so one should glue the left and right hand sides together as a Moebius-strip. That is, the clan determining the representation theory of the extended modular group is a Moebius strip made of two hexagons!