In the shape of languages we started from a collection of notes, made a poset of text-snippets from them, and turned this into an enriched category over the unit interval $[0,1]$, following the paper paper An enriched category theory of language: from syntax to semantics by Tai-Danae Bradley, John Terilla and Yiannis Vlassopoulos.
This allowed us to view the text-snippets as points in a Lawvere pseudoquasi metric space, and to define a ‘topos’ of enriched presheaves on it, including the Yoneda-presheaves containing semantic information of the snippets.
In the previous post we looked at ‘building a second brain’ apps, such as LogSeq and Obsidian, and hoped to use them to test the conjectured ‘topos of the unconscious’.
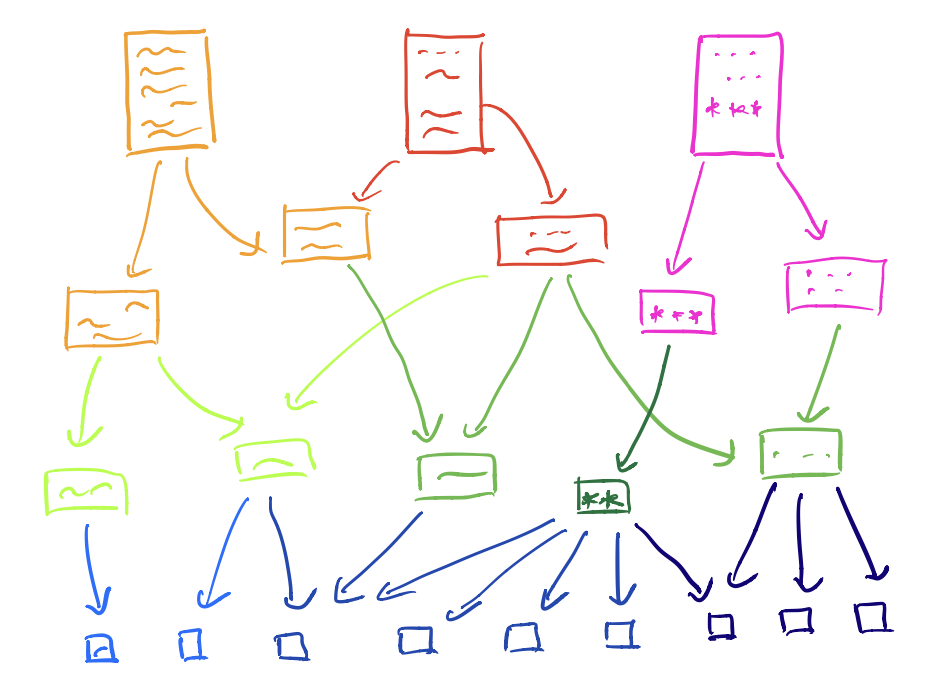
In Obsidian, a vault is a collection of notes (with their tags and other meta-data), together with all links between them.
The vault of the language-poset will have one note for every text-snipped, and have a link from note $n$ to note $m$ if $m$ is a text-fragment in $n$.
In their paper, Bradley, Terilla and Vlassopoulos use the enrichment structure where $\mu(n,m) \in [0,1]$ is the conditional probablity of the fragment $m$ to be extended to the larger text $n$.
Most Obsidian vaults are a lot more complicated, possibly having oriented cycles in their internal link structure.
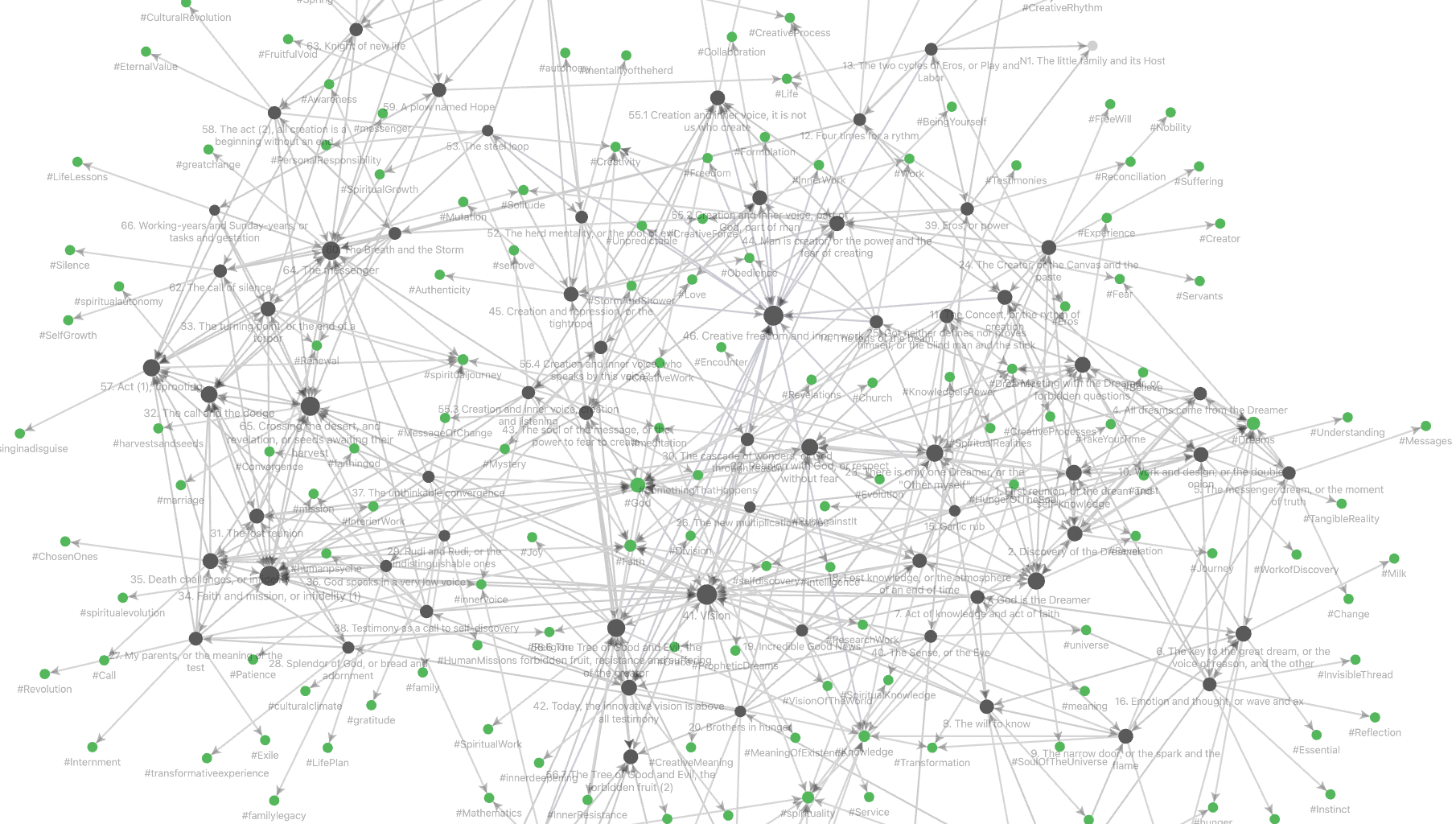
Still, it is always possible to turn the notes of the vault into a category enriched over $[0,1]$, in multiple ways, depending on whether we want to focus on the internal link-structure or rather on the semantic similarity between notes, or any combination of these.
Let $X$ be a set of searchable data from your vault. Elements of $X$ may be
- words contained in notes
- in- or out-going links between notes
- tags used
- YAML-frontmatter
- …
Assign a positive real number $r_x \geq 0$ to every $x \in X$. We see $r_x$ as the ‘relevance’ we attach to the search term $x$. So, it is possible to emphasise certain key-words or tags, find certain links more important than others, and so on.
For this relevance function $r : X \rightarrow \mathbb{R}_+$, we have a function defined on all subsets $Y$ of $X$
$$f_r~:~\mathcal{P}(X) \rightarrow \mathbb{R}_+ \qquad Y \mapsto f_r(Y) = \sum_{x \in Y} r_x$$
Take a note $n$ from the vault $V$ and let $X_n$ be the set of search terms from $X$ contained in $n$.
We can then define a (generalised) Jaccard distance for any pair of notes $n$ and $m$ in $V$:
$$ d_r(n,m) = \begin{cases}
0~\text{if $f_r(X_n \cup X_m)=0$} \\ 1-\frac{f_r(X_n \cap X_m)}{f_r(X_n \cup X_m)}~\text{otherwise} \end{cases}$$
This distance is symmetric, $d_r(n,n)=0$ for all notes $n$, and the crucial property is that it satisfies the triangle inequality, that is, for all triples of notes $l$, $m$ and $n$ we have
$$d_r(l,n) \leq d_r(l,m)+d_r(m,n)$$
For a proof in this generality see the paper A note on the triangle inequality for the Jaccard distance by Sven Kosub.
How does this help to make the vault $V$ into a category enriched over $[0,1]$?
The poset $([0,1],\leq)$ is the category with objects all numbers $a \in [0,1]$, and a unique morphism $a \rightarrow b$ between two numbers iff $a \leq b$. This category has limits (infs) and colimits (sups), has a monoidal structure $a \otimes b = a \times b$ with unit object $1$, and an internal hom
$$Hom_{[0,1]}(a,b) = (a,b) = \begin{cases} \frac{b}{a}~\text{if $b \leq a$} \\ 1~\text{otherwise} \end{cases}$$

We say that the vault is an enriched category over $[0,1]$ if for every pair of notes $n$ and $m$ we have a number $\mu(n,m) \in [0,1]$ satisfying for all notes $n$
$$\mu(n,n)=1~\quad~\text{and}~\quad~\mu(m,l) \times \mu(n,m) \leq \mu(n,l)$$
for all triples of notes $l,m$ and $n$.
Starting from any relevance function $r : X \rightarrow \mathbb{R}_+$ we define for every pair $n$ and $m$ of notes the distance function $d_r(m,n)$ satisfying the triangle inequality. If we now take
$$\mu_r(m,n) = e^{-d_r(m,n)}$$
then the triangle inequality translates for every triple of notes $l,m$ and $n$ into
$$\mu_r(m,l) \times \mu_r(n,m) \leq \mu_r(n,l)$$
That is, every relevance function makes $V$ into a category enriched over $[0,1]$.
Two simple relevance functions, and their corresponding distance and enrichment functions are available from Obsidian’s Graph Analysis community plugin.
To get structural information on the link-structure take as $X$ the set of all incoming and outgoing links in your vault, with relevance function the constant function $1$.
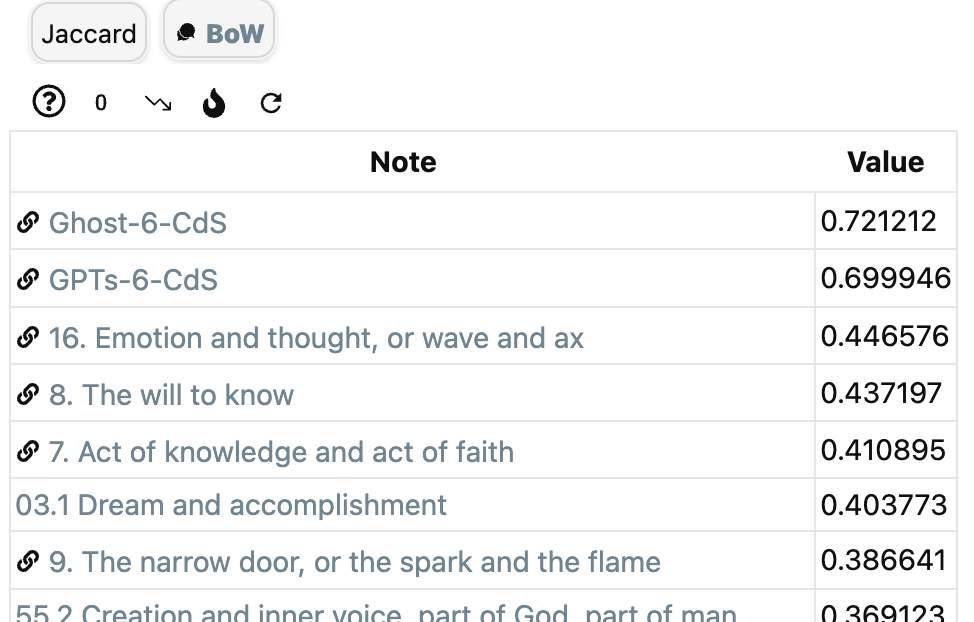
‘Jaccard’ in Graph Analysis computes for the current note $n$ the value of $1-d_r(n,m)$ for all notes $m$, so if this value is $a \in [0,1]$, then the corresponding enrichment value is $\mu_r(m,n)=e^{a-1}$.
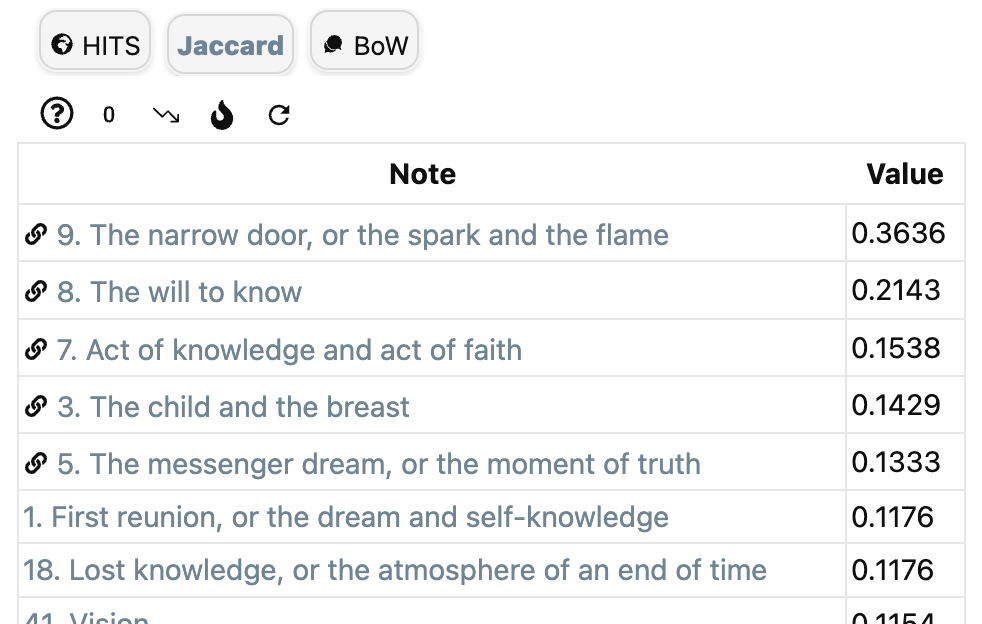
To get semantic information on the similarity between notes, let $X$ be the set of all words in all notes and take again as relevance function the constant function $1$.
To access ‘BoW’ (Bags of Words) in Graph Analysis, you must first install the (non-community) NLP plugin which enables various types of natural language processing in the vault. The install is best done via the BRAT plugin (perhaps I’ll do a couple of posts on Obsidian someday).
If it gives for the current note $n$ the value $a$ for a note $m$, then again we can take as the enrichment structure $\mu_r(n,m)=e^{a-1}$.
Graph Analysis offers more functionality, and a good introduction is given in this clip:
Calculating the enrichment data for custom designed relevance functions takes a lot more work, but is doable. Perhaps I’ll return to this later.
Mathematically, it is probably more interesting to start with a given enrichment structure $\mu$ on the vault $V$, describe the category of all enriched presheaves $\widehat{V_{\mu}}$ and find out what we can do with it.
(tbc)
Previously in this series:
Next:
The super-vault of missing notes
Comments closed