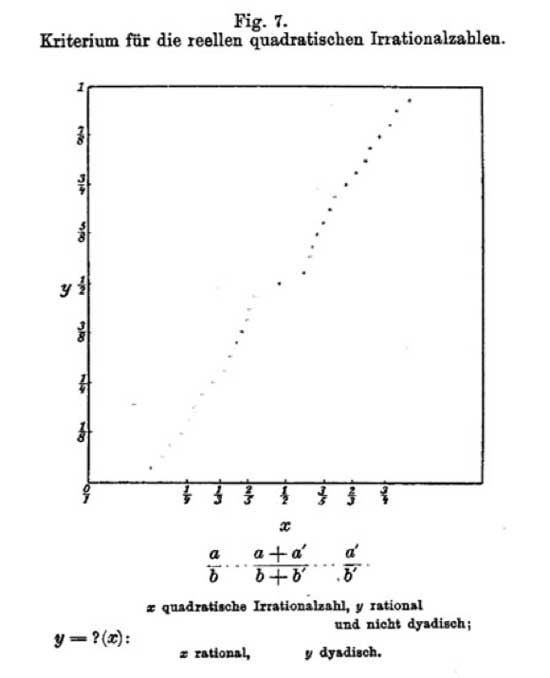
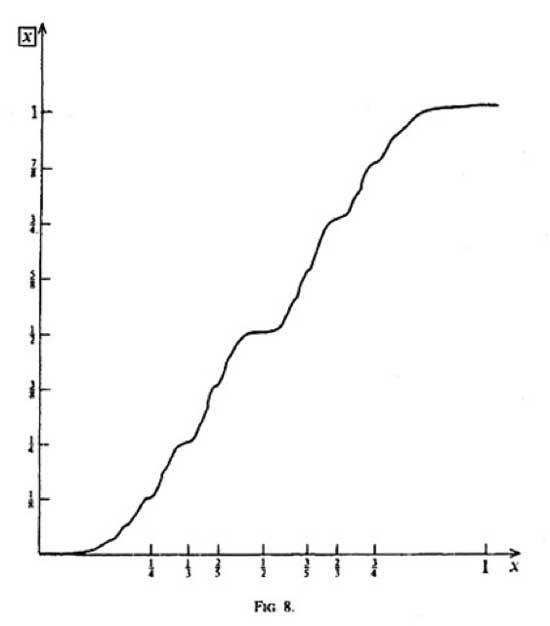
Here a list of pdf-files of NeverEndingBooks-posts on general topics, in reverse chronological order.
Leave a CommentTag: LaTeX
- No math
- today. If you’re interested in the latest on noncommutative geometry,
- head over to the NCG-blog where Alain Connes has a post on
- Time.
- Still, Alain’s post is a good illustration of what Ill be rambling about
- TeX and how to use it in a blog.
If you’re running a math-blog,
sooner or later you want to say something more than new-age speak like
‘points talking to each other’ and get to the essence of it. In short,
you want to talk math and it’s a regrettable fact that math doesnt go
well with ASCII. In everyday life we found a way around this : we all
use TeX to write papers and even email-wise (among mathematicians) we
write plain TeX-commands as this language is more common to us than
English. But, plain TeX and the blogosphere don’t mix well. If you’re
expecting only professional mathematicians to read what you write, you
might as well arXiv your thoughts. Im convinced the majority of people
coming here (for whatever reason) dont speak plain-TeX. Fortunately,
there is technology to display TeX-symbols on a blog. Personally, I was
an early adapter to
LaTeXRender and even today a
fair share of page-views relates to the few
posts I did on
how to get latexrender working on a mac. Some time ago I
switched to mathML and now I’m
regretting I ever did…
Mind you, I’m convinced that mathML is the
‘proper’ way to get TeX to the internet but there are at the moment some
serious drawbacks. For starters, it is highly user-unfriendly. You
simply cannot expect people to switch browsers (as well as installing
extra fonts) just because they come to your site (or you have to be a
pretty arrogant git). Speaking for myself, Im still having (against my
better judgment) Safari as my default browser, so when I come to a site
like the n-category cafe I just
skim the plain-text in between and if (and only if) the topic interests
me tremendously I’ll allow myself to switch to Flock or Firefox to read
the post in detail. I’m convinced most of you have a similar
surfing-attitude. MathML also has serious consequences on the
server-side. If you want to serve mathML you have to emit headers which
expect everything to follow to be purified XHTML. If I ever forget a
closing tag in a post, this is enough to break down NeverEndingBooks to
all Firefox-users. I’ve been writing HTML since the times when the best
browser around was something called NCSA Mosaic so Ive a
pretty lax attitude to end-tags (especially in IMG-tags) and Im just
getting too old to change these bad habbits now… It seems I’m not the
only one. Many developers of WordPress-plugins write bad XHTML-code, so
the last couple of weeks I’ve been spending more time fixing up code
than writing posts. If you want to run a mathML-wordpress site you might
find the following hints helpfull. If you get a ‘yellow screen of
death’ when viewing your site with Firefox, chances are that one of your
plugin-authors missed a closing tag in the HTML-rendering of his/her
plugin. As a rule of thumb : go for the IMG-tags first! I’m sorry to
say, but Latexrender-Steve
is among the XHTML-offenders. (On a marginal note, LaTeXrender also has
its drawbacks : to mathematicians this may seem incredible but what
Latexrender does to get one expression displayed is to TeX an entire
file, get the image from the ps-file turn it into a gif and display it,
so one gets a GIF-folder of enrmous proportions. Hence, use Latexrender
only if you have your own server and dont have to care about memory
constraints. Another disadvantedge was that the GIFs were displayed with
a vertical offset, but this has been solved recently (use the ‘offset
beta’ files in the distribution)). Wrt. to that offset-beta version, use
this latex.php file instead (I
changed the IMG-line). Some plugins may not serve the correct headers
to display mathML. So, if you want to allow readers to have a
printer-friendly version of your mathML-post, get the WP-print plugin BUT
change to this wp-print.php file in order to
send the proper headers. Sometimes there are just forgotten lines/tags
in the code, such as in the [future calendar plugin](http://anthologyoi.com/wordpress/plugins/future-posts-calendar-
plugin.html). So, please use this version
of the future.calendar.php file. And so on, and so on. The joys of
trying to maintain a mathML-based blog… So, no surprise I’m seriously
considering to ditch mathML and change to normal headers soon. One of
the things I like about LaTeXRender is that it can be extended, meaning
that you can get your own definitions and packages loaded whereas with
mathML you’re bound to write iTeX, which Ill never manage. But, again,
mathML will be the correct technology once all major browsers are mathML
capable and the font-problem is resolved. Does anyone know whether
Safari 3 (in Leopard, that is Mac OS 10.5 to the rest of you) will be
mathML-able?


 What concerns
What concerns