Skip to content →

Tag: hyperbolic

Superpotentials and Calabi-Yaus

Published December 22, 2007 by lieven

Yesterday, Jan Stienstra gave a talk at theARTS entitled “Quivers, superpotentials and Dimer Models”. He started off by telling that the talk was based on a paper he put on the arXiv Hypergeometric Systems in two Variables, Quivers, Dimers and Dessins d’Enfants but that he was not going to say a thing about dessins but would rather focuss on the connection with superpotentials instead…pleasing some members of the public, while driving others to utter despair.

Anyway, it gave me the opportunity to figure out for myself what dessins might have to do with dimers, whathever these beasts are. Soon enough he put on a slide containing the definition of a dimer and from that moment on I was lost in my own thoughts… realizing that a dessin d’enfant had to be a dimer for the Dedekind tessellation of its associated Riemann surface!
and a few minutes later I could slap myself on the head for not having thought of this before :

There is a natural way to associate to a Farey symbol (aka a permutation representation of the modular group) a quiver and a superpotential (aka a necklace) defining (conjecturally) a Calabi-Yau algebra! Moreover, different embeddings of the cuboid tree diagrams in the hyperbolic plane may (again conjecturally) give rise to all sorts of arty-farty fanshi-wanshi dualities…

I’ll give here the details of the simplest example I worked out during the talk and will come back to general procedure later, when I’ve done a reference check. I don’t claim any originality here and probably all of this is contained in Stienstra’s paper or in some physics-paper, so if you know of a reference, please leave a comment. Okay, remember the Dedekind tessellation ?

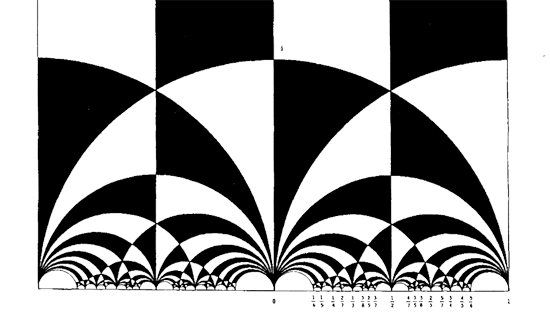
So, all hyperbolic triangles we will encounter below are colored black or white. Now, take a Farey symbol and consider its associated special polygon in the hyperbolic plane. If we start with the Farey symbol

[tex]\xymatrix{\infty \ar@{-}_{(1)}[r] & 0 \ar@{-}_{\bullet}[r] & 1 \ar@{-}_{(1)}[r] & \infty} [/tex]

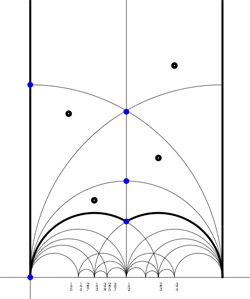we get the special polygonal region bounded by the thick edges, the vertical edges are identified as are the two bottom edges. Hence, this fundamental domain has 6 vertices (the 5 blue dots and the point at $i \infty $) and 8 hyperbolic triangles (4 colored black, indicated by a black dot, and 4 white ones).

Right, now let us associate a quiver to this triangulation (which embeds the quiver in the corresponding Riemann surface). The vertices of the triangulation are also the vertices of the quiver (so in our case we are going for a quiver with 6 vertices). Every hyperbolic edge in the triangulation gives one arrow in the quiver between the corresponding vertices. The orientation of the arrow is determined by the color of a triangle of which it is an edge : if the triangle is black, we run around its edges counter-clockwise and if the triangle is white we run over its edges clockwise (that is, the orientation of the arrow is independent of the choice of triangles to determine it). In our example, there is one arrows directed from the vertex at $i $ to the vertex at $0 $, whether you use the black triangle on the left to determine the orientation or the white triangle on the right. If we do this for all edges in the triangulation we arrive at the quiver below

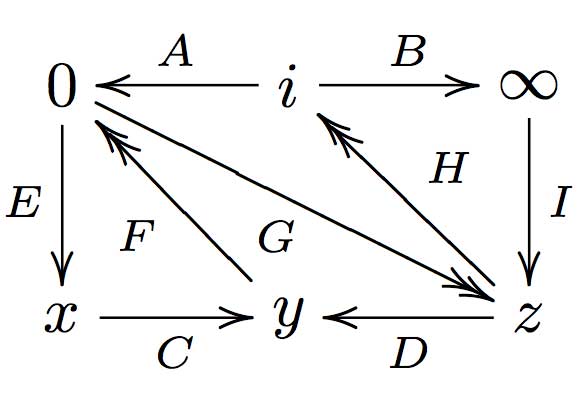
where x,y and z are the three finite vertices on the $\frac{1}{2} $-axis from bottom to top and where I’ve used the physics-convention for double arrows, that is there are two F-arrows, two G-arrows and two H-arrows. Observe that the quiver is of Calabi-Yau type meaning that there are as much arrows coming into a vertex as there are arrows leaving the vertex.

Now that we have our quiver we determine the superpotential as follows. Fix an orientation on the Riemann surface (for example counter-clockwise) and sum over all black triangles the product of the edge-arrows counterclockwise MINUS sum over all white triangles
the product of the edge arrows counterclockwise. So, in our example we have the cubic superpotential

$IH’B+HAG+G’DF+FEC-BHI-H’G’A-GFD-CEF’ $

From this we get the associated noncommutative algebra, which is the quotient of the path algebra of the above quiver modulo the following ‘commutativity relations’

$\begin{cases} GH &=G’H’ \\ IH’ &= IH \\ FE &= F’E \\ F’G’ &= FG \\ CF &= CF’ \\ EC &= GD \\ G’D &= EC \\ HA &= DF \\ DF’ &= H’A \\ AG &= BI \\ BI &= AG’ \end{cases} $

and morally this should be a Calabi-Yau algebra (( can someone who knows more about CYs verify this? )). This concludes the walk through of the procedure. Summarizing : to every Farey-symbol one associates a Calabi-Yau quiver and superpotential, possibly giving a Calabi-Yau algebra!

Leave a Comment

the iguanodon dissected

Published November 9, 2007 by lieven

Here the details of the iguanodon series. Start with the Farey sequence $F(n) $of order n which is the sequence of completely reduced fractions between 0 and 1 which, when in lowest terms, have denominators less than or equal to n, arranged in order of increasing size. Here are the first eight Fareys

F(1) = {0โ„1, 1โ„1}
F(2) = {0โ„1, 1โ„2, 1โ„1}
F(3) = {0โ„1, 1โ„3, 1โ„2, 2โ„3, 1โ„1}
F(4) = {0โ„1, 1โ„4, 1โ„3, 1โ„2, 2โ„3, 3โ„4, 1โ„1}
F(5) = {0โ„1, 1โ„5, 1โ„4, 1โ„3, 2โ„5, 1โ„2, 3โ„5, 2โ„3, 3โ„4, 4โ„5, 1โ„1}
F(6) = {0โ„1, 1โ„6, 1โ„5, 1โ„4, 1โ„3, 2โ„5, 1โ„2, 3โ„5, 2โ„3, 3โ„4, 4โ„5, 5โ„6, 1โ„1}
F(7) = {0โ„1, 1โ„7, 1โ„6, 1โ„5, 1โ„4, 2โ„7, 1โ„3, 2โ„5, 3โ„7, 1โ„2, 4โ„7, 3โ„5, 2โ„3, 5โ„7, 3โ„4, 4โ„5, 5โ„6, 6โ„7, 1โ„1}
F(8) = {0โ„1, 1โ„8, 1โ„7, 1โ„6, 1โ„5, 1โ„4, 2โ„7, 1โ„3, 3โ„8, 2โ„5, 3โ„7, 1โ„2, 4โ„7, 3โ„5, 5โ„8, 2โ„3, 5โ„7, 3โ„4, 4โ„5, 5โ„6, 6โ„7, 7โ„8, 1โ„1}

Farey sequences have plenty of mysterious properties. For example, in 1924 J. Franel and Edmund Landau proved that an asymptotic density result about Farey sequences is equivalent to the Riemann hypothesis.
More precisely, let a(n) be the number of terms in the Farey sequence F(n) (that is, a(1)=2,a(2)=3,…,a(8)=23 etc. This is sequence A005728 in the online integer sequences catalog).
Let $F(n)_j $ denote the j-th term in F(n), then the following conjecture is equivalent to the Riemann hypothesis

For every $\epsilon > 0 $ there is a constant C depending on $\epsilon $ such that

$\sum_{j=1}^{a(n)} | F(n)_j – \frac{j}{a(n)} | < C n^{\frac{1}{2}+\epsilon} $

when n goes to infinity. Anyway, let us continue our construction. Farey sequences are clearly symmetric around 1/2 so let us just take half of them, so we jump to 1 when we have reached 1/2. Let us extend this halved Farey on both sides with $\infty $ and call it the modified Farey sequence f(n). For example,

$f(3) = {~\infty,0,\frac{1}{3},\frac{1}{2},1,\infty } $

Now consider the Farey code in which we identify the two sides connected to $\infty $ and mark two consecutive Farey numbers as

[tex]\xymatrix{f(n)_i \ar@{-}[r]_{\bullet} & f(n)_{i+1}}[/tex]

That is, the Farey code associated to the modified sequence f(3) is

[tex]\xymatrix{\infty \ar@{-}[r]_{1} & 0 \ar@{-}[r]_{\bullet} & \frac{1}{3} \ar@{-}[r]_{\bullet} & \frac{1}{2} \ar@{-}[r]_{\bullet} & 1 \ar@{-}[r]_{1} & \infty}[/tex]

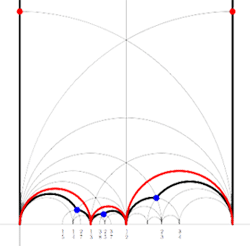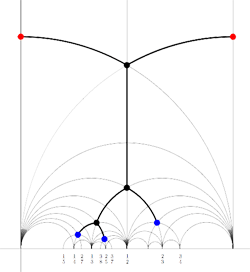
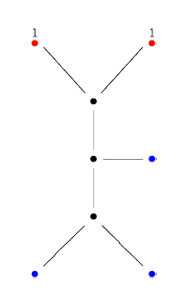
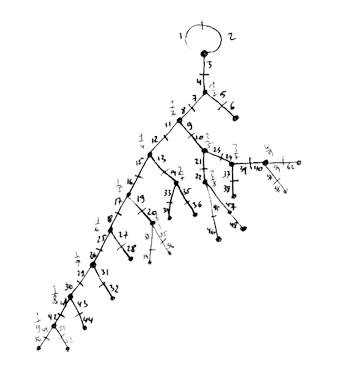
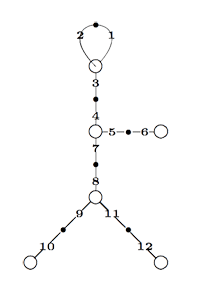Recall from earlier that to a Farey-code we can associate a special polygon by first taking the hyperbolic convex hull of all the terms in the sequence (the region bounded by the vertical lines and the bottom red circles in the picture on the left) and adding to it for each odd interval [tex]\xymatrix{f(n)_i \ar@{-}[r]_{\bullet} & f(n)_{i+1}}[/tex] the triangle just outside the convex hull consisting of two odd edges in the Dedekind tessellation (then we obtain the region bounded by the black geodesics for the sequence f(3)).

Next, we can associate to this special polygon a cuboid tree diagram by considering all even and odd vertices on the boundary (which are tinted red, respectively blue) together with all odd vertices in the interior of the special polygon. These are indicated in the left picture below. If we connect these vertices with the geodesics in the polygon we get a cuboid tree diagram. The obtained cuboid tree diagram is depicted on the right below.

Finally, identifying the red points (as they lie on geodesics connected to $\infty $ which are identified in the Farey code), adding even points on the remaining geodesics and numbering the obtained half-lines we obtain the dessin d’enfant given on the left hand side. To such a dessin we can associate its monodromy group which is a permutation group on the half-lines generated by an order two element indicating which half-lines make up a line and an order three element indicating which half-lines one encounters by walking counter-clockwise around a three-valent vertex. For the dessin on the left the group is therefore the subgroup of $S_{12} $ generated by the elements

$\alpha = (1,2)(3,4)(5,6)(7,8)(9,10)(11,12) $

$\beta = (1,2,3)(4,5,7)(8,9,11) $

and a verification with GAP tells us that this group is the sporadic Mathieu group $M_{12} $. This concludes the description of the second member of the Iguanodon series. If you like to check that the first 8 iguanodons are indeed the simple groups

$L_2(7), M_{12}, A_{16}, M_{24}, A_{28}, A_{40}, A_{48}, A_{60}, \ldots $

the following dissection of the Iguanodon may prove useful

Leave a Comment

Mathieuโ€™s blackjack (3)

Published July 17, 2007 by lieven

If you only tune in now, you might want to have a look at the definition of Mathieu’s blackjack and the first part of the proof of the Conway-Ryba winning strategy involving the Steiner system S(5,6,12) and the Mathieu sporadic group $M_{12} $.

We’re trying to disprove the existence of misfits, that is, of non-hexad positions having a total value of at least 21 such that every move to a hexad would increase the total value. So far, we succeeded in showing that such a misfit must have the patern

$\begin{array}{|c|ccc|} \hline 6 & III & \ast & 9 \\ 5 & II & 7 & . \\ IV & I & 8 & . \\ \hline & & & \end{array} $

That is, a misfit must contain the 0-card (queen) and cannot contain the 10 or 11(jack) and must contain 3 of the four Romans. Now we will see that a misfit also contains precisely one of {5,6} (and consequently also exactly one card from {7,8,9}). To start, it is clear that it cannot contain BOTH 5 and 6 (then its total value can be at most 20). So we have to disprove that a misfit can miss {5,6} entirely (and so the two remaining cards (apart from the zero and the three Romans) must all belong to {7,8,9}).

Lets assume the misfit misses 5 and 6 and does not contain 9. Then, it must contain 4 (otherwise, its column-distribution would be (0,3,3,0) and it would be a hexad). There are just three such positions possible

$\begin{array}{|c|ccc|} \hline . & \ast & \ast & . \\ . & \ast & \ast & . \\ \ast & . & \ast & . \\ \hline – & – & ? & ? \end{array} $ $\begin{array}{|c|ccc|} \hline . & \ast & \ast & . \\ . & . & \ast & . \\ \ast & \ast & \ast & . \\ \hline – & + & ? & ? \end{array} $ $\begin{array}{|c|ccc|} \hline . & . & \ast & . \\ . & \ast & \ast & . \\ \ast & \ast & \ast & . \\ \hline – & 0 & ? & ? \end{array} $

Neither of these can be misfits though. In the first one, there is an 8->5 move to a hexad of smaller total value (in the second a 7->5 move and in the third a 7->6 move). Right, so the 9 card must belong to a misfit. Assume it does not contain the 4-card, then part of the misfit looks like (with either a 7- or an 8-card added)

$\begin{array}{|c|ccc|} \hline . & \ast & \ast & \ast \\ . & \ast & ? & . \\ . & \ast & ? & . \\ \hline & & & \end{array} $ contained in the unique hexad $\begin{array}{|c|ccc|} \hline \ast & \ast & \ast & \ast \\ . & \ast & & . \\ . & \ast & & . \\ \hline & & & \end{array} $

Either way the moves 7->6 or 8->6 decrease the total value, so it cannot be a misfit. Therefore, a misfit must contain both the 4- and 9-card. So it is of the form on the left below

$\begin{array}{|c|ccc|} \hline . & ? & \ast & \ast \\ . & ? & ? & . \\ \ast & ? & ? & . \\ \hline & & & \end{array} $ $\begin{array}{|c|ccc|} \hline . & . & \ast & . \\ . & \ast & \ast & \ast \\ \ast & \ast & . & . \\ \hline – & 0 & – & + \end{array} $ $\begin{array}{|c|ccc|} \hline . & . & \ast & \ast \\ . & \ast & \ast & . \\ \ast & \ast & . & . \\ \hline & & & \end{array} $

If this is a genuine misfit only the move 9->10 to a hexad is possible (the move 9->11 is not possible as all BUT ONE of {0,1,2,3,4} is contained in the misfit). Now, the only hexad containing 0,4,10 and 2 from {1,2,3} is in the middle, giving us what the misfit must look like before the move, on the right. Finally, this cannot be a misfit as the move 7->5 decreases the total value.

That is, we have proved the claim that a misfit must contain one of {5,6} and one of {7,8,9}. Right, now we can deliver the elegant finishing line of the Kahane-Ryba proof. A misfit must contain 0 and three among {1,2,3,4} (let us call the missing card s), one of $5+\epsilon $ with $0 \leq \epsilon \leq 1 $ and one of $7+\delta $ with $0 \leq \delta \leq 2 $. Then, the total value of the misfit is

$~(0+1+2+3+4-s)+(5+\epsilon)+(7+\delta)=21+(1+\delta+\epsilon-s) $

So, if this value is strictly greater than 21 (and we will see in a moment is has to be if it is at least 21) then we deduce that $s < 1 + \delta + \epsilon \leq 4 $. Therefore $1+\delta+\epsilon $ belongs to the misfit. But then the move $1+\delta \epsilon \rightarrow s $ moves the misfit to a 6-tuple with total value 21 and hence (as we see in a moment) must be a hexad and hence this is a decreasing move! So, finally, there are no misfits!

Hence, from every non-hexad pile of total value at least 21 we have a legal move to a hexad. Because the other player cannot move from an hexad to another hexad we are done with our strategy provided we can show (a) that the total value of any hexad is at least 21 and (b) that ALL 6-piles of total value 21 are hexads. As there are only 132 hexads it is easy enough to have their sum-distribution. Here it is

That is, (a) is proved by inspection and we see that there are 11 hexads of sum 21 (the light hexads in Conway-speak) and there are only 11 ways to get 21 as a sum of 6 distinct numbers from {0,1,..,11} so (b) follows. Btw. the obvious symmetry of the sum-distribution is another consequence of the duality t->11-t discussed briefly at the end of part 2.

Clearly, I’d rather have conceptual proofs for all these facts and briefly tried my hand. Luckily I did spot the following phrase on page 326 of Conway-Sloane (discussing the above distribution) :

“It will not be easy to explain all the above observations. They are certainly connected with hyperbolic geometry and with the ‘hole’ structure of the Leech lattice.”

So, I’d better leave it at this…

References

Joseph Kahane and Alexander J. Ryba, “The hexad game“

John H. Conway and N. J.A. Sloane, “Sphere packings, Lattices and Groups” chp. 11 ‘The Golay codes and the Mathieu groups’

Continue readingMathieuโ€™s blackjack (3)
Leave a Comment