Last time we tried to generalize the Connes-Consani approach to commutative algebraic geometry over the field with one element $\mathbb{F}_1 $ to the noncommutative world by considering covariant functors
$N~:~\mathbf{groups} \rightarrow \mathbf{sets} $
which over $\mathbb{C} $ resp. $\mathbb{Z} $ become visible by a complex (resp. integral) algebra having suitable universal properties.
However, we didn’t specify what we meant by a complex noncommutative variety (resp. an integral noncommutative scheme). In particular, we claimed that the $\mathbb{F}_1 $-‘points’ associated to the functor
$D~:~\mathbf{groups} \rightarrow \mathbf{sets} \qquad G \mapsto G_2 \times G_3 $ (here $G_n $ denotes all elements of order $n $ of $G $)
were precisely the modular dessins d’enfants of Grothendieck, but didn’t give details. We’ll try to do this now.
For algebras over a field we follow the definition, due to Kontsevich and Soibelman, of so called “noncommutative thin schemes”. Actually, the thinness-condition is implicit in both Soule’s-approach as that of Connes and Consani : we do not consider R-points in general, but only those of rings R which are finite and flat over our basering (or field).
So, what is a noncommutative thin scheme anyway? Well, its a covariant functor (commuting with finite projective limits)
$\mathbb{X}~:~\mathbf{Alg}^{fd}_k \rightarrow \mathbf{sets} $
from finite-dimensional (possibly noncommutative) $k $-algebras to sets. Now, the usual dual-space operator gives an anti-equivalence of categories
$\mathbf{Alg}^{fd}_k \leftrightarrow \mathbf{Coalg}^{fd}_k \qquad A=C^* \leftrightarrow C=A^* $
so a thin scheme can also be viewed as a contra-variant functor (commuting with finite direct limits)
$\mathbb{X}~:~\mathbf{Coalg}^{fd}_k \rightarrow \mathbf{Sets} $
In particular, we are interested to associated to any {tex]k $-algebra $A $ its representation functor :
$\mathbf{rep}(A)~:~\mathbf{Coalg}^{fd}_k \rightarrow \mathbf{Sets} \qquad C \mapsto Alg_k(A,C^*) $
This may look strange at first sight, but $C^* $ is a finite dimensional algebra and any $n $-dimensional representation of $A $ is an algebra map $A \rightarrow M_n(k) $ and we take $C $ to be the dual coalgebra of this image.
Kontsevich and Soibelman proved that every noncommutative thin scheme $\mathbb{X} $ is representable by a $k $-coalgebra. That is, there exists a unique coalgebra $C_{\mathbb{X}} $ (which they call the coalgebra of ‘distributions’ of $\mathbb{X} $) such that for every finite dimensional $k $-algebra $B $ we have
$\mathbb{X}(B) = Coalg_k(B^*,C_{\mathbb{X}}) $
In the case of interest to us, that is for the functor $\mathbf{rep}(A) $ the coalgebra of distributions is Kostant’s dual coalgebra $A^o $. This is the not the full linear dual of $A $ but contains only those linear functionals on $A $ which factor through a finite dimensional quotient.
So? You’ve exchanged an algebra $A $ for some coalgebra $A^o $, but where’s the geometry in all this? Well, let’s look at the commutative case. Suppose $A= \mathbb{C}[X] $ is the coordinate ring of a smooth affine variety $X $, then its dual coalgebra looks like
$\mathbb{C}[X]^o = \oplus_{x \in X} U(T_x(X)) $
the direct sum of all universal (co)algebras of tangent spaces at points $x \in X $. But how do we get the variety out of this? Well, any coalgebra has a coradical (being the sun of all simple subcoalgebras) and in the case just mentioned we have
$corad(\mathbb{C}[X]^o) = \oplus_{x \in X} \mathbb{C} e_x $
so every point corresponds to a unique simple component of the coradical. In the general case, the coradical of the dual coalgebra $A^o $ is the direct sum of all simple finite dimensional representations of $A $. That is, the direct summands of the coalgebra give us a noncommutative variety whose points are the simple representations, and the remainder of the coalgebra of distributions accounts for infinitesimal information on these points (as do the tangent spaces in the commutative case).
In fact, it was a surprise to me that one can describe the dual coalgebra quite explicitly, and that $A_{\infty} $-structures make their appearance quite naturally. See this paper if you’re in for the details on this.
That settles the problem of what we mean by the noncommutative variety associated to a complex algebra. But what about the integral case? In the above, we used extensively the theory of Kostant-duality which works only for algebras over fields…
Well, not quite. In the case of $\mathbb{Z} $ (or more general, of Dedekind domains) one can repeat Kostant’s proof word for word provided one takes as the definition of the dual $\mathbb{Z} $-coalgebra
of an algebra (which is $\mathbb{Z} $-torsion free)
$A^o = { f~:~A \rightarrow \mathbb{Z}~:~A/Ker(f)~\text{is finitely generated and torsion free}~} $
(over general rings there may be also variants of this duality, as in Street’s book an Quantum groups). Probably lots of people have come up with this, but the only explicit reference I have is to the first paper I’ve ever written. So, also for algebras over $\mathbb{Z} $ we can define a suitable noncommutative integral scheme (the coradical approach accounts only for the maximal ideals rather than all primes, but somehow this is implicit in all approaches as we consider only thin schemes).
Fine! So, we can make sense of the noncommutative geometrical objects corresponding to the group-algebras $\mathbb{C} \Gamma $ and $\mathbb{Z} \Gamma $ where $\Gamma = PSL_2(\mathbb{Z}) $ is the modular group (the algebras corresponding to the $G \mapsto G_2 \times G_3 $-functor). But, what might be the points of the noncommutative scheme corresponding to $\mathbb{F}_1 \Gamma $???
Well, let’s continue the path cut out before. “Points” should correspond to finite dimensional “simple representations”. Hence, what are the finite dimensional simple $\mathbb{F}_1 $-representations of $\Gamma $? (Or, for that matter, of any group $G $)
Here we come back to Javier’s post on this : a finite dimensional $\mathbb{F}_1 $-vectorspace is a finite set. A $\Gamma $-representation on this set (of n-elements) is a group-morphism
$\Gamma \rightarrow GL_n(\mathbb{F}_1) = S_n $
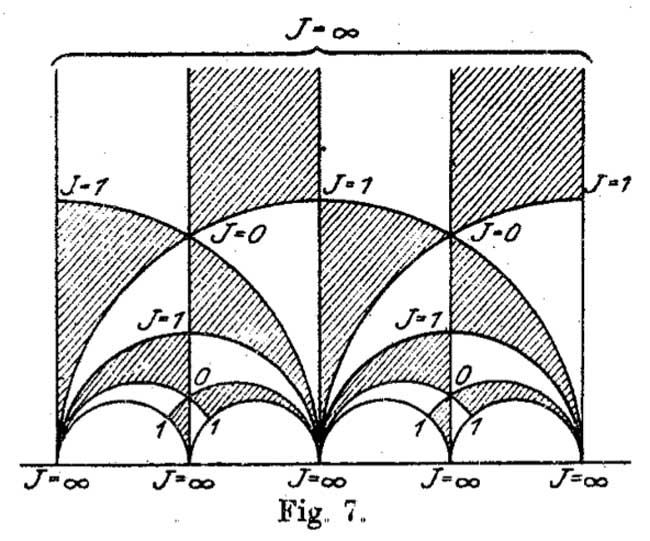
hence it gives a permutation representation of $\Gamma $ on this set. But then, if finite dimensional $\mathbb{F}_1 $-representations of $\Gamma $ are the finite permutation representations, then the simple ones are the transitive permutation representations. That is, the points of the noncommutative scheme corresponding to $\mathbb{F}_1 \Gamma $ are the conjugacy classes of subgroups $H \subset \Gamma $ such that $\Gamma/H $ is finite. But these are exactly the modular dessins d’enfants introduced by Grothendieck as I explained a while back elsewhere (see for example this post and others in the same series).
Comments closed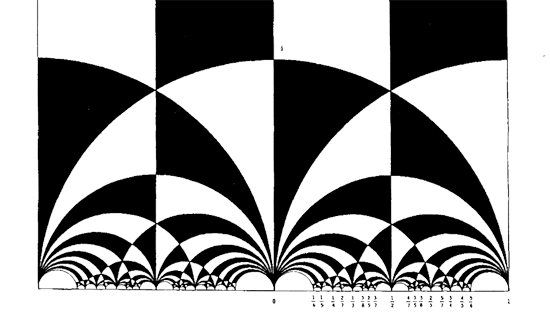 The black&white psychedelic picture on the left of a tessellation of the hyperbolic upper-halfplane, was called the Dedekind tessellation in
The black&white psychedelic picture on the left of a tessellation of the hyperbolic upper-halfplane, was called the Dedekind tessellation in  Stillwell refers to
Stillwell refers to