(After-math of last week’s second year lecture on elliptic
curves.)
We all know the story of Ramanujan and the taxicab, immortalized by Hardy
“I remember once going to see him when he was lying ill at Putney. I had ridden in taxicab no. 1729 and remarked that the number seemed to me rather a dull one, and that I hoped it was not an unfavorable omen. ‘No,’ he replied, ‘it’s a very interesting number; it is the smallest number expressible as a sum of two cubes in two different ways’.”
When I was ten, I wanted to become an archeologist and even today I can get pretty worked-up about historical facts. So, when I was re-telling this story last week I just had to find out things like :
the type of taxicab and how numbers were displayed on them and, related to this, exactly when and where did this happen, etc. etc. Half an hour free-surfing further I know a bit more than I wanted.
Let’s start with the date of this taxicab-ride, even the year changes from source to source, from 1917 in the dullness of 1729 (arguing that Hardy could never have made this claim as 1729 is among other things the third Carmichael Number, i.e., a pseudoprime relative to EVERY base) to ‘late in WW-1’ here…
Between 1917 and his return to India on march 13th 1919, Ramanujan was in and out a number of hospitals and nursing homes. Here’s an attempt to summarize these dates&places (based on the excellent paper Ramanujan’s Illness by D.A.B. Young).
(may 1917 -september 20th 1917) : Nursing Hostel, Thompson’s Lane in Cambridge.
(first 2 a 3 weeks of october 1917) : Mendip Hills Senatorium, near Wells in Somerset. (november 1917) : Matlock House Senatorium atMatlock in Derbyshire.
(june 1918 – november 1918) : Fitzroy House, a hospital in Fitzroy square in central London. (december 1918 – march 1919) : Colinette House, a private nursing home in Putney, south-west London. So, “he was lying ill at Putney” must have meant that Ramanujan was at Colinette House which was located 2, Colinette Road and a quick look with Google Earth

shows that the The British Society for the History of Mathematics Gazetteer is correct in asserting that “The house is no longer used as a nursing home and its name has vanished” as well as.”
“It was in 1919 (possibly January), when Hardy made the famous visit in the taxicab numbered 1729.”
Hence, we are looking for a London-cab early 1919. Fortunately, the London Vintage Taxi Association has a website including a taxi history page.
“At the outbreak of the First World War there was just one make available to buy, the Unic. The First World War devastated the taxi trade.
Production of the Unic ceased for the duration as the company turned to producing munitions. The majority of younger cabmen were called up to fight and those that remained had to drive worn-out cabs.
By 1918 these remnant vehicles were sold at highly inflated prices, often beyond the pockets of the returning servicemen, and the trade deteriorated.”
As the first post-war taxicab type was introduced in 1919 (which became known as the ‘Rolls-Royce of cabs’) more than likely the taxicab Hardy took was a Unic,

and the number 1729 was not a taxicab-number but part of its license plate. I still dont know whether there actually was a 1729-taxicab around at the time, but let us return to mathematics.
Clearly, my purpose to re-tell the story in class was to illustrate the use of addition on an elliptic curve as a mean to construct more rational solutions to the equation $x^3+y^3 = 1729 $ starting from the Ramanujan-points (the two solutions he was referring to) : P=(1,12) and Q=(9,10). Because the symmetry between x and y, the (real part of) curve looks like
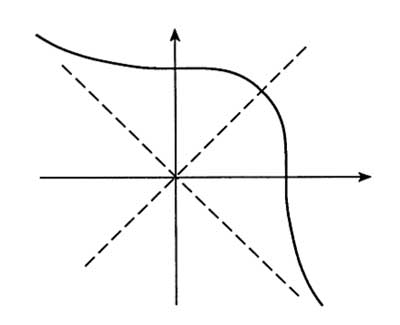
and if we take 0 to be the point at infinity corresponding to the asymptotic line, the negative of a point is just reflexion along the main diagonal. The geometric picture of addition of points on the curve is then summarized
in
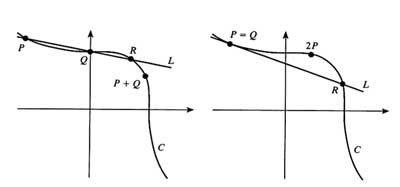
and sure enough we found the points $P+Q=(\frac{453}{26},-\frac{397}{26})$ and $(\frac{2472830}{187953},-\frac{1538423}{187953}) $ and so on by hand, but afterwards I had the nagging feeling that a lot more could have been said about this example. Oh, if Im allowed another historical side remark :
I learned of this example from the excellent book by Alf Van der Poorten Notes on Fermat’s last theorem page 56-57.
Alf acknowledges that he borrowed this material from a lecture by Frits Beukers ‘Oefeningen rond Fermat’ at the National Fermat Day in Utrecht, November 6th 1993.
Perhaps a more accurate reference might be the paper Taxicabs and sums of two cubes by Joseph Silverman which appeared in the april 1993 issue of The American Mathematical Monthly.
The above drawings and some material to follow is taken from that paper (which I didnt know last week). I could have proved that the Ramanujan points (and their reflexions) are the ONLY integer points on $x^3+y^3=1729 $.
In fact, Silverman gives a nice argument that there can only be finitely many integer points on any curve $x^3+y^3=A $ with $A \in \mathbb{Z} $ using the decomposition $x^3+y^3=(x+y)(x^2-xy+y^2) $.
So, take any factorization A=B.C and let $B=x+y $ and $C=x^2-xy+y^2 $, then substituting $y=B-x $ in the second one obtains that x must be an integer solution to the equation $3x^2-3Bx+(B^2-C)=0 $.
Hence, any of the finite number of factorizations of A gives at most two x-values (each giving one y-value). Checking this for A=1729=7.13.19 one observes that the only possibilities giving a square discriminant of the quadratic equation are those where $B=13, C=133 $ and $B=19, C=91 $ leading exactly to the Ramanujan points and their reflexions!
Sure, I mentioned in class the Mordell-Weil theorem stating that the group of rational solutions of an elliptic curve is always finitely generated, but wouldnt it be fun to determine the actual group in this example?
Surely, someone must have worked this out. Indeed, I did find a posting to sci.math.numberthy by Robert L. Ward : (in fact, there is a nice page on elliptic curves made from clippings to this newsgroup).
The Mordell-Weil group of the taxicab-curve is isomorphic to $\mathbb{Z} \oplus \mathbb{Z} $ and the only difference with Robert Wards posting was that I found besides his generator
$P=(273,409) $ (corresponding to the Ramanujan point (9,10)) as a second generator the point
$Q=(1729,71753) $ (note again the appearance of 1729…) corresponding to the rational solution $( -\frac{37}{3},\frac{46}{3}) $ on the taxicab-curve.
Clearly, there are several sets of generators (in fact that’s what $GL_2(\mathbb{Z}) $ is all about) and as our first generators were the same all I needed to see was that the point corresponding to the second Ramanujan point (399,6583) was of the form $\pm Q + a P $ for some integer a. Points and their addition is also easy to do with sage :
sage: P=T([273,409])
sage: Q=T([1729,71753])
sage: -P-Q
(399 : 6583 : 1)
and we see that the second Ramanujan point is indeed of the required form!
Leave a Comment
 give us all solutions
give us all solutions  The fact that there is one loop in each point, tells us that
The fact that there is one loop in each point, tells us that