geometry – Page 28 – neverendingbooks

Shameless Self-Promotion

Published July 18, 2007 by lieven

It looks like I’m off the hook and can relax (after a few months of rewriting/correcting/learning LaTeX-quirks). To all of you NeverEndingBooks readers : the bookproject has ended and will appear sometime this fall. It will be around 600 pages thick and cost just under 100$. This is about 4 times the amount NeverEndingBook-ers paid over at Lulu.com. To all (?!) those who did : treasure the two volumes, they will become (extremely rare) collectors’ items, one fine day. Here is the final cover-design :

Compare it to the covers produced two years ago by the NeverEndingBooks-design department (thanks again Jan and the rest of the crew).

The final fight was over the promotional material. The copywriters did include the captivating sentence “A Novel Approach to Difficult Cases in Mathematics and Physics”… Here’s my reply

I realize Im a difficult (some say hopeless) case, but there is little point advertising this. Here a few alternatives that may require spicing-up

“A gentle introduction to one of mathematics’ (and even physics’) hottest topics”
“A novel approach to noncommutative geometry”
“Get rid of singularities by going noncommutative!”
“The first readable text on an over-hyped topic…”
etc. etc.

I can do better if I have to, so please tell me and I’ll open up a bottle of wine.
Whatever you do, please remove the difficult cases-sentence from all material.

atb+apologies :: lieven.

UPDATE (august 1st) : if you want to order the book for your university-library, have a look at the promo flyer. All my suggestions (apart from the last one) are included…

One final comment about all of this. The project started as a bookproject with the AMS in 1999 and was abandoned (for a variety of reasons, all of them only relevant to myself) sometime early 2002.

Here’s the one thing that will hurt for some time to come. I wanted to dedicate the book to “the women in my life : my mother, Ann, Gitte&Bente”. Unfortunately, my mother will never see the book. The current dedication is :

This book is dedicated to the women in my life
Simonne Stevens (1926-2004), Ann, Gitte&Bente

Mathieu’s blackjack (3)

Published July 17, 2007 by lieven

If you only tune in now, you might want to have a look at the definition of Mathieu’s blackjack and the first part of the proof of the Conway-Ryba winning strategy involving the Steiner system S(5,6,12) and the Mathieu sporadic group $M_{12} $.

We’re trying to disprove the existence of misfits, that is, of non-hexad positions having a total value of at least 21 such that every move to a hexad would increase the total value. So far, we succeeded in showing that such a misfit must have the patern

$\begin{array}{|c|ccc|} \hline 6 & III & \ast & 9 \\ 5 & II & 7 & . \\ IV & I & 8 & . \\ \hline & & & \end{array} $

That is, a misfit must contain the 0-card (queen) and cannot contain the 10 or 11(jack) and must contain 3 of the four Romans. Now we will see that a misfit also contains precisely one of {5,6} (and consequently also exactly one card from {7,8,9}). To start, it is clear that it cannot contain BOTH 5 and 6 (then its total value can be at most 20). So we have to disprove that a misfit can miss {5,6} entirely (and so the two remaining cards (apart from the zero and the three Romans) must all belong to {7,8,9}).

Lets assume the misfit misses 5 and 6 and does not contain 9. Then, it must contain 4 (otherwise, its column-distribution would be (0,3,3,0) and it would be a hexad). There are just three such positions possible

$\begin{array}{|c|ccc|} \hline . & \ast & \ast & . \\ . & \ast & \ast & . \\ \ast & . & \ast & . \\ \hline – & – & ? & ? \end{array} $ $\begin{array}{|c|ccc|} \hline . & \ast & \ast & . \\ . & . & \ast & . \\ \ast & \ast & \ast & . \\ \hline – & + & ? & ? \end{array} $ $\begin{array}{|c|ccc|} \hline . & . & \ast & . \\ . & \ast & \ast & . \\ \ast & \ast & \ast & . \\ \hline – & 0 & ? & ? \end{array} $

Neither of these can be misfits though. In the first one, there is an 8->5 move to a hexad of smaller total value (in the second a 7->5 move and in the third a 7->6 move). Right, so the 9 card must belong to a misfit. Assume it does not contain the 4-card, then part of the misfit looks like (with either a 7- or an 8-card added)

$\begin{array}{|c|ccc|} \hline . & \ast & \ast & \ast \\ . & \ast & ? & . \\ . & \ast & ? & . \\ \hline & & & \end{array} $ contained in the unique hexad $\begin{array}{|c|ccc|} \hline \ast & \ast & \ast & \ast \\ . & \ast & & . \\ . & \ast & & . \\ \hline & & & \end{array} $

Either way the moves 7->6 or 8->6 decrease the total value, so it cannot be a misfit. Therefore, a misfit must contain both the 4- and 9-card. So it is of the form on the left below

$\begin{array}{|c|ccc|} \hline . & ? & \ast & \ast \\ . & ? & ? & . \\ \ast & ? & ? & . \\ \hline & & & \end{array} $ $\begin{array}{|c|ccc|} \hline . & . & \ast & . \\ . & \ast & \ast & \ast \\ \ast & \ast & . & . \\ \hline – & 0 & – & + \end{array} $ $\begin{array}{|c|ccc|} \hline . & . & \ast & \ast \\ . & \ast & \ast & . \\ \ast & \ast & . & . \\ \hline & & & \end{array} $

If this is a genuine misfit only the move 9->10 to a hexad is possible (the move 9->11 is not possible as all BUT ONE of {0,1,2,3,4} is contained in the misfit). Now, the only hexad containing 0,4,10 and 2 from {1,2,3} is in the middle, giving us what the misfit must look like before the move, on the right. Finally, this cannot be a misfit as the move 7->5 decreases the total value.

That is, we have proved the claim that a misfit must contain one of {5,6} and one of {7,8,9}. Right, now we can deliver the elegant finishing line of the Kahane-Ryba proof. A misfit must contain 0 and three among {1,2,3,4} (let us call the missing card s), one of $5+\epsilon $ with $0 \leq \epsilon \leq 1 $ and one of $7+\delta $ with $0 \leq \delta \leq 2 $. Then, the total value of the misfit is

$~(0+1+2+3+4-s)+(5+\epsilon)+(7+\delta)=21+(1+\delta+\epsilon-s) $

So, if this value is strictly greater than 21 (and we will see in a moment is has to be if it is at least 21) then we deduce that $s < 1 + \delta + \epsilon \leq 4 $. Therefore $1+\delta+\epsilon $ belongs to the misfit. But then the move $1+\delta \epsilon \rightarrow s $ moves the misfit to a 6-tuple with total value 21 and hence (as we see in a moment) must be a hexad and hence this is a decreasing move! So, finally, there are no misfits!

Hence, from every non-hexad pile of total value at least 21 we have a legal move to a hexad. Because the other player cannot move from an hexad to another hexad we are done with our strategy provided we can show (a) that the total value of any hexad is at least 21 and (b) that ALL 6-piles of total value 21 are hexads. As there are only 132 hexads it is easy enough to have their sum-distribution. Here it is

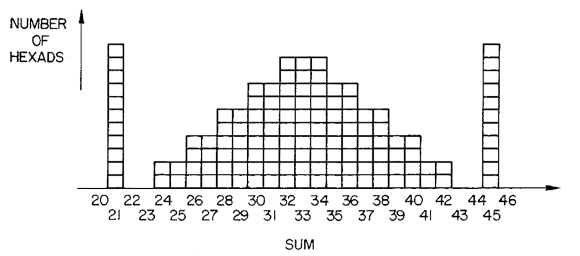
That is, (a) is proved by inspection and we see that there are 11 hexads of sum 21 (the light hexads in Conway-speak) and there are only 11 ways to get 21 as a sum of 6 distinct numbers from {0,1,..,11} so (b) follows. Btw. the obvious symmetry of the sum-distribution is another consequence of the duality t->11-t discussed briefly at the end of part 2.

Clearly, I’d rather have conceptual proofs for all these facts and briefly tried my hand. Luckily I did spot the following phrase on page 326 of Conway-Sloane (discussing the above distribution) :

“It will not be easy to explain all the above observations. They are certainly connected with hyperbolic geometry and with the ‘hole’ structure of the Leech lattice.”

So, I’d better leave it at this…

References

Joseph Kahane and Alexander J. Ryba, “The hexad game“

John H. Conway and N. J.A. Sloane, “Sphere packings, Lattices and Groups” chp. 11 ‘The Golay codes and the Mathieu groups’

Hexagonal Moonshine (3)

Published July 13, 2007 by lieven

Hexagons keep on popping up in the representation theory of the modular group and its close associates. We have seen before that singularities in 2-dimensional representation varieties of the three string braid group $B_3 $ are ‘clanned together’ in hexagons and last time Ive mentioned (in passing) that the representation theory of the modular group is controlled by the double quiver of the extended Dynkin diagram $\tilde{A_5} $, which is an hexagon…

Today we’re off to find representations of the extended modular group $\tilde{\Gamma} = PGL_2(\mathbb{Z}) $, which is obtained by adding to the modular group (see this post for a proof of generation)

$\Gamma = \langle U=\begin{bmatrix} 0 & -1 \\\ 1 & 0 \end{bmatrix},V=\begin{bmatrix} 0 & 1 \\\ -1 & 1 \end{bmatrix} \rangle $ the matrix $R=\begin{bmatrix} 0 & 1 \\\ 1 & 0 \end{bmatrix} $

In terms of generators and relations, one easily verfifies that

$\tilde{\Gamma} = \langle~U,V,R~|~U^2=R^2=V^3=(RU)^2=(RV)^2=1~\rangle $

and therefore $\tilde{\Gamma} $ is the amalgamated free product of the dihedral groups $D_2 $ and $D_3 $ over their common subgroup $C_2 = \langle~R~\rangle $, that is

$\tilde{\Gamma} = \langle U,R | U^2=R^2=(RU)^2=1 \rangle \ast_{\langle R | R^2=1 \rangle} \langle V,R | V^3=R^2=(RV)^2=1 \rangle = D_2 \ast_{C_2} D_3 $

From this description it is easy to find all n-dimensional $\tilde{\Gamma} $-representations $V $ and relate them to quiver-representations. $D_2 = C_2 \times C_2 $ and hence has 4 1-dimensonal simples $S_1,S_2,S_3,S_4 $. Restricting $V\downarrow_{D_2} $ to the subgroup $D_2 $ it decomposes as

$V \downarrow_{D_2} \simeq S_1^{\oplus a_1} \oplus S_2^{\oplus a_2} \oplus S_3^{\oplus a_3} \oplus S_4^{\oplus a_4} $ with $a_1+a_2+a_3+a_4=n $

Similarly, because $D_3=S_3 $ has two one-dimensional representations $T,S $ (the trivial and the sign representation) and one simple 2-dimensional representation $W $, restricting $V $ to this subgroup gives a decomposition

$V \downarrow_{D_3} \simeq T^{b_1} \oplus S^{\oplus b_2} \oplus W^{\oplus b_3} $, this time with $b_1+b_2+2b_3=n $

Restricting both decompositions further down to the common subgroup $C_2 $ one obtains a $C_2 $-isomorphism $V \downarrow_{D_2} \rightarrow^{\phi} V \downarrow_{D_3} $ which implies also that the above numbers must be chosen such that $a_1+a_3=b_1+b_3 $ and $a_2+a_4=b_2+b_3 $. We can summarize all this info about $V $ in a representation of the quiver

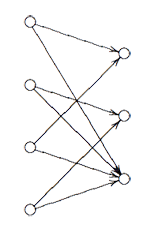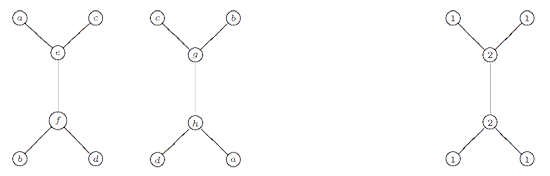
Here, the vertex spaces on the left are the iso-typical factors of $V \downarrow_{D_2} $ and those on the right those of $V \downarrow_{D_3} $ and the arrows give the block-components of the $C_2 $-isomorphism $\phi $. The nice things is that one can also reverse this process to get all $\tilde{\Gamma} $-representations from $\theta $-semistable representations of this quiver (having the additional condition that the square matrix made of the arrows is invertible) and isomorphisms of group-representation correspond to those of quiver-representations!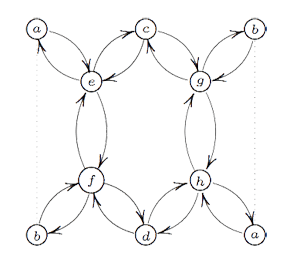

This proves that for all n the varieties of n-dimensional representations $\mathbf{rep}_n~\tilde{\Gamma} $ are smooth (but have several components corresponding to the different dimension vectors $~(a_1,a_2,a_3,a_4;b_1,b_2,b_3) $ such that $\sum a_i = n = b_1+b_2+2b_3 $.

The basic principle of _M-geometry_ is that a lot of the representation theory follows from the ‘clan’ (see this post) determined by the simples of smallest dimensions. In the case of the extended modular group $\tilde{\Gamma} $ it follows that there are exactly 4 one-dimensional simples and exactly 4 2-dimensional simples, corresponding to the dimension vectors

$\begin{cases} a=(0,0,0,1;0,1,0) \\\ b=(0,1,0,0;0,1,0) \\\ c=(1,0,0,0;1,0,0) \\\ d=(0,0,1,0;1,0,0) \end{cases} $ resp. $\begin{cases} e=(0,1,1,0;0,0,1) \\\ f=(1,0,0,1;0,0,1) \\\ g=(0,0,1,1;0,0,1) \\\ h=(1,1,0,0;0,0,1) \end{cases} $

If one calculates the ‘clan’ of these 8 simples one obtains the double quiver of the graph on the left. Note that a and b appear twice, so one should glue the left and right hand sides together as a Moebius-strip. That is, the clan determining the representation theory of the extended modular group is a Moebius strip made of two hexagons!

However, one should not focuss too much on the hexagons (that is, the extended Dynkin diagram $\tilde{A_5} $) here. The two ‘backbones’ (e–f and g–h) have their vertices corresponding to 2-dimensional simples whereas the topand bottom vertices correspond to one-dimensional simples. Hence, the correct way to look at this clan is as two copies of the double quiver of the extended Dynkin diagram $\tilde{D_5} $ glued over their leaf vertices to form a Moebius strip. Remark that the components of the sotropic root of $\tilde{D_5} $ give the dimensions of the corresponding $\tilde{\Gamma} $ simples.

The remarkable ubiquity of (extended) Dynkins never ceases to amaze!

Tag: geometry

Shameless Self-Promotion

Mathieu’s blackjack (3)

Hexagonal Moonshine (3)