Elkies – neverendingbooks

Surreal numbers & chess

Published April 8, 2008 by lieven

Most chess programs are able to give a numerical evaluation of a position. For example, the position below is considered to be worth +8.7 with white to move, and, -0.7 with black to move (by a certain program). But, if one applies combinatorial game theory as in John Conway’s ONAG and the Berlekamp-Conway-Guy masterpiece Winning Ways for your Mathematical Plays it will turn out that the position can be proved to have an infinitesimal advantage for white…

So, what do we mean by this? First some basic rules of combinatorial game theory. To start, we evaluate a position without knowing which player has the move. A zero-game is by definition a position in which neither player has a good move, that is, any move by either player quickly leads to losing the game. Hence, a zero-game is a position in which the second player to move wins.

What is the chess-equivalent of a zero-position game? A position in which neither player has a good move is called a Mutual Zugzwang in chess literature. An example is given by the above position, if we restrict attention only to the 4 pieces in the upper right-hand corner and forget the rest. We don’t know who has the move, but, White cannot move at all and Black cannot move the King or Bishop without losing the Bishop and allowing White to promote the pawn and win quickly. In CGT-parlance, the upper-right position has value $\{ \emptyset | \emptyset \} = 0 $ where the left options denote the White moves and the right options the Black moves.

All other values are determined by recursion. For example, consider a position in which White has just one move left before the sitution is again a Mutual Zugzwang, and, Black has no good move whatsoever. After white’s move, the position will again be a zero-position and Black has no options, so the value of this position would be denoted by $\{ 0 | \emptyset \} $ and we call the value of this position to be $+1 $. Similarly, if white has no options and black has one final move to make, the position would be considered to have value $\{ \emptyset | 0 \}= -1 $.

Clearly, these are just the three easiest game-values to have and the real kick comes further down the road when one can prove by recursion that some games have non-integer values (such as $\{ 0 | 1 \} = \frac{1}{2} $ for a position in which white has one move to get to a mutual zugzwang and black has a move leading to a position of value $+1 $ (defined as before)), or non-number values such as $\ast = \{ 0 | 0 \} $ where both white and black’s best move is to get to a mutal zugzwang. Game-values such as $\ast $ are called fuzzy (or confused with zero) and are defined by the property that the first player to move wins.

Similarly, positive game-values are those positions where White wins, independent of who has the move and negatives are those that Black wins. There is a whole menagery of game-values and the WinningWays-booklets give an example based introduction to this fascinating theory.

Brief as this introduction was, it will allow us to determine the exact value of the position in the above diagram. We know already that we can forget about the right-hand upper corner (as this is a zero-position) and concentrate attention to the left-hand side of the board.

It is easy to see that neither Knight can move without loosing quickly, nor can the pawns on a5 and b7. That is, white has just 2 options : either c3-c4 (quickly loosing after d5xc4 2. d3xc4,d4-d3 3. Nc1xd3,Na1-b3) or, and this is the only valid option c3xd4 leading to the position on the left below. Black has only one valid move : d4xc3 leading to the position on the right below.

Clearly, the left-diagram has value 0 as it is a mutual Zugzwang. The position on the right takes a moment’s thought : White has one move left d3-d4 leading to a 0-position, whereas black has one move d5-d4 leading to a position of value -1 (as black still has one move left d6-d5, whereas white has none). That is, the CGT-value of the right-hand position is $\{ 0 | -1 \} $ and therefore, the value of the starting position is precisely equal to

\[ \{ 0 | \{ 0 | -1 \} \} = +_{1} \]

(called tiny-one among ONAGers)

It can be shown that $+_1 $ has a positive value (that is, White wins independently of who has the first move) but smaller than any positive number-valued games!

Noam Elkies has written a beautiful paper On numbers and endgames: Combinatorial game theory in chess endgames containing many interesting examples (the example above is an adaptation of his diagram9).

The M(13)-groupoid (2)

Published July 30, 2007 by lieven

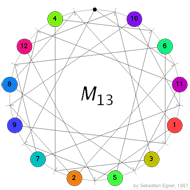Conway’s puzzle M(13) involves the 13 points and 13 lines of $\mathbb{P}^2(\mathbb{F}_3) $. On all but one point numbered counters are placed holding the numbers 1,…,12 and a move involves interchanging one counter and the ‘hole’ (the unique point having no counter) and interchanging the counters on the two other points of the line determined by the first two points. In the picture on the left, the lines are respresented by dashes around the circle in between two counters and the points lying on this line are those that connect to the dash either via a direct line or directly via the circle. In the first part we saw that the group of all reachable positions in Conway’s M(13) puzzle having the hole at the top positions contains the sporadic simple Mathieu group $M_{12} $ as a subgroup. To see the reverse inclusion we have to recall the definition of the ternary Golay code named in honour of the Swiss engineer Marcel Golay who discovered in 1949 the binary Golay code that we will encounter _later on_.

The ternary Golay code $\mathcal{C}_{12} $ is a six-dimenional subspace in $\mathbb{F}_3^{\oplus 12} $ and is spanned by its codewords of weight six (the Hamming distance of $\mathcal{C}_{12} $ whence it is a two-error correcting code). There are $264 = 2 \times 132 $ weight six codewords and they can be obtained from the 132 hexads, we encountered before as the winning positions of Mathieu’s blackjack, by replacing the stars by signs + or – using the following rules. By a tet (from tetracodeword) we mean a 3×4 array having 4 +-signs indicating the row-positions of a tetracodeword. For example

$~\begin{array}{|c|ccc|} \hline & + & & \\ + & & + & \\ & & & + \\ \hline + & 0 & + & – \end{array} $ is the tet corresponding to the bottom-tetracodeword. $\begin{array}{|c|ccc|} \hline & + & & \\ & + & & \\ & + & & \\ \hline & & & \end{array} $ A col is an array having +-signs along one of the four columns. The signed hexads will now be the hexads that can be written as $\mathbb{F}_3 $ vectors as (depending on the column-distributions of the stars in the hexad indicated between brackets)

$col-col~(3^20^2)\qquad \pm(col+tet)~(31^3) \qquad tet-tet~(2^30) \qquad \pm(col+col-tet)~(2^21^2) $

For example, the hexad on the right has column-distribution $2^30 $ so its signed versions are of the form tet-tet. The two tetracodewords must have the same digit (-) at place four (so that they cancel and leave an empty column). It is then easy to determine these two tetracodewords giving the signed hexad (together with its negative, obtained by replacing the order of the two codewords)

$\begin{array}{|c|ccc|} \hline \ast & \ast & & \\ \ast & & \ast & \\ & \ast & \ast & \\ \hline – & + & 0 & – \end{array} $ signed as
$\begin{array}{|c|ccc|} \hline + & & & \\ & & & \\ & + & + & + \\ \hline 0 & – & – & – \end{array} – \begin{array}{|c|ccc|} \hline & + & & \\ + & & + & \\ & & & + \\ \hline + & 0 & + & – \end{array} = \begin{array}{|c|ccc|} \hline + & – & & \\ – & & – & \\ & + & + & \\ \hline – & + & 0 & – \end{array} $

and similarly for the other cases. As Conway&Sloane remark ‘This is one of many cases when the process is easier performed than described’.

We have an order two operation mapping a signed hexad to its negative and as these codewords span the Golay code, this determines an order two automorphism of $\mathcal{C}_{12} $. Further, forgetting about signs, we get the Steiner-system S(5,6,12) of hexads for which the automorphism group is $M_{12} $ hence the automorphism group op the ternary Golay code is $2.M_{12} $, the unique nonsplit central extension of $M_{12} $.

Right, but what is the connection between the Golay code and Conway’s M(13)-puzzle which is played with points and lines in the projective plane $\mathbb{P}^2(\mathbb{F}_3) $? There are 13 points $\mathcal{P} $ so let us consider a 13-dimensional vectorspace $X=\mathbb{F}_3^{\oplus 13} $ with basis $x_p~:~p \in \mathcal{P} $. That is a vector in X is of the form $\vec{v}=\sum_p v_px_p $ and consider the ‘usual’ scalar product $\vec{v}.\vec{w} = \sum_p v_pw_p $ on X. Next, we bring in the lines in $\mathbb{P}^2(\mathbb{F}_3) $.

For each of the 13 lines l consider the vector $\vec{l} = \sum_{p \in l} x_p $ with support the four points lying on l and let $\mathcal{C} $ be the subspace (code) of X spanned by the thirteen vectors $\vec{l} $. Vectors $\vec{c},\vec{d} \in \mathcal{C} $ satisfy the remarkable identity $\vec{c}.\vec{d} = (\sum_p c_p)(\sum_p d_p) $. Indeed, both sides are bilinear in $\vec{c},\vec{d} $ so it suffices to check teh identity for two line-vectors $\vec{l},\vec{m} $. The right hand side is then 4.4=16=1 mod 3 which equals the left hand side as two lines either intersect in one point or are equal (and hence have 4 points in common). The identity applied to $\vec{c}=\vec{d} $ gives us (note that the squares in $\mathbb{F}_3 $ are {0,1}) information about the weight (that is, the number of non-zero digits) of codewords in $\mathcal{C} $

$wt(\vec{c})~mod(3) = \sum_p c_p^2 = (\sum_p c_p)^2 \in \{ 0,1 \} $

Let $\mathcal{C}’ $ be the collection of $\vec{c} \in \mathcal{C} $ of weight zero (modulo 3) then one can verify that $\mathcal{C}’ $ is the orthogonal complement of $\mathcal{C} $ with respect to the scalar product and that the dimension of $\mathcal{C} $ is seven whereas that of $\mathcal{C}’ $ is six.
Now, let for a point p be $\mathcal{G}_p $ the restriction of

$\mathcal{C}_p = \{ c \in \mathcal{C}~|~c_p = – \sum_{q \in \mathcal{P}} c_q \} $

to the coordinates of $\mathcal{P} – \{ p \} $, then $\mathcal{G}_p $ is clearly a six dimensional code in a 12-dimensional space. A bit more work shows that $\mathcal{G}_p $ is a self-dual code with minimal weight greater or equal to six, whence it must be the ternary Golay code! Now we are nearly done. _Next time_ we will introduce a reversi-version of M(13) and use the above facts to deduce that the basic group of the Mathieu-groupoid indeed is the sporadic simple group $M_{12} $.

References

Robert L. Griess, “Twelve sporadic groups” chp. 7 ‘The ternary Golay code and $2.M_{12} $’

John H. Conway and N. J.A. Sloane, “Sphere packings, lattices and groups” chp 11 ‘The Golay codes and the Mathieu groups’

John H. Conway, Noam D. Elkies and Jeremy L. Martin, ‘The Mathieu group $M_{12} $ and its pseudogroup extension $M_{13} $’ arXiv:math.GR/0508630

The Mathieu groupoid (1)

Published June 20, 2007 by lieven

Conway’s puzzle M(13) is a variation on the 15-puzzle played with the 13 points in the projective plane $\mathbb{P}^2(\mathbb{F}_3) $. The desired position is given on the left where all the counters are placed at at the points having that label (the point corresponding to the hole in the drawing has label 0). A typical move consists in choosing a line in the plane going through the point where the hole is, choose one of the three remaining points on this line and interchange the counter on it for the hole while at the same time interchanging the counters on the other two points. In the drawing on the left, lines correspond to the little-strokes on the circle and edges describe which points lie on which lines. For example, if we want to move counter 5 to the hole we notice that both of them lie on the line represented by the stroke just to the right of the hole and this line contains also the two points with counters 1 and 11, so we have to replace these two counters too in making a move. Today we will describe the groupoid corresponding to this slide-puzzle so if you want to read on, it is best to play a bit with Sebastian Egner’s M(13) Java Applet to see the puzzle in action (and to use it to verify the claims made below). Clicking on a counter performs the move taking the counter to the hole.

Tag: Elkies

Surreal numbers & chess

The M(13)-groupoid (2)

The Mathieu groupoid (1)