Conway and Norton showed that there are exactly 171 moonshine functions and associated two arithmetic subgroups to them. We want a tool to describe these and here’s where Conway’s big picture comes in very handy. All moonshine groups are arithmetic groups, that is, they are commensurable with the modular group. Conway’s idea is to view several of these groups as point- or set-wise stabilizer subgroups of finite sets of (projective) commensurable 2-dimensional lattices.
Expanding (and partially explaining) the original moonshine observation of McKay and Thompson, John Conway and Simon Norton formulated monstrous moonshine :
To every cyclic subgroup $\langle m \rangle $ of the Monster $\mathbb{M} $ is associated a function
$f_m(\tau)=\frac{1}{q}+a_1q+a_2q^2+\ldots $ with $q=e^{2 \pi i \tau} $ and all coefficients $a_i \in \mathbb{Z} $ are characters at $m $ of a representation of $\mathbb{M} $. These representations are the homogeneous components of the so called Moonshine module.
Each $f_m $ is a principal modulus for a certain genus zero congruence group commensurable with the modular group $\Gamma = PSL_2(\mathbb{Z}) $. These groups are called the moonshine groups.
Conway and Norton showed that there are exactly 171 different functions $f_m $ and associated two arithmetic subgroups $F(m) \subset E(m) \subset PSL_2(\mathbb{R}) $ to them (in most cases, but not all, these two groups coincide).
Whereas there is an extensive literature on subgroups of the modular group (see for instance the series of posts starting here), most moonshine groups are not contained in the modular group. So, we need a tool to describe them and here’s where Conway’s big picture comes in very handy.
All moonshine groups are arithmetic groups, that is, they are subgroups $G $ of $PSL_2(\mathbb{R}) $ which are commensurable with the modular group $\Gamma = PSL_2(\mathbb{Z}) $ meaning that the intersection $G \cap \Gamma $ is of finite index in both $G $ and in $\Gamma $. Conway’s idea is to view several of these groups as point- or set-wise stabilizer subgroups of finite sets of (projective) commensurable 2-dimensional lattices.
Start with a fixed two dimensional lattice $L_1 = \mathbb{Z} e_1 + \mathbb{Z} e_2 = \langle e_1,e_2 \rangle $ and we want to name all lattices of the form $L = \langle v_1= a e_1+ b e_2, v_2 = c e_1 + d e_2 \rangle $ that are commensurable to $L_1 $. Again this means that the intersection $L \cap L_1 $ is of finite index in both lattices. From this it follows immediately that all coefficients $a,b,c,d $ are rational numbers.
It simplifies matters enormously if we do not look at lattices individually but rather at projective equivalence classes, that is $~L=\langle v_1, v_2 \rangle \sim L’ = \langle v’_1,v’_2 \rangle $ if there is a rational number $\lambda \in \mathbb{Q} $ such that $~\lambda v_1 = v’_1, \lambda v_2=v’_2 $. Further, we are of course allowed to choose a different ‘basis’ for our lattices, that is, $~L = \langle v_1,v_2 \rangle = \langle w_1,w_2 \rangle $ whenever $~(w_1,w_2) = (v_1,v_2).\gamma $ for some $\gamma \in PSL_2(\mathbb{Z}) $.
Using both operations we can get any lattice in a specific form. For example,
$\langle \frac{1}{2}e_1+3e_2,e_1-\frac{1}{3}e_2 \overset{(1)}{=} \langle 3 e_1+18e_2,6e_1-2e_2 \rangle \overset{(2)}{=} \langle 3 e_1+18 e_2,38 e_2 \rangle \overset{(3)}{=} \langle \frac{3}{38}e_1+\frac{9}{19}e_2,e_2 \rangle $
Here, identities (1) and (3) follow from projective equivalence and identity (2) from a base-change. In general, any lattice $L $ commensurable to the standard lattice $L_1 $ can be rewritten uniquely as $L = \langle Me_1 + \frac{g}{h} e_2,e_2 \rangle $ where $M $ a positive rational number and with $0 \leq \frac{g}{h} < 1 $.
Another major feature is that one can define a symmetric hyper-distance between (equivalence classes of) such lattices. Take $L=\langle Me_1 + \frac{g}{h} e_2,e_2 \rangle $ and $L’=\langle N e_1 + \frac{i}{j} e_2,e_2 \rangle $ and consider the matrix
$D_{LL’} = \begin{bmatrix} M & \frac{g}{h} \\ 0 & 1 \end{bmatrix} \begin{bmatrix} N & \frac{i}{j} \\ 0 & 1 \end{bmatrix}^{-1} $ and let $\alpha $ be the smallest positive rational number such that all entries of the matrix $\alpha.D_{LL’} $ are integers, then
$\delta(L,L’) = det(\alpha.D_{LL’}) \in \mathbb{N} $ defines a symmetric hyperdistance which depends only of the equivalence classes of lattices (hyperdistance because the log of it behaves like an ordinary distance).
Conway’s big picture is the graph obtained by taking as its vertices the equivalence classes of lattices commensurable with $L_1 $ and with edges connecting any two lattices separated by a prime number hyperdistance. Here’s part of the 2-picture, that is, only depicting the edges of hyperdistance 2.
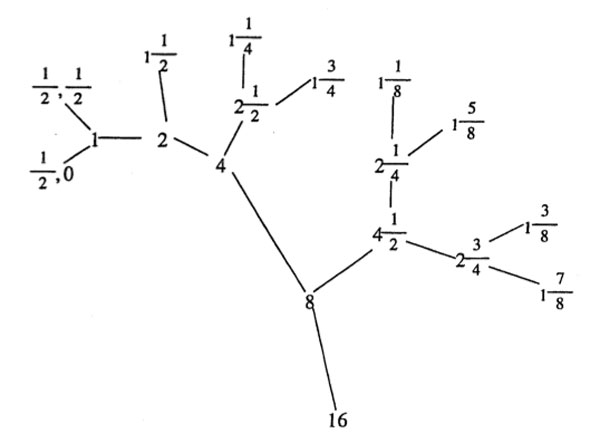
The 2-picture is an infinite 3-valent tree as there are precisely 3 classes of lattices at hyperdistance 2 from any lattice $L = \langle v_1,v_2 \rangle $ namely (the equivalence classes of) $\langle \frac{1}{2}v_1,v_2 \rangle~,~\langle v_1, \frac{1}{2} v_2 \rangle $ and $\langle \frac{1}{2}(v_1+v_2),v_2 \rangle $.
Similarly, for any prime hyperdistance p, the p-picture is an infinite p+1-valent tree and the big picture is the product over all these prime trees. That is, two lattices at square-free hyperdistance $N=p_1p_2\ldots p_k $ are two corners of a k-cell in the big picture!
(Astute readers of this blog (if such people exist…) may observe that Conway’s big picture did already appear here prominently, though in disguise. More on this another time).
The big picture presents a simple way to look at arithmetic groups and makes many facts about them visually immediate. For example, the point-stabilizer subgroup of $L_1 $ clearly is the modular group $PSL_2(\mathbb{Z}) $. The point-stabilizer of any other lattice is a certain conjugate of the modular group inside $PSL_2(\mathbb{R}) $. For example, the stabilizer subgroup of the lattice $L_N = \langle Ne_1,e_2 \rangle $ (at hyperdistance N from $L_1 $) is the subgroup
${ \begin{bmatrix} a & \frac{b}{N} \\ Nc & d \end{bmatrix}~|~\begin{bmatrix} a & b \\ c & d \end{bmatrix} \in PSL_2(\mathbb{Z})~} $
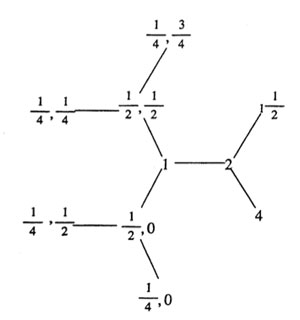Now the intersection of these two groups is the modular subgroup $\Gamma_0(N) $ (consisting of those modular group element whose lower left-hand entry is divisible by N). That is, the proper way to look at this arithmetic group is as the joint stabilizer of the two lattices $L_1,L_N $. The picture makes it trivial to compute the index of this subgroup.
Consider the ball $B(L_1,N) $ with center $L_1 $ and hyper-radius N (on the left, the ball with hyper-radius 4). Then, it is easy to show that the modular group acts transitively on the boundary lattices (including the lattice $L_N $), whence the index $[ \Gamma : \Gamma_0(N)] $ is just the number of these boundary lattices. For N=4 the picture shows that there are exactly 6 of them. In general, it follows from our knowledge of all the p-trees the number of all lattices at hyperdistance N from $L_1 $ is equal to $N \prod_{p | N}(1+ \frac{1}{p}) $, in accordance with the well-known index formula for these modular subgroups!
But, there are many other applications of the big picture giving a simple interpretation for the Hecke operators, an elegant proof of the Atkin-Lehner theorem on the normalizer of $\Gamma_0(N) $ (the whimsical source of appearances of the number 24) and of Helling’s theorem characterizing maximal arithmetical groups inside $PSL_2(\mathbb{C}) $ as conjugates of the normalizers of $\Gamma_0(N) $ for square-free N.
J.H. Conway’s paper “Understanding groups like $\Gamma_0(N) $” containing all this material is a must-read! Unfortunately, I do not know of an online version.
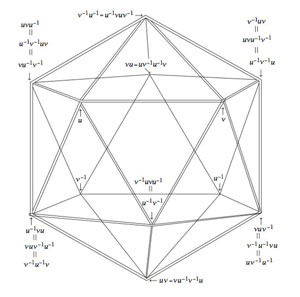The alternating group $A_5 $ has two conjugacy classes of order 5 elements, both consisting of exactly 12 elements. Fix one of these conjugacy classes, say $C $ and construct a graph with vertices the 12 elements of $C $ and an edge between two $u,v \in C $ if and only if the group-product $u.v \in C $ still belongs to the same conjugacy class.
The character table of $A_5 $ is given on the left : the five columns correspond to the different conjugacy classes of elements of order resp. 1,2,3,5 and 5 and the rows are the character functions of the 5 irreducible representations of dimensions 1,3,3,4 and 5.
There are exactly 2 conjugacy classes of involutions, usually denoted 2A and 2B. Involutions in class 2A are called “Fischer-involutions”, after 
As in the case of the icosahedral graph, the number of vertices and their common valency does not determine the monster graph uniquely. To gain more insight, we would like to know more about the sizes of minimal circuits in the graph, the number of such minimal circuits going through a fixed vertex, and so on.
We