Tag: braid group

In another post we introduced
Minkowski’s question-mark function, aka the devil’s straircase
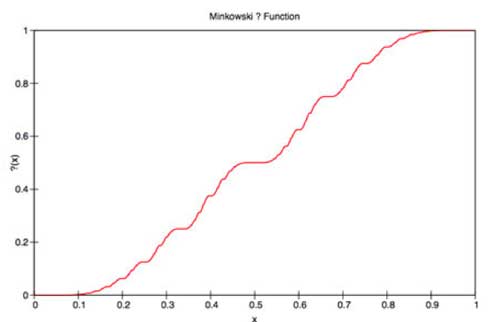and related it to
Conways game of _contorted fractions_. Side remark : over at Good Math, Bad Math Mark Chu-Carroll is running
a mini-series on numbers&games, so far there is a post on surreal numbers,
surreal arithmetic and the connection with
games but
probably this series will go on for some time.

About a year ago I had
an email-exchange with Linas Vepstas because I was
intrigued by one of his online publications linking the fractal
symmetries of the devil’s staircase to the modular group. Unfortunately,
his paper contained some inaccuracies and I’m happy some of my comments
made it into his rewrite The Minkowski question mark, GL(2,Z) and the
modular group. Still, several
mistakes remain so read this paper only modulo his own caveat

XXXX This paper is unfinished. Although this version
corrects a number of serious errors in the previous drafts, it is still
misleading and confusing in many ways. The second half, in particular
must surely contain errors and mis-statements! Caveat emptor! XXXX

For example, on page 15 of the march 24-version he claims
that the third braid group $B_3\simeq S{L}_2(\mathbb{Z})$ which
would make life, mathematics and even physics a lot easier, but
unfortunately is not true. Recall that Artin’s defining relation for the
3-string braid group is ${\sigma }_1{\sigma }_2{\sigma }_1={\sigma }_2{\sigma }_1{\sigma }_2$ as can be seen because the 3-strings below can
be transformed into each other
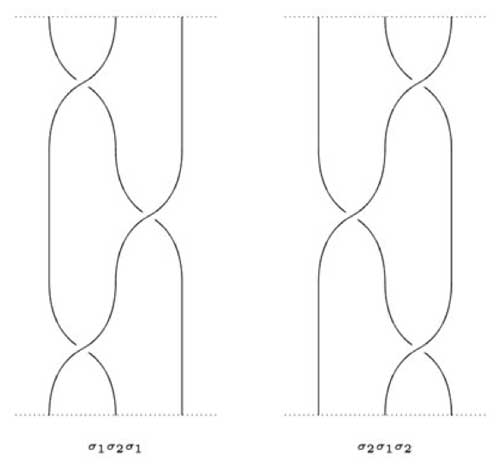But from this
relation it follows that $c=({\sigma }_1{\sigma }_2{\sigma }_1{)}^2$ is
a central element in $B_3$ and it is not difficult to verify
that indeed $B_3/⟨c⟩\simeq PS{L}_2(\mathbb{Z})$
and $B_3/⟨c^2⟩\simeq S{L}_2(\mathbb{Z})$ An easy
way to see that the third braid group and the modular group are quite
different is to look at their one-dimensional representations. Any
group-map $\text{Missing open brace for superscript}$ is determined by
non-zero complex numbers x and y satisfying $x^{2}y=y^{2}x$ so are
parametrized by the torus $\text{Missing open brace for superscript}$ whereas there are only
6 one-dimensional representations of $PS{L}_2(\mathbb{Z})=C_2\ast C_3$ (and similarly, there are only 12 one-dimensional
$S{L}_2(\mathbb{Z})$-representations). Btw. for those still
interested in noncommutative geometry : $(P)S{L}_2(\mathbb{Z})$
are noncommutative manifolds whereas $B_3$ is definitely
singular, if I ever get to the definitions of all of this… Still,
there is a gem contained in Linas’ paper and here’s my reading of it :
the fractal symmetries of the devil’s staircase form a generating
sub-semigroup $C_2\ast \mathbb{N}$ of
$G{L}_2(\mathbb{Z})$ . To begin, let us recall that the
question-mark function is defined in terms of continued fraction
expressions. So, what group of symmetries may be around the corner?
Well, if $a=⟨a_0;a_1,a_2,\dots ⟩$ is the
continued fraction of a (see this
post for details) then if we
look at the n-th approximations $\frac{p_n}{q_n}$ (that is, the
rational numbers obtained after breaking off the continued fraction at
step n) it is failrly easy to show that $\left[\begin{array}{cc}{p}_n& p_{n-1}\\ q_n& q_{n-1}\end{array}\right]\in G{L}_2(\mathbb{Z})$ and
recall (again) that this group acts on
${\mathbb{P}}_{\mathbb{C}}^1$ via Moebius transformations
$\left[\begin{array}{ccc}a& bc& d\end{array}\right]$ via $z\mapsto \frac{az+b}{cz+d}$ One of the symmetries is easy to spot
(reflexion along the 1/2-axis) 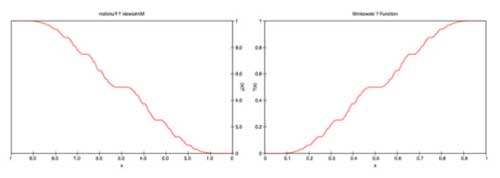That is, $?(x-1)=1–?(x)$ Observe that the left-hand
side transformation is given by the Moebius transformation determined by
the matrix $r=\left[\begin{array}{cc}-1& 1\\ 0& 1\end{array}\right]\in G{L}_2(\mathbb{Z})$ Other symmetries are harder to see as they are
_fractal symmetries_, that is they are self-symmetries but at different
scales. For example, let us blow-up the ?-function at the interval
[1/3,1/2] and compare it with the function at the interval [1/2,1]
which has the same graph, while halving the function value. More
generally, substituting the ?-function definition using continued
fraction expressions one verifies that $?(\frac{x}{x+1})=\frac{1}{2}?(x)$ and this time the left-hand transformation is
determined by the matrix $g=\left[\begin{array}{cc}1& 0\\ 1& 1\end{array}\right]\in G{L}_2(\mathbb{Z})$ We obtain a semi-group $S=⟨r,g⟩$ of fractal symmetries which are induced (the
right hand sides of the above expressions) via a 2-dimensional
representation of S $S\to G{L}_2(\mathbb{C})r\mapsto \left[\begin{array}{cc}1& 0\\ 1& -1\end{array}\right]g\mapsto \left[\begin{array}{cc}1& 0\\ 0& \frac{1}{2}\end{array}\right]$ acting
via left-multiplication on the two-dimensional vectorspace
$\mathbb{C}1+\mathbb{C}x$. We claim that S is the free
semi-group $C_2\ast \mathbb{N}$. Clearly, $r^2=1$ and
g is of infinite order, but we have to show that no expression of the
form $r{g}^{i_1}r{g}^{i_2}r\dots r{g}^{i_l}r$ can be the identity
in S. We will prove this by computing its action on the continued
fraction expression of $a=⟨0;a_0,a_1,\dots ⟩$.
It is a pleasant exercise to show that $g.⟨0;a_1,a_2,\dots ⟩=⟨0;a_1+1,a_2,\dots ⟩$ whence by induction
$g^n.⟨0;a_1,a_2,\dots ⟩=⟨0;a_1+n,a_2,\dots ⟩$ Moreover, the action on r is given by $r.⟨0;a_1,a_2,\dots ⟩=⟨0;1,a_1-1,a_2,\dots ⟩$ if
$a_1\ne 1$ whereas $r.⟨0;1,a_2,a_3,\dots ⟩=⟨0;a_2+1,a_3,\dots ⟩$ But then, as a
consequence we have that $g^{n-1}rg.⟨0;a_1,a_2,\dots ⟩=⟨0;n,a_1,a_2,\dots ⟩$ and iterating this
procedure gives us finally that an expression $g^{j-1}r{g}^{k}r{g}^{l}r\dots g^{z}rg=(g^{j-1}rg)(g^{k-1}rg)(g^{l-1}rg)\dots (g^{z-1}rg)$ acts on $a=⟨0;a_1,a_2,\dots ⟩$ by sending it to $⟨0;j,k,l,\dots ,z,a_1,a_2,\dots ⟩$ whence such an expression
can never act as the identity element, proving that indeed $S\simeq C_2\ast \mathbb{N}$. As for the second claim, recall from this
post that
$G{L}_2(\mathbb{Z})$ is generated by the matrices $U=\left[\begin{array}{ccc}0& -11& 0\end{array}\right]V=\left[\begin{array}{ccc}0& 1-1& 1\end{array}\right]R=\left[\begin{array}{ccc}0& 11& 0\end{array}\right]$ and a straightforward verification shows that
$r=RV,g=VU$ and $R=g^{-1}rg,V=g^{-1}rgr,U=r{g}^{-1}r{g}^2$ whence, indeed, the semi-group S
generates the whole of $G{L}_2(\mathbb{Z})$!