Tag: Baez

I was running a bachelor course on representations of finite groups and a master course on simple (mainly sporadic) groups until Corona closed us down. Perhaps these blog-posts can be useful to some.

A curious fact, with ripple effect on Mathieu sporadic groups, is that the symmetric group $S_6$ has an automorphism $\varphi$, different from an automorphism by conjugation.

In the course notes the standard approach was given, based on the $5$-Sylow subgroups of $S_5$.

Here’s the idea. Let $S_6$ act by permuting $6$ elements and consider the subgroup $S_5$ fixing say $6$. If such an odd automorphism $\varphi$ would exist, then the subgroup $\varphi (S_5)$ cannot fix one of the six elements (for then it would be conjugated to $S_5$), so it must act transitively on the six elements.

The alternating group $A_5$ is the rotation symmetry group of the icosahedron

Any $5$-Sylow subgroup of $A_5$ is the cyclic group $C_5$ generated by a rotation among one of the six body-diagonals of the icosahedron. As $A_5$ is normal in $S_5$, also $S_5$ has six $5$-Sylows.

More lowbrow, such a subgroup is generated by a permutation of the form $(1,2,a,b,c)$, of which there are six. Good old Sylow tells us that these $5$-Sylow subgroups are conjugated, giving a monomorphism
$$S_5\to Sym(\{5-Sylows\})\simeq S_6$$
and its image $H$ is a subgroup of $S_6$ of index $6$ (and isomorphic to $S_5$) which acts transitively on six elements.

Left multiplication gives an action of $S_6$ on the six cosets $S_6/H=\{\sigma H:\sigma \in S_6\}$, that is a groupmorphism
$$\varphi :S_6\to Sym(\{\sigma H\})=S_6$$
which is our odd automorphism (actually it is even, of order two). A calculation shows that $\varphi$ sends permutations of cycle shape ${2.1}^4$ to shape $2^3$, so can’t be given by conjugation (which preserves cycle shapes).

An alternative approach is given by Noah Snyder in an old post at the Secret Blogging Seminar.

Here, we like to identify the six points $\{a,b,c,d,e,f\}$ with the six points $\{0,1,2,3,4,\mathrm{\infty }\}$ of the projective line ${\mathbb{P}}^1({\mathbb{F}}_5)$ over the finite field ${\mathbb{F}}_5$.

There are $6!$ different ways to do this set-theoretically, but lots of them are the same up to an automorphism of ${\mathbb{P}}^1({\mathbb{F}}_5)$, that is an element of $PG{L}_2({\mathbb{F}}_5)$ acting via Mobius transformations on ${\mathbb{P}}^1({\mathbb{F}}_5)$.

$PG{L}_2({\mathbb{F}}_5)$ acts $3$-transitively on ${\mathbb{P}}^1({\mathbb{F}}_5)$ so we can fix three elements in each class, say $a=0,b=1$ and $f=\mathrm{\infty }$, leaving six different ways to label the points of the projective line
$$\begin{array}{ccccccc}& a& b& c& d& e& f\\ 1& 0& 1& 2& 3& 4& \mathrm{\infty }\\ 2& 0& 1& 2& 4& 3& \mathrm{\infty }\\ 3& 0& 1& 3& 2& 4& \mathrm{\infty }\\ 4& 0& 1& 3& 4& 2& \mathrm{\infty }\\ 5& 0& 1& 4& 2& 3& \mathrm{\infty }\\ 6& 0& 1& 4& 3& 2& \mathrm{\infty }\end{array}$$
A permutation of the six elements $\{a,b,c,d,e,f\}$ will result in a permutation of the six classes of ${\mathbb{P}}^1({\mathbb{F}}_5)$-labelings giving the odd automorphism
$$\varphi :S_6=Sym(\{a,b,c,d,e,f\})\to Sym(\{1,2,3,4,5,6\})=S_6$$
An example: the involution $(a,b)$ swaps the points $0$ and $1$ in ${\mathbb{P}}^1({\mathbb{F}}_5)$, which can be corrected via the Mobius-automorphism $t\mapsto 1-t$. But this automorphism has an effect on the remaining points
$$2\leftrightarrow 43\leftrightarrow 3\mathrm{\infty }\leftrightarrow \mathrm{\infty }$$
So the six different ${\mathbb{P}}^1({\mathbb{F}}_5)$ labelings are permuted as
$$\varphi ((a,b))=(1,6)(2,5)(3,4)$$
showing (again) that $\varphi$ is not a conjugation-automorphism.

Yet another, and in fact the original, approach by James Sylvester uses the strange terminology of duads, synthemes and synthematic totals.

• A duad is a $2$-element subset of $\{1,2,3,4,5,6\}$ (there are $15$ of them).
• A syntheme is a partition of $\{1,2,3,4,5,6\}$ into three duads (there are $15$ of them).
• A (synthematic) total is a partition of the $15$ duads into $5$ synthemes, and they are harder to count.

There’s a nice blog-post by Peter Cameron on this, as well as his paper From $M_{12}$ to $M_{24}$ (after Graham Higman). As my master-students have to work their own way through this paper I will not spoil their fun in trying to deduce that

• Two totals have exactly one syntheme in common, so synthemes are ‘duads of totals’.
• Three synthemes lying in disjoint pairs of totals must consist of synthemes containing a fixed duad, so duads are ‘synthemes of totals’.
• Duads come from disjoint synthemes of totals in this way if and only if they share a point, so points are ‘totals of totals’

My hint to the students was “Google for John Baez+six”, hoping they’ll discover Baez’ marvellous post Some thoughts on the number $6$, and in particular, the image (due to Greg Egan) in that post

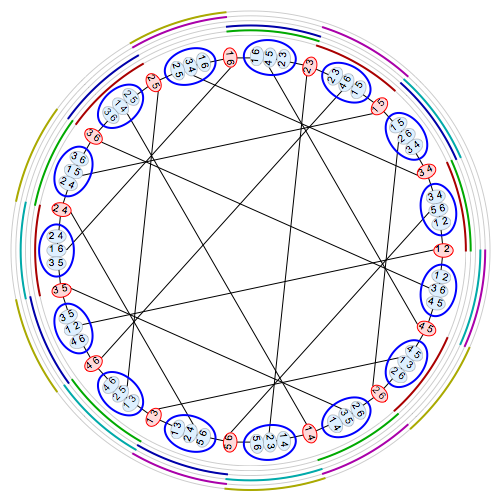
which makes everything visually clear.

The duads are the $15$ red vertices, the synthemes the $15$ blue vertices, connected by edges when a duad is contained in a syntheme. One obtains the Tutte-Coxeter graph.

The $6$ concentric rings around the picture are the $6$ synthematic totals. A band of color appears in one of these rings near some syntheme if that syntheme is part of that synthematic total.

If $\{t_1,t_2,t_3,t_4,t_5,t_6\}$ are the six totals, then any permutation $\sigma$ of $\{1,2,3,4,5,6\}$ induces a permutation $\varphi (\sigma )$ of the totals, giving the odd automorphism
$$\varphi :S_6=Sym(\{1,2,3,4,5,6\})\to Sym(\{t_1,t_2,t_3,t_4,t_5,t_6\})=S_6$$