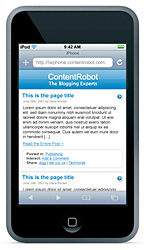
 If you have an iPhone or iPod Touch and point your Safari browser to this blog you can now view it in optimised format, thanks to the iWPhone WordPress Plugin and Theme. I’ve only changed the CSS slightly to have the same greeny look-and-feel of the current redoable theme.
If you have an iPhone or iPod Touch and point your Safari browser to this blog you can now view it in optimised format, thanks to the iWPhone WordPress Plugin and Theme. I’ve only changed the CSS slightly to have the same greeny look-and-feel of the current redoable theme.
Upgrading a WordPress-blog running under Tiger (Mac OS 10.4) to Leopard produces a few anxiety moments. All of the standard tools (Apache, PHP and MySQL) seem no longer to work as before. For those of you who do not want to waste too much time over it, I’ll walk through the process.
After upgrading to Leopard you want to check whether your blog is still alive, so you fire up Safari and will be greeted by the message that Safari cannot find your server. Sure enough you forgot to start the WebServer in SystemPreferences/Sharing/Web Sharing. Having fixed this you will see the default Apache-screen because Leopard put these default-files in your webserver-root directory (/Library/WebServer/Documents). In case you installed your blog under a user account you will get a message that you enter forbidden territory, see below for the solution to that problem. Having removed all those index.html files (making sure NOT to delete the index.php of your blog) a more serious problem presents itself : you see the text-version of index.php meaning that PHP isnt working. You check the /etc/httpd/httpd.conf file and it still contains all the changes you made to it to get PHP running under Tiger, so what is going on?
Googling for something like ‘enabling PHP under Leopard’ you’ll discover that the configuration file used by the webserver is in a different location. It now resides at /private/etc/apache2/httpd.conf. You will have to remove the hash sign (#) at the beginning of line 114 so that it reads
LoadModule php5_module libexec/apache2/libphp5.so
Next, you have to create a php.ini file and change one line. The first thing is settled by the following Terminal-commands
cd /private/etc
sudo cp php.ini.default php.ini
and in the php.ini you have to modify line 305 so that it becomes (removing the latter part of the line)
error_reporting = E_ALL
Restarting the webserver enables PHP. If you need more details check out the article Enabling PHP and Apache in Leopard. However, you are not quite done yet. Your blog will now show the WordPress-page that something is wrong with your mysql-database. However, mysql seems to be running fine as you can check from the Terminal so PHP cannot find it.
To remedy this, you have to add the locations (after the = sign) in the follwing two lines of the php.ini file
mysql.default_socket = /private/tmp/mysql.sock
mysqli.default_socket = /private/tmp/mysql.sock
Restarting the webserver should resolve the problem. But then your blog can still choke on old PHP-code in one of the plugins you use. In my case I was using an ancient version of the PHP-Markdown plugin but after replacing it with the newest version NeB looked just like I left it with Tiger…
A final point : webpages stored in personal Sites-folders cannot be served by Apache2 and will produce a message that you have not enough privileges to view the page. To resolve this, type the following command from the Terminal
sudo cp /private/etc/httpd/users/*.conf /private/etc/Apache2/users
Leave a Comment In 1773,
In 1773,  A PROBLEM
A PROBLEM