Quiver Grassmannians can be anything

A standard Grassmannian $Gr(m,V)$ is the manifold having as its points all possible $m$-dimensional subspaces of a given vectorspace $V$. As an example, $Gr(1,V)$ is the set of lines through the origin in $V$ and therefore is the projective space $\mathbb{P}(V)$. Grassmannians are among the nicest projective varieties, they are smooth and allow a cell decomposition.

A quiver $Q$ is just an oriented graph. Here’s an example

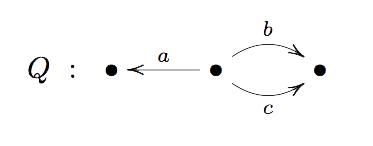
A representation $V$ of a quiver assigns a vector-space to each vertex and a linear map between these vertex-spaces to every arrow. As an example, a representation $V$ of the quiver $Q$ consists of a triple of vector-spaces $(V_1,V_2,V_3)$ together with linear maps $f_a:V_2\to V_1$ and $f_b,f_c:V_2\to V_3$.

A sub-representation $W\subset V$ consists of subspaces of the vertex-spaces of $V$ and linear maps between them compatible with the maps of $V$. The dimension-vector of $W$ is the vector with components the dimensions of the vertex-spaces of $W$.

This means in the example that we require $f_a(W_2)\subset W_1$ and $f_b(W_2)$ and $f_c(W_2)$ to be subspaces of $W_3$. If the dimension of $W_i$ is $m_i$ then $m=(m_1,m_2,m_3)$ is the dimension vector of $W$.

The quiver-analogon of the Grassmannian $Gr(m,V)$ is the Quiver Grassmannian $QGr(m,V)$ where $V$ is a quiver-representation and $QGr(m,V)$ is the collection of all possible sub-representations $W\subset V$ with fixed dimension-vector $m$. One might expect these quiver Grassmannians to be rather nice projective varieties.

However, last week Markus Reineke posted a 2-page note on the arXiv proving that every projective variety is a quiver Grassmannian.

Let’s illustrate the argument by finding a quiver Grassmannian $QGr(m,V)$ isomorphic to the elliptic curve in ${\mathbb{P}}^2$ with homogeneous equation $Y^{2}Z=X^3+Z^3$.

Consider the Veronese embedding ${\mathbb{P}}^2\to {\mathbb{P}}^9$ obtained by sending a point $(x:y:z)$ to the point

$$(x^3:x^{2}y:x^{2}z:x{y}^2:xyz:x{z}^2:y^3:y^{2}z:y{z}^2:z^3)$$

The upshot being that the elliptic curve is now realized as the intersection of the image of ${\mathbb{P}}^2$ with the hyper-plane $\mathbb{V}(X_0-X_7+X_9)$ in the standard projective coordinates $(x_0:x_1:\cdots :x_9)$ for ${\mathbb{P}}^9$.

To describe the equations of the image of ${\mathbb{P}}^2$ in ${\mathbb{P}}^9$ consider the $6\times 3$ matrix with the rows corresponding to $(x^2,xy,xz,y^2,yz,z^2)$ and the columns to $(x,y,z)$ and the entries being the multiplications, that is

$$\left[\begin{array}{ccc}{x}^3& x^{2}y& x^{2}z\\ x^{2}y& x{y}^2& xyz\\ x^{2}z& xyz& x{z}^2\\ x{y}^2& y^3& y^{2}z\\ xyz& y^{2}z& y{z}^2\\ x{z}^2& y{z}^2& z^3\end{array}\right]=\left[\begin{array}{ccc}{x}_0& x_1& x_2\\ x_1& x_3& x_4\\ x_2& x_4& x_5\\ x_3& x_6& x_7\\ x_4& x_7& x_8\\ x_5& x_8& x_9\end{array}\right]$$

But then, a point $(x_0:x_1:\cdots :x_9)$ belongs to the image of ${\mathbb{P}}^2$ if (and only if) the matrix on the right-hand side has rank $1$ (that is, all its $2\times 2$ minors vanish). Next, consider the quiver

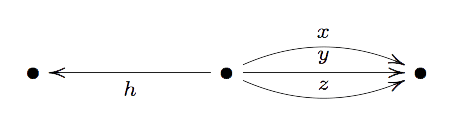
and consider the representation $V=(V_1,V_2,V_3)$ with vertex-spaces $V_1=\mathbb{C}$, $V_2={\mathbb{C}}^{10}$ and $V_2={\mathbb{C}}^6$. The linear maps $x,y$ and $z$ correspond to the columns of the matrix above, that is

$$(x_0,x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,x_9)\{\begin{array}{l}{\to }^x(x_0,x_1,x_2,x_3,x_4,x_5)\\ {\to }^y(x_1,x_3,x_4,x_6,x_7,x_8)\\ {\to }^z(x_2,x_4,x_5,x_7,x_8,x_9)\end{array}$$

The linear map $h:{\mathbb{C}}^{10}\to \mathbb{C}$ encodes the equation of the hyper-plane, that is $h=x_0-x_7+x_9$.

Now consider the quiver Grassmannian $QGr(m,V)$ for the dimension vector $m=(0,1,1)$. A base-vector $p=(x_0,\cdots ,x_9)$ of $W_2=\mathbb{C}p$ of a subrepresentation $W=(0,W_2,W_3)\subset V$ must be such that $h(x)=0$, that is, $p$ determines a point of the hyper-plane.

Likewise the vectors $x(p),y(p)$ and $z(p)$ must all lie in the one-dimensional space $W_3=\mathbb{C}$, that is, the right-hand side matrix above must have rank one and hence $p$ is a point in the image of ${\mathbb{P}}^2$ under the Veronese.

That is, $Gr(m,V)$ is isomorphic to the intersection of this image with the hyper-plane and hence is isomorphic to the elliptic curve.

The general case is similar as one can view any projective subvariety $X\to {\mathbb{P}}^n$ as isomorphic to the intersection of the image of a specific $d$-uple Veronese embedding ${\mathbb{P}}^n\to {\mathbb{P}}^N$ with a number of hyper-planes in ${\mathbb{P}}^N$.

ADDED For those desperate to read the original comments-section, here’s the link.