Skip to content →

neverendingbooks Posts

a COLgo endgame

Published January 17, 2018 by lieven

COL is a map-colouring game, attibuted to Colin Vout. COLgo is COL played with Go-stones on a go-board.

The two players, bLack (left) and white (right) take turns placing a stone of their colour on the board, but two stones of the same colour may not be next to each other.

The first player unable to make a legal move looses this game.

As is common in combinatorial game theory we do not specify which player has the move. There are $4$ different outcomes, the game is called:

– positive, if there is a winning strategy for Left (bLack),
– negative, if there is a winning strategy for Right (white),
– zero, if there is a winning strategy for the second-player,
– fuzzy, if there is a winning strategy for the first player.

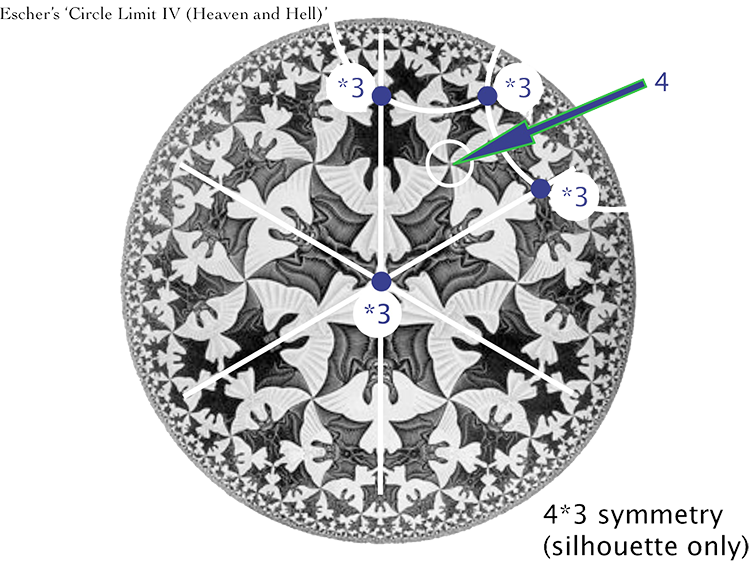
Here’s an endgame problem: who wins this game?

Spoiler alert: solution below.

First we can exclude all spots which are dead, that is, are excluded for both players. Example, F11 is dead because it neighbors a black as well as a white stone, but F10 is alive as it can be played by white (Right).

If we remove all dead spots, we are left with 4 regions (the four extremal corners of the board) as well as 5 spots, 3 for white and 2 for black.

That is, the game reduces to this “sum”-game, in which a player chooses one of the regions and does a legal move in that component, or takes a stone of its own colour from the second row.

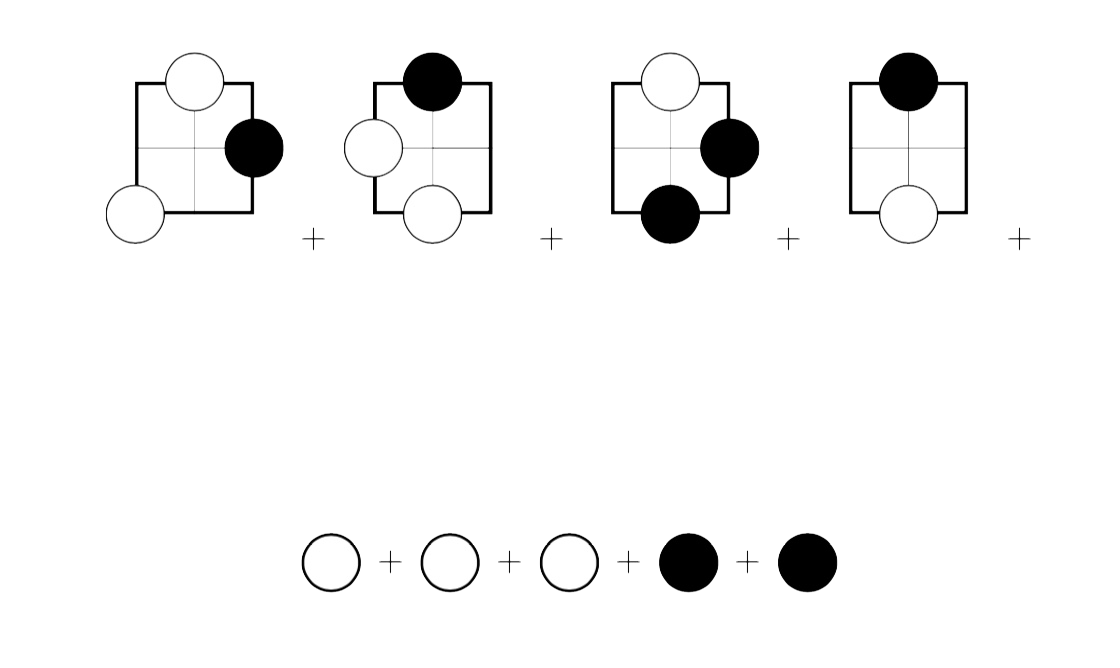
Next, we have to give a value to each of the region-games.

– the right-most game has value $0$ as the second player has a winning strategy by reflecting the first player’s move with respect to the central (dead) spot.

– the left-most game is equivalent to one black stone. Black can make two moves in the game, independent of the only move that white can make. So it has value $+1$.

– the sum-game of the two middle games has value zero. The second player can win by mirroring the first player’s move in the other component. This is called the Tweedledee-Tweedledum argument.

But then, the total value of the endgame position is

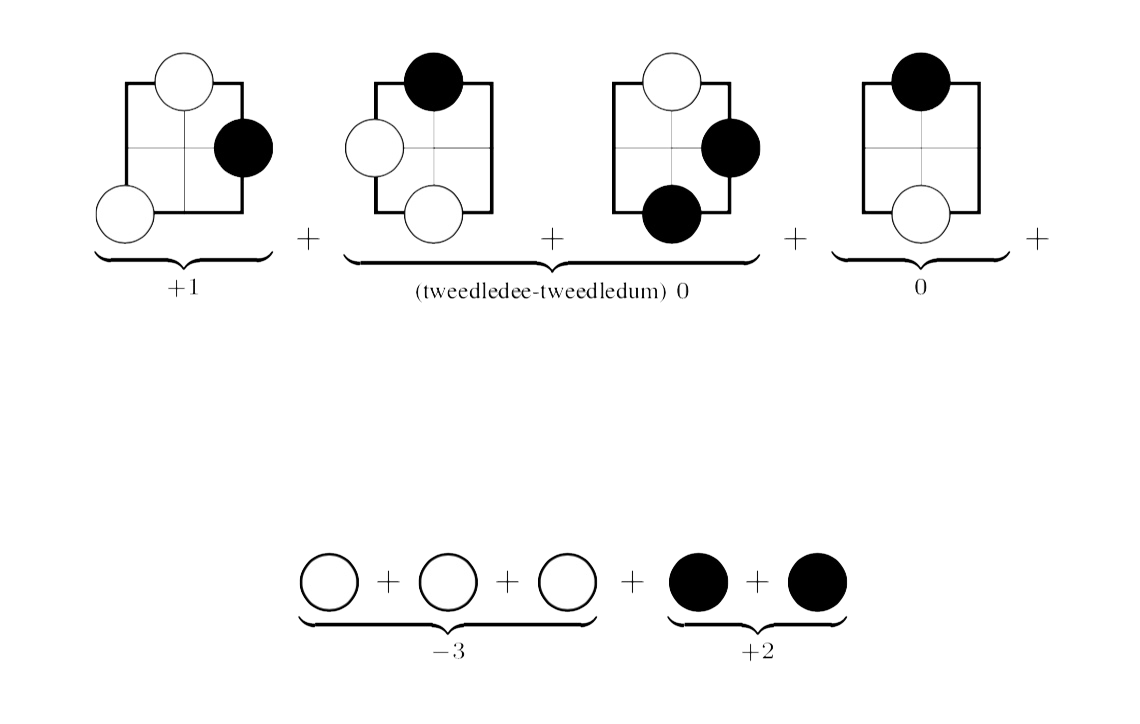
zero, so the first player to move looses the game!

Comments closed

a wintry chataigneraie

Published January 16, 2018 by lieven

It took us some time to clear the array of old chestnut trees.

But it paid off. A good harvest easily gives half a ton of chestnuts, including some rare, older varieties.

In the autumn, the coloured leaves make a spectacular view. Now it looks rather desolate.

But, the wind piles up the fallen leaves in every nook, cranny, corner or entrance possible.

My day in the mountains: ‘harvesting’ fallen leaves…

Comments closed

Coxeter on Escher’s Circle Limits

Published January 15, 2018 by lieven

Conway’s orbifold notation gives a uniform notation for all discrete groups of isometries of the sphere, the Euclidian plane as well as the hyperbolic plane.

This includes the groups of symmetries of Escher’s Circle Limit drawings. Here’s Circle Limit III

And ‘Angels and Devils’ aka Circle Limit IV:

If one crawls along a mirror of this pattern until one hits another mirror and then turns right along this mirror and continues like this, you get a quadrilateral path with four corners $\frac{\pi}{3}$, whose center seems to be a $4$-fold gyration point. So, it appears to have symmetry $4 \ast 3$.


(image credit: MathCryst)

However, looking more closely, every fourth figure (either devil or angel) is facing away rather than towards us, so there’s no gyration point, and the group drops to $\ast 3333$.

Harold S. M. Coxeter met Escher in Amsterdam at the ICM 1954.

The interaction between the two led to Escher’s construction of the Circle Limits, see How did Escher do it?

Here’s an old lecture by Coxeter on the symmetry of the Circle Limits:



Comments closed