Klein’s
quartic $X$is the smooth plane projective curve defined by
$x^3y+y^3z+z^3x=0$ and is one of the most remarkable mathematical
objects around. For example, it is a Hurwitz curve meaning that the
finite group of symmetries (when the genus is at least two this group
can have at most $84(g-1)$ elements) is as large as possible, which in
the case of the quartic is $168$ and the group itself is the unique
simple group of that order, $G = PSL_2(\mathbb{F}_7)$ also known as
Klein\’s group. John Baez has written a [beautiful page](http://math.ucr.edu/home/baez/klein.html) on the Klein quartic and
its symmetries. Another useful source of information is a paper by Noam
Elkies [The Klein quartic in number theory](www.msri.org/publications/books/Book35/files/elkies.pd).
The quotient map $X \rightarrow X/G \simeq \mathbb{P}^1$ has three
branch points of orders $2,3,7$ in the points on $\mathbb{P}^1$ with
coordinates $1728,0,\infty$. These points correspond to the three
non-free $G$-orbits consisting resp. of $84,56$ and $24$ points.
Now, remove from $X$ a couple of $G$-orbits to obtain an affine open
subset $Y$ such that $G$ acts on its cordinate ring $\mathbb{C}[Y]$ and
form the Klein stack (or hereditary order) $\mathbb{C}[Y] \bigstar G$,
the skew group algebra. In case the open subset $Y$ contains all
non-free orbits, the [one quiver](lievenlb.local/master/coursenotes/onequiver.pdf) of this
qurve has the following shape $\xymatrix{\vtx{} \ar@/^/[dd] \\
\\ \vtx{} \ar@/^/[uu]} $ $\xymatrix{& \vtx{} \ar[ddl] & \\
& & \\ \vtx{} \ar[rr] & & \vtx{} \ar[uul]} $ $\xymatrix{& &
\vtx{} \ar[dll] & & \\ \vtx{} \ar[d] & & & & \vtx{} \ar[ull] \\ \vtx{}
\ar[dr] & & & & \vtx{} \ar[u] \\ & \vtx{} \ar[rr] & & \vtx{} \ar[ur]
&} $ Here, the three components correspond to the three
non-free orbits and the vertices correspond to the isoclasses of simple
$\mathbb{C}[Y] \bigstar G$ of dimension smaller than $168$. There are
two such of dimension $84$, three of dimension $56$ and seven of
dimension $24$ which I gave the non-imaginative names \’twins\’,
\’trinity\’ and \’the dwarfs\’. As we want to spice up later this
Klein stack to a larger group, we need to know the structure of these
exceptional simples as $G$-representations. Surely, someone must have
written a paper on the general problem of finding the $G$-structure of
simples of skew-group algebras $A \bigstar G$, so if you know a
reference please let me know. I used an old paper by Idun Reiten and
Christine Riedtmann to do this case (which is easier as the stabilizer
subgroups are cyclic and hence the induced representations of their
one-dimensionals correspond to the exceptional simples).
neverendingbooks Posts
I got
Tracks working under Tiger by trial and error starting with a suggestion
from Jan who found a fix here. From this I stumbled on for an hour or so on my iMac
untill near the very end I found that the tracks-page itself now
has a Tiger-section. So, let’s try to do it all over again from fresh on
my regular machine (a little iBook).
Start with
this page and read it all the way to the comments. There is a
comment by Jamie on installing Rails and MySQL on a fresh Tiger which
looks like the thing I want followed immediately by another post by Jose
Marinez on
Installing Ruby on Rails on Tiger which I decided to follow by the
letter (with one noticeable exception!). So first I downloaded the Rails
installer on Tiger. Next, an install of the Standard version of
MySQL. I used version 4.0 for OS
X 10.3 !!!! NOT 4.1 !!!!. I installed MySQL and the StartUpItem.
Next, I opened Terminal and typed the following commands
– cd
/usr/local/mysql
– sudo chown -R mysql data/
– sudo echo
– sudo ./bin/mysqld_safe &
and verified it by performing a
simple test
/usr/local/mysql/bin/mysql test
Next, I
secured everything by having a root-password
/usr/local/mysql/bin/mysqladmin -u root password
__*
Then I remembered that I’d better
not have to type the whole path so I did a
echo ‘export
PATH=/usr/local/mysql/bin:$PATH’ >> ~/.bash_profile
Also, I want
to admin MySQL via phpmyadmin so I
installed it. Then I enabled my webserver to use PHP using this post though I
did use vi rather than pico! Next, i did a check whether everything
worked fine by typing in safari
http://localhost/~lieven/phpmyadmin/index.php
Followed by
a
sudo gem install mysql –
–with-mysql-dir=/usr/local/mysql
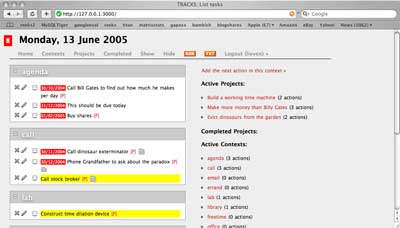
Now, it is time to get the Tracks-package
and to follow these instructions And, it works! Here is the proof :
Here the
story of an idea to construct new examples of non-commutative compact
manifolds, the computational difficulties one runs into and, when they
are solved, the white noise one gets. But, perhaps, someone else can
spot a gem among all gibberish…
[Qurves](https://lievenlb.local/toolkit/pdffile.php?pdf=/TheLibrary/papers/qaq.pdf) (aka quasi-free algebras, aka formally smooth
algebras) are the \’affine\’ pieces of non-commutative manifolds. Basic
examples of qurves are : semi-simple algebras (e.g. group algebras of
finite groups), [path algebras of
quivers](http://www.lns.cornell.edu/spr/2001-06/msg0033251.html) and
coordinate rings of affine smooth curves. So, let us start with an
affine smooth curve $X$ and spice it up to get a very non-commutative
qurve. First, we bring in finite groups. Let $G$ be a finite group
acting on $X$, then we can form the skew-group algebra $A = \mathbfk[X]
\bigstar G$. These are examples of prime Noetherian qurves (aka
hereditary orders). A more pompous way to phrase this is that these are
precisely the [one-dimensional smooth Deligne-Mumford
stacks](http://www.math.lsa.umich.edu/~danielch/paper/stacks.pdf).
As the 21-st century will turn out to be the time we discovered the
importance of non-Noetherian algebras, let us make a jump into the
wilderness and consider the amalgamated free algebra product $A =
(\mathbf k[X] \bigstar G) \ast_{\mathbf k G} \mathbfk H$ where $G
\subset H$ is an interesting extension of finite groups. Then, $A$ is
again a qurve on which $H$ acts in a way compatible with the $G$-action
on $X$ and $A$ is hugely non-commutative… A very basic example :
let $\mathbb{Z}/2\mathbb{Z}$ act on the affine line $\mathbfk[x]$ by
sending $x \mapsto -x$ and consider a finite [simple
group](http://mathworld.wolfram.com/SimpleGroup.html) $M$. As every
simple group has an involution, we have an embedding
$\mathbb{Z}/2\mathbb{Z} \subset M$ and can construct the qurve
$A=(\mathbfk[x] \bigstar \mathbb{Z}/2\mathbb{Z}) \ast_{\mathbfk
\mathbb{Z}/2\mathbb{Z}} \mathbfk M$ on which the simple group $M$ acts
compatible with the involution on the affine line. To study the
corresponding non-commutative manifold, that is the Abelian category
$\mathbf{rep}~A$ of all finite dimensional representations of $A$ we have
to compute the [one quiver to rule them
all](https://lievenlb.local/master/coursenotes/onequiver.pdf) for
$A$. Because $A$ is a qurve, all its representation varieties
$\mathbf{rep}_n~A$ are smooth affine varieties, but they may have several
connected components. The direct sum of representations turns the set of
all these components into an Abelian semigroup and the vertices of the
\’one quiver\’ correspond to the generators of this semigroup whereas
the number of arrows between two such generators is given by the
dimension of $Ext^1_A(S_i,S_j)$ where $S_i,S_j$ are simple
$A$-representations lying in the respective components. All this
may seem hard to compute but it can be reduced to the study of another
quiver, the Zariski quiver associated to $A$ which is a bipartite quiver
with on the left the \’one quiver\’ for $\mathbfk[x] \bigstar
\mathbb{Z}/2\mathbb{Z}$ which is just $\xymatrix{\vtx{}
\ar@/^/[rr] & & \vtx{} \ar@/^/[ll]} $ (where the two vertices
correspond to the two simples of $\mathbb{Z}/2\mathbb{Z}$) and on the
right the \’one quiver\’ for $\mathbf k M$ (which just consists of as
many verticers as there are simple representations for $M$) and where
the number of arrows from a left- to a right-vertex is the number of
$\mathbb{Z}/2\mathbb{Z}$-morphisms between the respective simples. To
make matters even more concrete, let us consider the easiest example
when $M = A_5$ the alternating group on $5$ letters. The corresponding
Zariski quiver then turns out to be $\xymatrix{& & \vtx{1} \\\
\vtx{}\ar[urr] \ar@{=>}[rr] \ar@3[drr] \ar[ddrr] \ar[dddrr] \ar@/^/[dd]
& & \vtx{4} \\\ & & \vtx{5} \\\ \vtx{} \ar@{=>}[uurr] \ar@{=>}[urr]
\ar@{=>}[rr] \ar@{=>}[drr] \ar@/^/[uu] & & \vtx{3} \\\ & &
\vtx{3}} $ The Euler-form of this quiver can then be used to
calculate the dimensions of the EXt-spaces giving the number of arrows
in the \’one quiver\’ for $A$. To find the vertices, that is, the
generators of the component semigroup we have to find the minimal
integral solutions to the pair of equations saying that the number of
simple $\mathbb{Z}/2\mathbb{Z}$ components based on the left-vertices is
equal to that one the right-vertices. In this case it is easy to see
that there are as many generators as simple $M$ representations. For
$A_5$ they correspond to the dimension vectors (for the Zariski quiver
having the first two components on the left) $\begin{cases}
(1,2,0,0,0,0,1) \\ (1,2,0,0,0,1,0) \\ (3,2,0,0,1,0,0) \\
(2,2,0,1,0,0,0) \\ (1,0,1,0,0,0,0) \end{cases}$ We now have all
info to determine the \’one quiver\’ for $A$ and one would expect a nice
result. Instead one obtains a complete graph on all vertices with plenty
of arrows. More precisely one obtains as the one quiver for $A_5$
$\xymatrix{& & \vtx{} \ar@{=}[dll] \ar@{=}[dddl] \ar@{=}[dddr]
\ar@{=}[drr] & & \\\ \vtx{} \ar@(ul,dl)|{4} \ar@{=}[rrrr]|{6}
\ar@{=}[ddrrr]|{8} \ar@{=}[ddr]|{4} & & & & \vtx{} \ar@(ur,dr)|{8}
\ar@{=}[ddlll]|{6} \ar@{=}[ddl]|{10} \\\ & & & & & \\\ & \vtx{}
\ar@(dr,dl)|{4} \ar@{=}[rr]|{8} & & \vtx{} \ar@(dr,dl)|{11} & } $
with the number of arrows (in each direction) indicated. Not very
illuminating, I find. Still, as the one quiver is symmetric it follows
that all quotient varieties $\mathbf{iss}_n~A$ have a local Poisson
structure. Clearly, the above method can be generalized easily and all
examples I did compute so far have this \’nearly complete graph\’
feature. One might hope that if one would start with very special
curves and groups, one might obtain something more interesting. Another
time I\’ll tell what I got starting from Klein\’s quartic (on which the
simple group $PSL_2(\mathbb{F}_7)$ acts) when the situation was sexed-up
to the sporadic simple Mathieu group $M_{24}$ (of which
$PSL_2(\mathbb{F}_7)$ is a maximal subgroup).