Monsieur Mathieu

Even a virtual course needs an opening line, so here it is : Take your favourite $S{L}_2(\mathbb{Z})$-representation Here is mine : the permutation presentation of the Mathieu group(s). Emile Leonard Mathieu is remembered especially for his discovery (in 1861 and 1873) of five sporadic simple groups named after him, the Mathieu groups $M_{11},M_{12},M_{22},M_{23}$ and $M_{24}$. These were studied in his thesis on transitive functions. He had a refreshingly direct style
of writing. I’m not sure what Cauchy would have thought (Cauchy died in 1857) about this ‘acknowledgement’ in his 1861-paper in which Mathieu describes $M_{12}$ and claims the construction of $M_{24}$.

Also the opening sentenses of his 1873 paper are nice, something along the lines of “if no expert was able to fill in the details of my claims made twelve years ago, I’d better do it myself”.

However, even after this paper opinions remained divided on the issue whether or not he did really achieve his goal, and the matter was settled decisively by Ernst Witt connecting the Mathieu groups to Steiner systems (if I recall well from Mark Ronan’s book Symmetry and the monster)

As Mathieu observed, the quickest way to describe these groups would be to give generators, but as these groups are generated by two permutations on 12 respectively 24 elements, we need to have a mnemotechnic approach to be able to reconstruct them whenever needed.

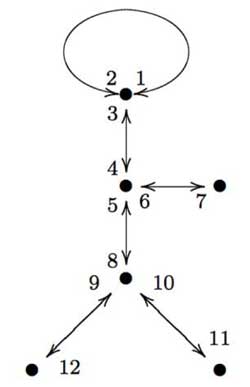
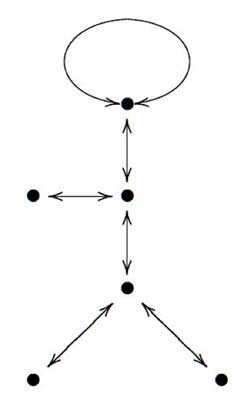
Here is a nice approach, due to Gunther Malle in a Luminy talk in 1993 on “Dessins d’enfants” (more about them later). Consider the drawing of “Monsieur Mathieu” on the left. That is, draw the left-handed bandit picture on 6 edges and vertices, divide each edge into two and give numbers to both parts (the actual numbering is up to you, but for definiteness let us choose the one on the left). Then, $M_{12}$ is generated by the order two permutation describing the labeling of both parts of the edges

$s=(1,2)(3,4)(5,8)(7,6)(9,12)(11,10)$

together with the order three permutation obtained from cycling counterclockwise
around a trivalent vertex and calling out the labels one encounters. For example, the three cycle corresponding to the ‘neck vertex’ is $(1,2,3)$ and the total permutation
is

$t=(1,2,3)(4,5,6)(8,9,10)$

A quick verification using GAP tells that these elements do indeed generate a simple group of order 95040.

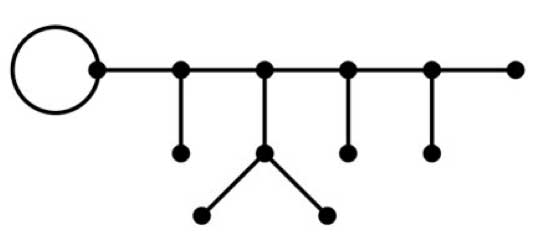
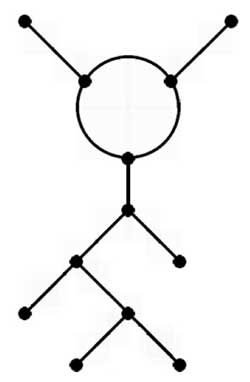
Similarly, if you have to reconstruct the largest Mathieu group from scratch, apply the same method to the the picture above or to “ET Mathieu” drawing on the left. This picture I copied from Alexander Zvonkin‘s paper How to draw a group as well as the computational details below.

This is all very nice and well but what do these drawings have to do with Grothendieck’s “dessins d’enfants”? Consider the map from the projective line onto itself

${\mathbb{P}}_{\mathbb{C}}^1\to {\mathbb{P}}_{\mathbb{C}}^1$

defined by the rational map

$f(z)=\frac{(z^3-z^2+az+b{)}^3(z^3+c{z}^2+dz+e)}{Kz}$

where N. Magot calculated that

$a=\frac{107+7\sqrt{-11}}{486},b=-\frac{13}{567}a+\frac{5}{1701},c=-\frac{17}{9},d=\frac{23}{7}a+\frac{256}{567},e=-\frac{1573}{567}a+\frac{605}{1701}$

and finally

$K=-\frac{16192}{301327047}a+\frac{10880}{903981141}$

One verifies that this map is 12 to 1 everywhere except over the points $0,1,\mathrm{\infty }$ (that is, there are precisely 12 points mapping under f to a given point of ${\mathbb{P}}_{\mathbb{C}}^1–0,1,\mathrm{\infty }$. From the expression of f(z) it is clear that over 0 there lie 6 points (3 of which with multiplicity three, the others of multiplicity one). Over $\mathrm{\infty }$ there are two points, one with multiplicity 11 and one with multiplicity one. The difficult part is to compute the points lying over 1. The miraculous fact of the given values is that

$f(z)-1=\frac{-B(z{)}^2}{Kz}$

where

$B(z)=z^6+\frac{1}{11}(10c-8)z^5+(5a+9d-7c)z^4+(2b+4ac+8e-6d)z^3+$
$(3ad+bc-5e)z^2+2aez-be)$

and hence there are 6 points lying over 1 each with mutiplicity two.

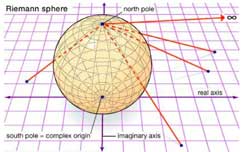
Right, now consider the complex projective line ${\mathbb{P}}_{\mathbb{C}}^1$ as the Riemann sphere $S^2$ and mark the six points lying over 1 by a white vertex and the six points lying over 0 with a black vertex (in the source sphere). Now, lift the real interval $[0,1]$ in the target sphere ${\mathbb{P}}_{\mathbb{C}}^1=S^2$ to its inverse image on the source sphere. As there are exactly 12 points lying over each real
number $0⪇r⪇1$, this inverse image will consist of 12 edges which are noncrossing and each end in one black and one white vertex. The obtained graph will look like the \”Monsieur Mathieu\” drawing above with the vertices corresponding to the black vertices and the three points over 1 of multiplicity three corresponding to the
trivalent vertices, those of multiplicity one to the three end-vertices. The white vertices correspond to mid-points of the six edges, so that we do get a drawing with twelve edges, one corresponding to each number. From the explicit description of f(z) it is clear that this map is defined over $\mathbb{Q}\sqrt{-11}$ which is also the
smallest field containing all character-values of the Mathieu group $M_{12}$. Further, the Galois group of the extension $Gal(\mathbb{Q}\sqrt{-11}/\mathbb{Q})=\mathbb{Z}/2\mathbb{Z}$ and is generated by complex conjugation. So, one might wonder what would happen if we replaced in the definition of the rational map f(z) the value of a by $a=\frac{107-\sqrt{-11}}{486}$. It turns out that this modified map has the same properties as $f(z)$ so again one can draw on the source sphere a picture consisting of twelve edges each ending in a white and black vertex.

If we consider the white vertices (which incidentally each lie on two edges as all points lying over 0 are of multiplicity two) as mid-points of longer edges connecting the
black vertices we obtain a drawing on the sphere which looks like \”Monsieur Mathieu\” but this time as a right handed bandit, and applying our mnemotechnic rule we obtain _another_ (non conjugated) embedding of $M_{12}$ in the full symmetric group on 12 vertices.

What is the connection with $S{L}_2(\mathbb{Z})$-representations? Well, the permutation generators s and t of $M_{12}$ (or $M_{24}$ for that matter) have orders two and three, whence there is a projection from the free group product $C_2\star C_3$ (here $C_n$ is just the cyclic group of order n) onto $M_{12}$ (respectively $M_{24}$). Next
time we will say more about such free group products and show (among other things) that $PS{L}_2(\mathbb{Z})\simeq C_2\star C_3$ whence the connection with $S{L}_2(\mathbb{Z})$. In a following lecture we will extend the Monsieur Mathieu example to
arbitrary dessins d\’enfants which will allow us to assign to curves defined over $\bar{\mathbb{Q}}$ permutation representations of $S{L}_2(\mathbb{Z})$ and other _cartographic groups_ such as the congruence subgroups ${\mathrm{\Gamma }}_0(2)$ and
$\mathrm{\Gamma }(2)$.