Bruce Westbury has a page on recent work on series of Lie groups including exceptional groups. Moreover, he did put his slides of a recent talk (probably at MPI) online.
Probably, someone considered a similar problem for simple groups. Are there natural constructions leading to a series of finite simple groups including some sporadic groups as special members ? In particular, does the following sequence appear somewhere ?
$L_2(7), M_{12}, A_{16}, M_{24}, A_{28}, A_{40}, A_{48}, A_{60}, \ldots $
Here, $L_2(7) $ is the simple group of order 168 (the automorphism group of the Klein quartic), $M_{12} $ and $M_{24} $ are the sporadic Mathieu groups and the $A_n $ are the alternating simple groups.
I’ve stumbled upon this series playing around with Farey sequences and their associated ‘dessins d’enfants’ (I’ll come back to the details of the construction another time) and have dubbed this sequence the Iguanodon series because the shape of the doodle leading to its first few terms
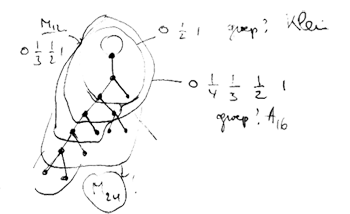
reminded me of the Iguanodons of Bernissart (btw. this sketch outlines the construction to the experts). Conjecturally, all groups appearing in this sequence are simple and probably all of them (except for the first few) will be alternating.
I did verify that none of the known low-dimensional permutation representations of other sporadic groups appear in the series. However, there are plenty of similar sequences one can construct from the Farey sequences, and it would be nice if one of them would contain the Conway group $Co_1 $. (to be continued)
Comments