How to dismantle scheme theory?

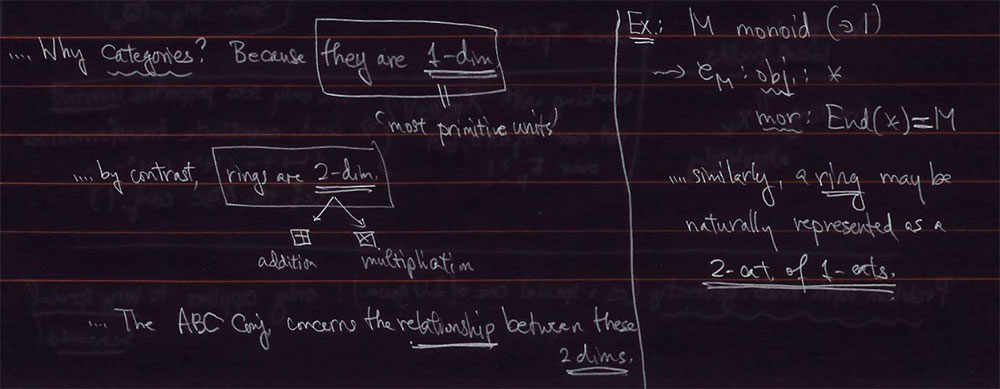
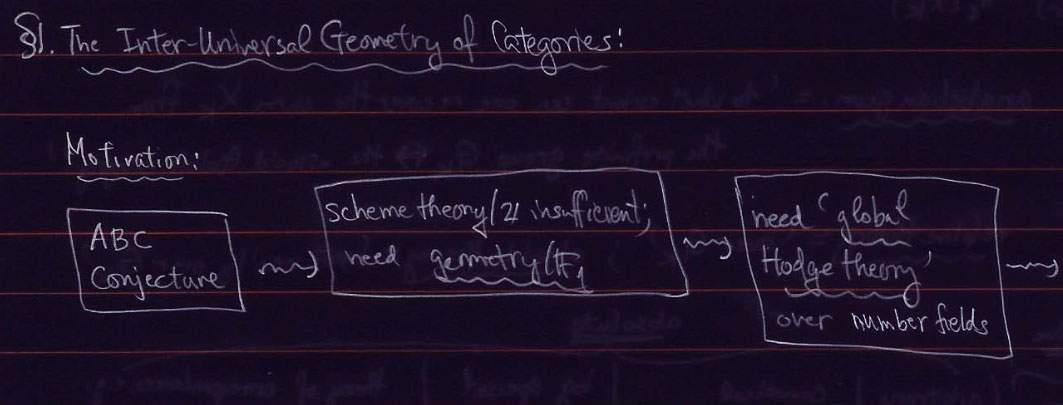
In several of his talks on #IUTeich, Mochizuki argues that usual scheme theory over $\mathbb{Z}$ is not suited to tackle problems such as the ABC-conjecture.

The idea appears to be that ABC involves both the additive and multiplicative nature of integers, making rings into ‘2-dimensional objects’ (and clearly we use both ‘dimensions’ in the theory of schemes).

So, perhaps we should try to ‘dismantle’ scheme theory, and replace it with something like geometry over the field with one element ${\mathbb{F}}_1$.

The usual ${\mathbb{F}}_1$ mantra being: ‘forget all about the additive structure and only retain the multiplicative monoid’.

So perhaps there is yet another geometry out there, forgetting about the multiplicative structure, and retaining just the addition…

This made me wonder.

In the forgetting can’t be that hard, can it?-post we have seen that the forgetful functor

$$F_{+,\times }:\mathbf{rings}\to \mathbf{sets}$$

(that is, forgetting both multiplicative and additive information of the ring) is representable by the polynomial ring $\mathbb{Z}[x]$.

So, what about our ‘dismantling functors’ in which we selectively forget just one of these structures:

$$F_{+}:\mathbf{rings}\to \mathbf{monoids}\text{and}{F}_{\times }:\mathbf{rings}\to \mathbf{abelian}\mathbf{groups}$$

Are these functors representable too?

Clearly, ring maps from $\mathbb{Z}[x]$ to our ring $R$ give us again the elements of $R$. But now, we want to encode the way two of these elements add (or multiply).

This can be done by adding extra structure to the ring $\mathbb{Z}[x]$, namely a comultiplication $\mathrm{\Delta }$ and a counit $ϵ$

$$\mathrm{\Delta }:\mathbb{Z}[x]\to \mathbb{Z}[x]\otimes \mathbb{Z}[x]\text{and}ϵ:\mathbb{Z}[x]\to \mathbb{Z}$$

The idea of the comultiplication being that if we have two elements $r,s\in R$ with corresponding ring maps $f_r:\mathbb{Z}[x]\to Rx\mapsto r$ and $f_s:\mathbb{Z}[x]\to Rx\mapsto s$, composing their tensorproduct with the comultiplication

$$f_v:\mathbb{Z}[x]{\to }^{\mathrm{\Delta }}\mathbb{Z}[x]\otimes \mathbb{Z}[x]{\to }^{f_r\otimes f_s}R$$

determines another element $v\in R$ which we can take either the product $v=r.s$ or sum $v=r+s$, depending on the comultiplication map $\mathrm{\Delta }$.

The role of the counit is merely sending $x$ to the identity element of the operation.

Thus, if we want to represent the functor forgetting the addition, and retaining the multiplication we have to put on $\mathbb{Z}[x]$ the structure of a biring

$$\mathrm{\Delta }(x)=x\otimes x\text{and}ϵ(x)=1$$

(making $x$ into a ‘group-like’ element for Hopf-ists).

The functor $F_{\times }$ forgetting the multiplication but retaining the addition is represented by the Hopf-ring $\mathbb{Z}[x]$, this time with

$$\mathrm{\Delta }(x)=x\otimes 1+1\otimes x\text{and}ϵ(x)=0$$

(that is, this time $x$ becomes a ‘primitive’ element).

Perhaps this adds another feather of weight to the proposal in which one defines algebras over the field with one element ${\mathbb{F}}_1$ to be birings over $\mathbb{Z}$, with the co-ring structure playing the role of descent data from $\mathbb{Z}$ to ${\mathbb{F}}_1$.

As, for example, in my note The coordinate biring of $\mathbf{Spec}(\mathbb{Z})/{\mathbb{F}}_1$.