Last week, Melanie Raczek gave a talk entitled ‘Cubic forms and Okubo product’ in our Artseminar, based on her paper On ternary cubic forms that determine central simple algebras of degree 3.
I had never heard of this strange non-associative product on 8-dimensional space, but I guess it is an instance of synchronicity that now the Okubo algebra seems to pop-up everywhere.
Yesterday, there was the post the Okubo algebra by John Baez at the n-cafe, telling that Susumu Okubo discovered his algebra while investigating quarks.
I don’t know a thing about the physics, but over the last days I’ve been trying to understand some of the miraculous geometry associated to the Okubo algebra. So, let’s start out by defining the ‘algebra’.
Consider the associative algebra of all 3×3 complex matrices $M_3(\mathbb{C}) $ with the usual matrix-multiplication. In this algebra there is the 8-dimensional subspace of trace zero matrices, usually called the Lie algebra $\mathfrak{sl}_3 $. However, we will not use the Lie-bracket, only matrix-multiplication. Typical elements of $\mathfrak{sl}_3 $ will be written as $X,Y,Z,… $ and their entries will be denoted as
$X = \begin{bmatrix} x_0 & x_1 & x_2 \\ x_3 & x_4 & x_5 \\ x_6 & x_7 & -x_0-x_4 \end{bmatrix} $
For any two elements $X,Y \in \mathfrak{sl}_3 $ one defines their Okubo-product to be the 3×3 matrix
$X \ast Y = \frac{1}{1-\omega}(Y.X-\omega X.Y) – \frac{1}{3}Tr(X.Y) 1_3 $
where $\omega $ is a primitive 3-rd root of unity and $1_3 $ is the identity matrix. Written out in the entries of X and Y this operation looks horribly complicated
$X \ast Y = \frac{1}{1-\omega} \begin{bmatrix} p_{11} & p_{12} & p_{13} \\ p_{21} & p_{22} & p_{23} \\ p_{31} & p_{32} & -p_{11}-p_{22} \end{bmatrix} $
with
[tex]\begin{eqalign} \\ p_{11} &= (1-\omega)x_0y_0+x_3y_1+x_6y_2-\omega(x_1y_3+x_2y_6)-\frac{1}{3}T \\ p_{12} &= x_1y_0+x_4y_1+x_7y_2-\omega(x_0y_1+x_1y_4+x_2y_7) \\ p_{13} &= x_2y_0+x_5y_1-x_0y_2-x_4y_2-\omega(x_0y_2+x_1y_5-x_2y_0-x_2y_4) \\
p_{21} &= x_0y_3+x_3y_4+x_6y_5 – \omega(x_3y_0+x_4y_3+x_5y_6) \\
p_{22} &= (1-\omega)x_4y_4+x_1y_3+x_7y_5 – \omega(x_3y_1+x_5y_7) – \frac{1}{3}T \\
p_{23} &= x_2y_3+x_5y_4-x_0y_5-x_4y_5-\omega(x_3y_2+x_4y_5-x_5y_0-x_5y_4) \\
p_{31} &= x_0y_6+x_3y_7-x_6y_0-x_6y_4-\omega(x_6y_0+x_7y_3-x_0y_6-x_4y_6) \\
p_{32} &= x_1y_6+x_4y_7-x_7y_0-x_7y_4 – \omega(x_6y_1+x_7y_4-x_0y_7-x_4y_7) \\
T &= 2x_0y_0+2x_4y_4+x_1y_3+x_2y_6+x_3y_1+x_5y_7+x_6y_2+x_7y_5+x_0y_4+x_4y_0
\end{eqalign}[/tex]
The crucial remark to make is that $X \ast Y $ is again a trace zero matrix. That is, we have defined a new operation on $\mathfrak{sl}_3 $.
$\mathfrak{sl}_3 \times \mathfrak{sl}_3 \rightarrow \mathfrak{sl}_3~\qquad~\qquad~(X,Y) \mapsto X \ast Y $
This Okubo-product is neither a Lie-bracket, nor an associative multiplication. In fact, it is a lot ‘less associative’ than that other 8-dimensional algebra, the octonions. The only noteworthy identity it has is that $X \ast (Y \ast X) = (X \ast Y) \ast X $. So, why should we be interested in this horrible algebra?
Well, let us consider the subset of $\mathfrak{sl}_3 $ consisting of those matrices X satusfying $Tr(X^2)=0 $. That is, with the above notation, all matrices X such that
$x_0^2+x_4^2+x_1x_3+x_2x_6+x_5x_7=0 $
In the 8-dimensional affine space $\mathfrak{sl}_3 $ these matrices form a singular quadric with top the zero-matrix. So, it is better to go projective. That is, any non-zero matrix $X \in \mathfrak{sl}_3 $ determines a point in 7-dimensional projective space $\mathbb{P}^7 $ with homogeneous coordinates
$\overline{X} = [x_0:x_1:x_2:x_3:x_4:x_5:x_6:x_7] \in \mathbb{P}^7 $
and the points $\overline{X} $ corresponding to solutions of $Tr(X^2)=0 $ form a smooth 6-dimensional quadric $Q \subset \mathbb{P}^7 $ with homogeneous equation
$Q = \mathbb{V}(x_0^2+x_4^2+x_1x_3+x_2x_6+x_5x_7) $
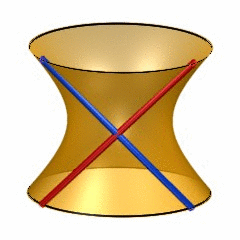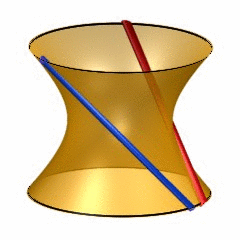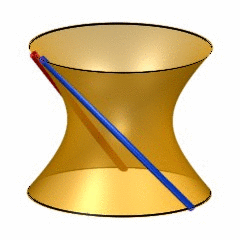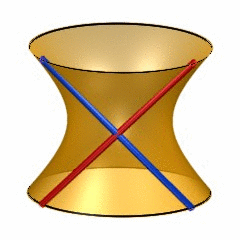6-dimensional quadrics may be quite hard to visualize, so it may help to recall the classic situation of lines on a 2-dimensional quadric (animated gif taken from surfex).
A 2-dimensional quadric contains two families of lines, often called the ‘blue lines’ and the ‘red lines’, each of these lines isomorphic to $\mathbb{P}^1 $. The rules-of-intersection of these are :
- different red lines are disjoint as are different blue lines
- any red and any blue line intersect in exactly one point
- every point of the quadric lies on exactly one red and one blue line
The lines in either family are in one-to-one correspondence with the points on the projective line. We therefore say that there is a $\mathbb{P}^1 $-family of red lines and a $\mathbb{P}^1 $-family of blue lines on a 2-dimensional quadric.
A 6-dimensional quadric $Q \subset \mathbb{P}^7 $ contains two families of ‘3-planes’. That is, there is a family of red $\mathbb{P}^3 $’s contained in Q and a family of blue $\mathbb{P}^3 $’s. Can we determine these red and blue 3-planes explicitly?
Yes we can, using the Okubo algebra-product on $\mathfrak{sl}_3 $. Take $X \in \mathfrak{sl}_3 $ defining the point $\overline{X} \in Q $ (that is, $Tr(X^2)=0 $). then all 3×3 matrices one obtains by taking the Okubo-product with left X-factor form a 4-dimensional linear subspace in $\mathfrak{sl}_3 $
$L_X = { X \ast Y~|~Y \in \mathfrak{sl}_3 } \simeq \mathbb{C}^4 \subset \mathfrak{sl}_3 $
so its non-zero matrices determine a 3-plane in $\mathbb{P}^7 $ (consisting of all points with homogeneous coordinates $[p_{11}:p_{12}:p_{13}:p_{21}:p_{22}:p_{23}:p_{31}:p_{32}] $, using the above formulas) which actually lies entirely in the quadric Q. These are precisely the bLue 3-planes in Q. That is, the family of all bLue 3-planes consists precisely of the 3-planes
$\mathbb{P}(L_X) $ with $X \in \mathfrak{sl}_3 $ satisfying $Tr(X^2)=0 $
Phrased differently, any point $\overline{X} \in Q $ determines a blue 3-plane $\mathbb{P}(L_X) $.
Similarly, any point $\overline{X} \in Q $ determines a Red 3-plane by taking Okubo-products with Right X-factor, that is, $\mathbb{P}(R_X) $ is a 3-plane for Q where
$R_X = { Y \ast X~|~Y \in \mathfrak{sl}_3 } \simeq \mathbb{C}^4 \subset \mathfrak{sl}_3 $
and all Red 3-planes for Q are of this form. But, this is not all… these correspondences are unique! That is, any point on the quadric defines a unique red and a unique blue 3-plane, or, phrased differently, there is a Q-family of red 3-planes and a Q-family of blue 3-planes in Q. This is a consequence of triality.
To see this, note that the automorphism group of a 6-dimensional smooth quadric is the rotation group $SO_8(\mathbb{C}) $ and this group has Dynkin diagram $D_4 $, the most symmetrical of them all!
In general, every node in a Dynkin diagram has an interesting projective variety associated to it, a so called homogeneous space. I’ll just mention what these spaces are corresponding to the 4 nodes of $D_4 $. Full details can be found in chapter 23 of Fulton and Harris’ Representation theory, a first course.
The left-most node corresponds to the orthogonal Grassmannian of isotropic 1-planes in $\mathbb{C}^8 $ which is just a fancy way of viewing our quadric Q. The two right-most nodes correspond to the two connected components of the Grassmannians of isotropic 4-planes in $\mathbb{C}^8 $, which are our red resp. blue families of 3-planes on the quadric. Now, as the corresponding dotted Dynkin diagrams are isomorphic
there corresponding homogeneous spaces are also isomorphic. Thus indeed, there is a one-to-one correspondence between points of the quadric Q and red 3-planes on Q (and similarly with blue 3-planes on Q).
Okay, so the Okubo-product allows us to associate to a point on the 6-dimensional quadric Q a unique red 3-plane and a unique blue 3-plane (much as any point on a 2-dimensional quadric determines a unique red and blue line). Do these families of red and blue 3-planes also satisfy ‘rules-of-intersection’?
Yes they do and, once again, the Okubo-product clarifies them. Here they are :
- two different red 3-planes intersect in a unique line (as do different blue 3-planes)
- the bLue 3-plane $\mathbb{P}(L_X) $ intersects the Red 3-plane $\mathbb{P}(R_Y) $ in a unique point if and only if the Okubo-product $X \ast Y \not= 0 $
- the bLue 3-plane $\mathbb{P}(L_X) $ intersects the Red 3-plane $\mathbb{P}(R_Y) $ in a unique 2-plane if and only if the Okubo-product $X \ast Y = 0 $
That is, Right and Left Okubo-products determine the Red and bLue families of 3-planes on the 6-dimensional quadric as well as their intersections!