G+ recovery 3 : #IUTeich (1)

Perhaps the ‘hottest’ topic I got involved with on Google+ was Mochizuki’s (claimed) proof of the ABC-conjecture.

Rereading these posts in chronological order shows my changing attitude to this topic, from early skepticism, over attempts to understand at least one pre-IUTeich paper (Frobenioids 1) to a level of belief, to … resignation.

Here’s the first batch of #IUTeich posts (here IUTeich stands for Mochizuki’s ‘Inter Universal Teichmuller theory).

June 12th, 2012

Linked post: ABC conjecture rumor at the Secret Blogging Seminar.

My understanding is that Google+ is for spreading (or debunking) such rumours. Sure would love to have more details!

May 26th, 2013

The Mochizuki craze continues…
Now Ted Nelson claims Mochizuki must be none other than the mysterious Satoshi Nakamoto, inventor of BitCoin.
I’ve seen BitCoin explained in 60 second on YouTube. It would be great if someone did something similar and try to explain inter-universal Teichmuller theory in 60 seconds…

May 27th, 2013

in IUTeich the theta function corresponds to the gaze of the little girl into the “small house”

Yesterday i was hoping for a 60 second introduction to inter-universal Teichmuller theory. Today i learned that Mochizuki himself provided such a thing.

Well, sort of…

In a one-page post he gives an ‘explanation’ of IUTeich via Sokkuri-Animation (Sokkuri being the Japanese for mirror-image). 

IUTeich, he says, should be viewed as a sequence of nested universes, which are represented by ‘houses’ in Sokkuri-Animation.
Galois groups and arithmetic fundamental groups behave as though they are made of a “mysterious substance” and in Sokkuri this “mysterious substance” corresponds to the “mysterious stars” that form the link between the “small” and “large” houses.
And, most importantly, the bridge between these nested universes corresponds to the gaze of the little girl into the “small house”…

Well, that explains everything, i think.

There’s a small image in the post but the link no longer works as the service stopped in january (via Google-translate).

A post at Hacker news identifies the image as coming from the YouTube linked below (2/4/2019 : link lost) and  discovers a connection to the paper titled ‘The ABC Conjecture and the Last Judgment by Giotto’ 

Yesterday i seriously doubted Ted Nelson’s claim that Mochizuki might be the anonymous Hatoshi Nakamoto, designer of BitCoin, having found little or no evidence of CypherPunk-parlance in Mochizuki’s papers…

Today, i’m not that certain any more.

May 28th, 2013

MochizukiDenial

Starting head-on with the 4 papers on inter-universal Teichmuller theory (IUTeich for the fans) is probably not the smartest move to enter Mochizuki-territory.

If you glanced through any of these papers or one of his numerous talks, you’ll know he makes a point of ‘extending’ or even ‘partially dismantling’  scheme theory using the new notion of Frobenioids, which should be some generalisation of Galois categories. 

So if you ever feel like wasting some months trying to figure out what his claimed proof of the ABC-conjecture is all about, a more advisable route might be to start with his two papers on ‘the geometry of Frobenioids’.

Lots of people must have tried that entrance before, and some even started a blog to record their progress as did the person (or persons) behind MochizukiDenial. Here’s the idea:

“Mochizuki deniers by contrast believe that the claim is not serious. They believe that the body of Mochizuki’s work contains neither a proof outline nor ideas powerful enough to resolve the ABC conjecture. We might be wrong. How do we propose to determine whether or not we are. In contrast to Mochizuki boosters on the internet, we will do this by determining what it is that Mochizuki’s papers purport to do. Stay tuned.”

Unfortunately, the project was given up after 2 days and three posts…

Today i tried to acquaint myself with the 126 pages of Frobenioids1 and have a splitting headache because i miss an extra 2Gb RAM to remember the 173 (or more) new concepts he introduces. 

May 29th, 2013

a baby Arithmetic Frobenioid

probably i should start-up a YouTube channel MinuteMochizuki but until i do here’s what i learned today: Alexei Bondal once told me that some Russians start a paper at the end and work their way to the front when needed. Sound advice when approaching M-papers!

So today i did start with the last section ‘Some Motivating Examples’ from Frobenioids1 and worked out what the simplest possible ArithmeticFrobenioid might be, that associated to the integers $\mathbb{Z}$.

Brace yourself here it comes. It is the category $\mathbf{C}$ with objects $(a)$ where $a$ is a strictly positive rational number and morphisms
$(a)\to (b)$ given by a couple $(n,c)$ where $n$ is a strictly positive integer and $c$ a strictly positive rational number subject to the condition that $a^n$ divides $c.b$ (meaning that the quotient is a strictly positive integer).

Cute (trivial) fact: compositions exist in the sense that
$$(m,d)\circ (n,c)=(n.m,c^m.d).$$
What makes $\mathbf{C}$ a frobenioid is that it comes with a functor $\mathbf{C}\to \mathbf{F}$ where $\mathbf{F}$ is the category with one object $\ast$ and morphisms elements of the noncommutative monoid consisting of all couples $(n,c)$ as before and multiplication as composition above, functor sending all $(a)$ to $\ast$ and morphisms to corresponding element of the monoid.

Mochizuki proves that we can recover $\mathbf{C}$ from the functor $\mathbf{C}\to \mathbf{F}$ (look at endomorphism-submonoids of the nc-monoid above) and that $\mathbf{C}$ contains enough info to reconstruct the scheme $\mathbf{Spec}(\mathbb{Z})$ from it (again, use the functor).

Next goal: bring in some Galois categories (tbc)…

May 31st, 2013

MinuteMochizuki 2 : a quadratic arithmetic Frobenioid

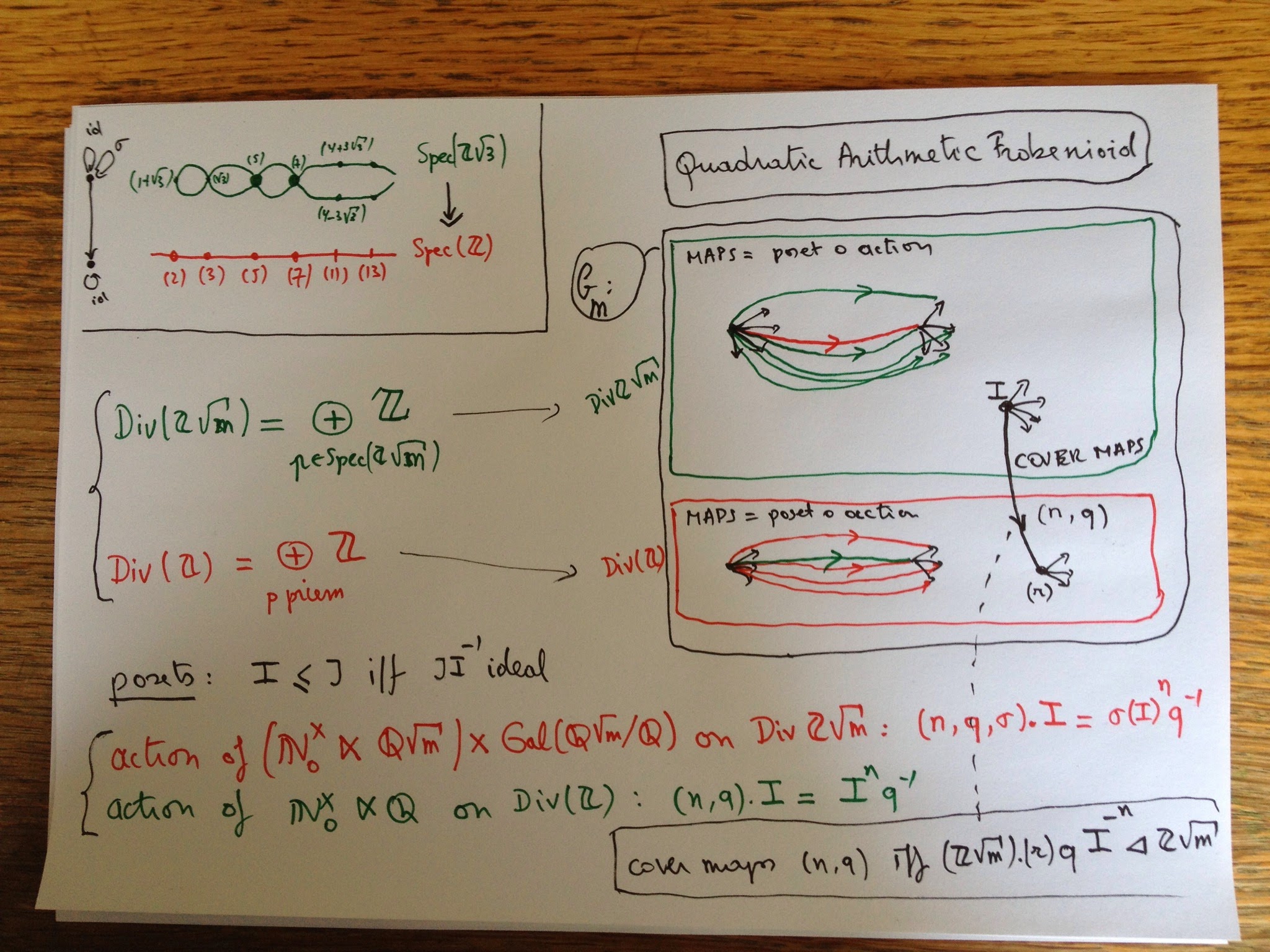
Let $m$ be a squarefree number not 1 mod 4 and say you want to recover the classical arithmetic scheme cover $\mathbf{Spec}(\mathbb{Z}[\sqrt{m}])$ onto $\mathbf{Spec}(\mathbb{Z})$ (top left hand corner for m=3).
Prime ideals of $\mathbb{Z}$ may remain prime in $\mathbb{Z}[\sqrt{m}]$ (e.g. (5) and (7)) or split into two prime ideals (e.g. (11)) or ramify (only (2) and (3)), all this governed by the Kronecker symbol.
If it remains prime then the quotient $\mathbb{Z}[\sqrt{m}]/(p)$ is the finite field on $p^2$ elements so has a non-trivial Frobenius morphism, which cannot be lifted to an auto of $\mathbb{Z}[\sqrt{m}]$ to cannot be expressed in scheme language.

For this reason (i think) Mochizuki introduced Frobenioids which are categories allowing one to recover the classical scheme cover but also containing info on the power maps $x\to x^n$ for all $n$.

In the quadratic case, the objects of the Frobenioid for $\mathbb{Z}[\sqrt{m}]$ is the union of all fractional ideals (that is submodules of $\mathbb{Q}(\sqrt{m})$ of the form $I.q$ where $I$ is an ideal and $q$ non-zero in $\mathbb{Q}(\sqrt{m}))$ and all fractional ideals of $\mathbb{Z}$ (similar defined). Dedekind already knew they correspond to elements of the free Abelian groups on the set of prime ideals and hence have a natural poset-structure.

Now, there are monoid actions on these two posets, giving another set of arrows (for fractional ideals of $\mathbb{Z}[\sqrt{m}]$ the black arrows indicate the poset and the red arrow is the action. Now, the morphisms in the Frobenioid $\mathbf{C}(m)$ are all compositions of an action arrow followed by a poset-arrow (the green ones in the $\mathbb{Z}[\sqrt{m}]$ part, the red ones in the $\mathbb{Z}$-part. Then there is a third set of arrows encoding the Galois-covering info (the black arrows between the two parts). Again, one verifies that compositions exist.

A very special case of Mochizuki’s first Frobenioid paper is that $\mathbf{C}(m)$ contains enough info to recover the scheme cover and even the quadratic field $\mathbb{Q}(\sqrt{m})$. That is, if $\mathbf{C}(m)$ is equivalent to another such one $\mathbf{C}(m^{\prime })$ then $m=m^{\prime }$. Also note that $\mathbf{C}(m)$ contains info on all power maps, so we have somehow ‘lifted’ the Frobenius-maps from the quotients to $\mathbb{Z}[\sqrt{m}]$ at the expense of ‘partially dismantling scheme theory’ (M’s words).

Another neat fact about $\mathbf{C}(m)$ is that all arrows are epimorphisms (compare this to groupoids where all morphisms are isomorphisms). Of course, this only becomes important for more complicated Galois-settings, ideally for the algebraic closure of $\mathbb{Q}$.

June 1st, 2013

Should I stay or should I blog now?

+Alex Nelson commented on +John Baez reshare of my last post on Mochizuki’s Frobenioids:
 
“I just wish he’d blog these, to make it a wee bit easier to read…and print out…”

Valid point, so i did spend some time to make blog-versions of my two G+ posts on this, the last one is linked below, the first one is here (2/4/2019 : lost post).

I’m not sure whether i should continue with this cross-posting. I kinda liked the quick-and-dirty approach of instant-uploading snaps-shots of doodles here. Writing a blogpost  takes more time.

Let me know if it does make a difference to you.

June 3rd, 2013

Mochizuki’s menagerie of morphisms

After zillions of definitions, Mochizuki almost shows empathy with the reader (on page 26 of Frobenioids1) and remarks  that it may be useful to draw a “Chart of Types of Morphisms in a Frobenioid”  (and does this on page 124).

Extremely useful indeed. Try to figure out what a morphism of Frobenius-type might be. It starts like this: it is an LB-invertible base-isomorphism. An LB-invertible map itself is a co-angular and isometric map. A co-angular map itself is defined by the property that for any factorization aoboc of it, where a is linear, b is an isometric pre-step and either a or c are base-isomorphisms, it follows that b is an isomorphism. A pre-step itself is …. etc.etc.

Today i tried to work out what all this means in the case of an arithmetic Frobenioid. Recall that this is a category with objects the elements of layers of posets, each layer (meant to represent the ‘dismantled’ prime-spectrum of a ring of integers $R$ in a number field $K$) the set of fractional ideals in the number field. In each layer we have operations of three types

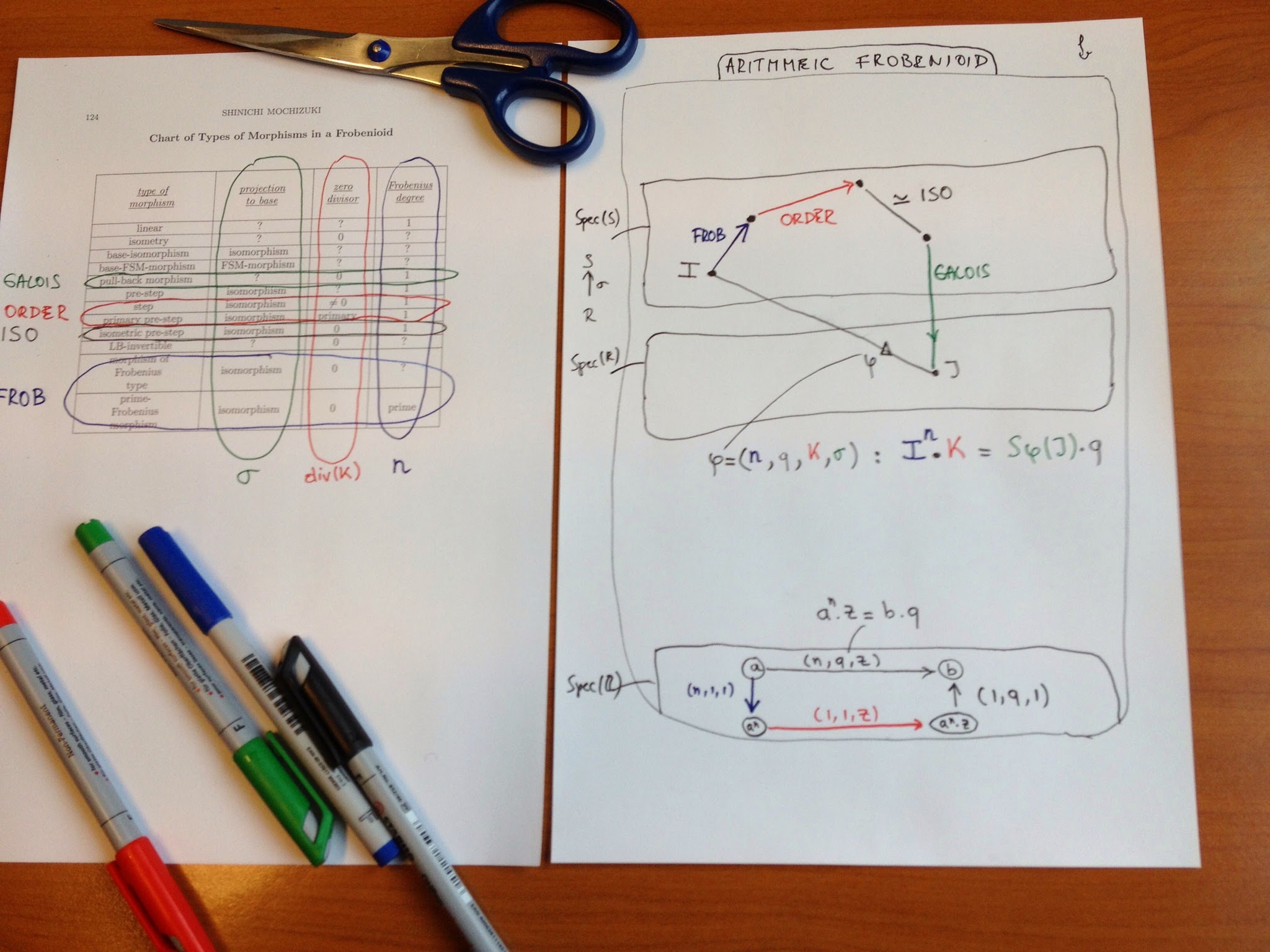
– Frobenius-type : sending a fractional ideal $I$ to an n-th power $I^n$ (the blue morphisms)
– Poset-type : given by multiplying $I$ with an ideal $K$ of $R$ (the red morphisms, the ‘steps’ in M-parlance)
– Isomorphisms (the blacks, ‘isometric pre-steps’ according to M) which are either isos of fractional ideals (given by multiplying with a non-zero element $q$ of $K$) or Galois action maps on fractional ideals.

The relevant operation between different layers is that of extension of fractional ideals. So, let $\sigma :R\to S$ be a ring-map induced by a field-iso on $L$, the number-field of $S$, then this operation sends a fractional ideal $J$ in $K$ to the extended fractional ideal $S.\sigma (J)$ in $L$.

What Mochizuki shows is that any arrow in the arithmetic Frobenioid has an essentially unique factorisation into these four types of morphisms (essentially meaning unto irrelevant  isos trown in at one place and compensated by the inverse at the next place).

Let’s work this out for the baby arithmetic Frobenioid corresponding to the integers.

Objects correspond to strictly positive rational numbers $a$, and morphisms are of the form $\varphi =(n,q,z):a\to b$  where $n$ and $z$ are strictly positive integers and $q$ a strictly positive rational number satisfying $a^n.z=b.q$.

This map can then be factored as a Frobenius-type map $(n,1,1)$ sending $a$ to $a^n$, followed by a poset-map $(1,1,z)$ sending $a^n$ to $a^n.z$ followed by an isomorphism $(1,q^{-1},1)$ sending $a^n.z$ to $a^n.z.q^{-1}=b$.

These different types of morphisms will become important when we want to reconstruct the arithmetic schemes (and covers) from the category structure of the Frobenioid. The essential trick will be to classify and distinguish the irreducible morphisms which are non-isomorphisms phi such that in any factorisation $\varphi =\alpha \circ \beta$, either $\alpha$ or $\beta$ must be an isomorphism. (tbc)