PseudonomousDaughterTwo learned vector-addition at school and
important formulas such as the _Chasles-Moebius_ equation
$\forall A,B,C \in \mathbb{R}^2~:~\vec{AB}+\vec{BC} = \vec{AC} $
Last evening I helped her a bit with her homework and there was one
problem she could not do immediately (but it was a starred exercise so
you didn't have to do it, but…) :
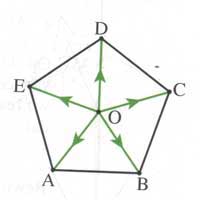
consider a regular pentagon
with center $\vec{0} $. Prove that
$\vec{0A} + \vec{0B} +
\vec{0C} + \vec{0D} + \vec{0E} = \vec{0} $
PD2 : How would
_you_ do this? (with a tone like : I bet even you can't do
it)
Me : Symmetry!
PD2 : Huh?
Me : Rotate the plane
1/5 turn, then $A \mapsto B $, $B \mapsto C $ and so on. So the vector
giving the sum of all five terms must be mapped to itself under this
rotation and the only vector doing this is the zero vector.
PD2 :
That cannot be the solution, you didn't take sums of vectors and all
other exercises did that.
Me : I don't care, it is an elegant
solution, you don't have to compute a thing!
But clearly
she was not convinced and I had to admit there was nothing in her
textbook preparing her for such an argument. I was about to explain that
there was even more symmetry : reflecting along a line through a vertex
giving dihedral symmetry when I saw what the _intended solution_
of the exercise was :
Me : Okay, if you _have_ to do
sums let us try this. Fix a vertex, say A. Then the sum
$\vec{0E}+\vec{0B} $ must lie on the line 0A by the parallellogram-rule
(always good to drop in a word from the textbook to gain some
trust…), similarly the sum $\vec{0C}+\vec{0D} $ must lie on the
line 0A. So you now have to do a sum of three vectors lying on the
line 0A so the result must lie on 0A
PD2 : Yes, and???
Me : But there was nothing special about $A$. I could have started with
B and do the whole argument all over again and then I would get that
the sum is a vector on the line 0B
PD2 : And the only vector
lying on both 0A and 0B is $\vec{0} $
Me : Right! But
all we did now was just redoing the symmetry argument because the line
0A is mapped to 0B
PD2 : Don't you get started on
_that symmetry_ again!
I wonder which of the two
solutions she will sell today as her own. I would love to see the face
of a teacher when a 15yr old says “Clearly that is trivial because
the zero vector is the only one left invariant under
pentagon-symmetry!”
Comments