Last
time we saw that the _coalgebra of distributions_ of a
noncommutative manifold can be described as a coalgebra
Takeuchi-equivalent to the path coalgebra of a huge quiver. This
infinite quiver has as its vertices the isomorphism classes of finite
dimensional simple representations of the qurve A (the coordinate ring
of the noncommutative manifold) and there are as many directed arrows
between the vertices corresponding to the simples S and T as is the
dimension of $Ext^1_A(S,T) $.
The fact that this
coalgebra of distributions is equivalent to the path coalgebra of
_some_ quiver is in the Kontsevich-Soibelman
paper though it would have been nice if they had given reference for
this fact to the paper Wedge Products and
Cotensor Coalgebras in Monoidal Categories by Ardizzoni or to
previous work by P. Jara, D. Llena, L. Merino and D. Stefan,
“Hereditary and formally smooth coalgebras”, Algebr.
Represent. Theory 8 (2005), 363-374. In those papers it is shown that a
coalgebra with coseparable coradical is hereditary if and only if it
is formally smooth if and only if it is a cotensor coalgebra of some
bicomodule.
At first this looks just like the dual version of
the classical result that a finite dimensional hereditary algebra is
Morita equivalent to the path algebra of a quiver (which is indeed what
the proof does) but again the condition that the coradical is
coseparable does not require the coradical to be finite dimensional…
In our case, the coradical is indeed coseparable being the direct sum
over all matrix coalgebras corresponding to the simple representations.
Hence, we can again recover the _points_ of our noncommutative manifold
from the direct summands of the coradical. Fortunately, one can
compute this huge coalgebra of distributions from a small quiver, the
_one quiver to rule them all_, but as I’ve been babbling about all of
this here [numerous
times](https://lievenlb.local/?s=one+quiver) I’ll let the
interested find out for themselves how you use it (a) to get at the
isoclasses of all simples (hint : morally they are the smooth points of
the quotient varieties of n-dimensional representations and enough tools
have been developed recently to spot some fake simples, that is smooth
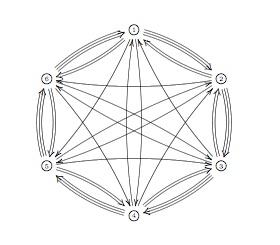
proper semi-simple points) and (b) to compute the _ragball_, that is the
huge quiver with vertex set the simples and arows as described
above. Over the years I’ve calculated several one-quivers for a
variety of qurves (such as amalgamated free products of finite groups
and smooth curves). If you are in for a puzzle, try to determine it for
the qurve $~(\mathbb{C}[x] \ast C_2) \ast_{\mathbb{C}
C_2} \mathbb{C} PSL_2(\mathbb{Z}) \ast_{\mathbb{C} C_3}
(\mathbb{C}[x] \ast C_3) $ The answer is a mysterious
hexagon
Comments