Category: stories

So, who did discover the Leech lattice?

Published December 20, 2010 by lieven

For the better part of the 30ties, Ernst Witt (1) did hang out with the rest of the ‘Noetherknaben’, the group of young mathematicians around Emmy Noether (3) in Gottingen.

In 1934 Witt became Helmut Hasse‘s assistent in Gottingen, where he qualified as a university lecturer in 1936. By 1938 he has made enough of a name for himself to be offered a lecturer position in Hamburg and soon became an associate professor, the down-graded position held by Emil Artin (2) until he was forced to emigrate in 1937.

A former fellow student of him in Gottingen, Erna Bannow (4), had gone earlier to Hamburg to work with Artin. She continued her studies with Witt and finished her Ph.D. in 1939. In 1940 Erna Bannow and Witt married.

So, life was smiling on Ernst Witt that sunday january 28th 1940, both professionally and personally. There was just one cloud on the horizon, and a rather menacing one. He was called up by the Wehrmacht and knew he had to enter service in february. For all he knew, he was spending the last week-end with his future wife… (later in february 1940, Blaschke helped him to defer his military service by one year).

Still, he desperately wanted to finish his paper before entering the army, so he spend most of that week-end going through the final version and submitted it on monday, as the published paper shows.

In the 70ties, Witt suddenly claimed he did discover the Leech lattice $ {\Lambda} $ that sunday. Last time we have seen that the only written evidence for Witt’s claim is one sentence in his 1941-paper Eine Identität zwischen Modulformen zweiten Grades. “Bei dem Versuch, eine Form aus einer solchen Klassen wirklich anzugeben, fand ich mehr als 10 verschiedene Klassen in $ {\Gamma_{24}} $.”

But then, why didn’t Witt include more details of this sensational lattice in his paper?

Ina Kersten recalls on page 328 of Witt’s collected papers : “In his colloquium talk “Gitter und Mathieu-Gruppen” in Hamburg on January 27, 1970, Witt said that in 1938, he had found nine lattices in $ {\Gamma_{24}} $ and that later on January 28, 1940, while studying the Steiner system $ {S(5,8,24)} $, he had found two additional lattices $ {M} $ and $ {\Lambda} $ in $ {\Gamma_{24}} $. He continued saying that he had then given up the tedious investigation of $ {\Gamma_{24}} $ because of the surprisingly low contribution

$ \displaystyle | Aut(\Lambda) |^{-1} < 10^{-18} $

to the Minkowski density and that he had consented himself with a short note on page 324 in his 1941 paper.”

In the last sentence he refers to the fact that the sum of the inverse orders of the automorphism groups of all even unimodular lattices of a given dimension is a fixed rational number, the Minkowski-Siegel mass constant. In dimension 24 this constant is

$ \displaystyle \sum_{L} \frac{1}{| Aut(L) |} = \frac {1027637932586061520960267}{129477933340026851560636148613120000000} \approx 7.937 \times 10^{-15} $

That is, Witt was disappointed by the low contribution of the Leech lattice to the total constant and concluded that there might be thousands of new even 24-dimensional unimodular lattices out there, and dropped the problem.

If true, the story gets even better : not only claims Witt to have found the lattices $ {A_1^{24}=M} $ and $ {\Lambda} $, but also enough information on the Leech lattice in order to compute the order of its automorphism group $ {Aut(\Lambda)} $, aka the Conway group $ {Co_0 = .0} $ the dotto-group!

Is this possible? Well fortunately, the difficulties one encounters when trying to compute the order of the automorphism group of the Leech lattice from scratch, is one of the better documented mathematical stories around.

The books From Error-Correcting Codes through Sphere Packings to Simple Groups by Thomas Thompson, Symmetry and the monster by Mark Ronan, and Finding moonshine by Marcus du Sautoy tell the story in minute detail.

It took John Conway 12 hours on a 1968 saturday in Cambridge to compute the order of the dotto group, using the knowledge of Leech and McKay on the properties of the Leech lattice and with considerable help offered by John Thompson via telephone.

But then, John Conway is one of the fastest mathematicians the world has known. The prologue of his book On numbers and games begins with : “Just over a quarter of a century ago, for seven consecutive days I sat down and typed from 8:30 am until midnight, with just an hour for lunch, and ever since have described this book as “having been written in a week”.”

Conway may have written a book in one week, Ernst Witt did complete his entire Ph.D. in just one week! In a letter of August 1933, his sister told her parents : “He did not have a thesis topic until July 1, and the thesis was to be submitted by July 7. He did not want to have a topic assigned to him, and when he finally had the idea, he started working day and night, and eventually managed to finish in time.”

So, if someone might have beaten John Conway in fast-computing the dottos order, it may very well have been Witt. Sadly enough, there is a lot of circumstantial evidence to make Witt’s claim highly unlikely.

For starters, psychology. Would you spend your last week-end together with your wife to be before going to war performing an horrendous calculation?

Secondly, mathematical breakthroughs often arise from newly found insight. At that time, Witt was also working on his paper on root lattices “Spiegelungsgrupen and Aufzähling halbeinfacher Liescher Ringe” which he eventually submitted in january 1941. Contained in that paper is what we know as Witt’s lemma which tells us that for any integral lattice the sublattice generated by vectors of norms 1 and 2 is a direct sum of root lattices.

This leads to the trick of trying to construct unimodular lattices by starting with a direct sum of root lattices and ‘adding glue’. Although this gluing-method was introduced by Kneser as late as 1967, Witt must have been aware of it as his 16-dimensional lattice $ {D_{16}^+} $ is constructed this way.

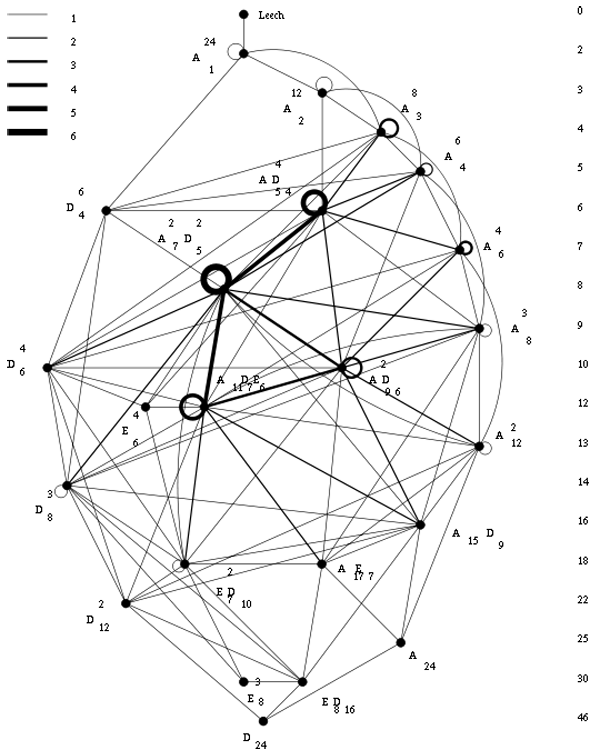
If Witt wanted to construct new 24-dimensional even unimodular lattices in 1940, it would be natural for him to start off with direct sums of root lattices and trying to add vectors to them until he got what he was after. Now, all of the Niemeier-lattices are constructed this way, except for the Leech lattice!

I’m far from an expert on the Niemeier lattices but I would say that Witt definitely knew of the existence of $ {D_{24}^+} $, $ {E_8^3} $ and $ {A_{24}^+} $ and that it is quite likely he also constructed $ {(D_{16}E_8)^+, (D_{12}^2)^+, (A_{12}^2)^+, (D_8^3)^+} $ and possibly $ {(A_{17}E_7)^+} $ and $ {(A_{15}D_9)^+} $. I’d rate it far more likely Witt constructed another two such lattices on sunday january 28th 1940, rather than discovering the Leech lattice.

Finally, wouldn’t it be natural for him to include a remark, in his 1941 paper on root lattices, that not every even unimodular lattices can be obtained from sums of root lattices by adding glue, the Leech lattice being the minimal counter-example?

If it is true he was playing around with the Steiner systems that sunday, it would still be a pretty good story he discovered the lattices $ {(A_2^{12})^+} $ and $ {(A_1^{24})^+} $, for this would mean he discovered the Golay codes in the process!

Which brings us to our next question : who discovered the Golay code?

Comments closed

Who discovered the Leech lattice?

Published November 30, 2010 by lieven

The Leech lattice was, according to wikipedia, ‘originally discovered by Ernst Witt in 1940, but he did not publish his discovery’ and it ‘was later re-discovered in 1965 by John Leech’. However, there is very little evidence to support this claim.

The facts

What is certain is that John Leech discovered in 1965 an amazingly dense 24-dimensional lattice $ {\Lambda} $ having the property that unit balls around the lattice points touch, each one of them having exactly 196560 neighbors. The paper ‘Notes on sphere packings’ appeared in 1967 in the Canad. J. Math. 19, 251-267.

Compare this to the optimal method to place pennies on a table, leading to the hexagonal tiling, each penny touching exactly 6 others. Similarly, in dimension 8 the densest packing is the E8 lattice in which every unit ball has exactly 240 neighbors.

The Leech lattice $ {\Lambda} $ can be characterized as the unique unimodular positive definite even lattice such that the length of any non-zero vector is at least two.

The list of all positive definite even unimodular lattices, $ {\Gamma_{24}} $, in dimension 24 was classified later by Hans-Volker Niemeier and are now known as the 24 Niemeier lattices.

For the chronology below it is perhaps useful to note that, whereas Niemeier’s paper did appear in 1973, it was submitted april 5th 1971 and is just a minor rewrite of Niemeier’s Ph.D. “Definite quadratische Formen der Dimension 24 und Diskriminante 1” obtained in 1968 from the University of Göttingen with advisor Martin Kneser.

The claim

On page 328 of Ernst Witt’s Collected Papers Ina Kersten recalls that Witt gave a colloquium talk on January 27, 1970 in Hamburg entitled “Gitter und Mathieu-Gruppen” (Lattices and Mathieu-groups). In this talk Witt claimed to have found nine lattices in $ {\Gamma_{24}} $ as far back as 1938 and that on January 28, 1940 he found two additional lattices $ {M} $ and $ {\Lambda} $ while studying the Steiner system $ {S(5,8,24)} $.

On page 329 of the collected papers is a scan of the abstract Witt wrote in the colloquium book in Bielefeld where he gave a talk “Uber einige unimodularen Gitter” (On certain unimodular lattices) on January 28, 1972

Here, Witt claims that he found three new lattices in $ {\Gamma_{24}} $ on January 28, 1940 as the lattices $ {M} $, $ {M’} $ and $ {\Lambda} $ ‘feiern heute ihren 32sten Gebursttag!’ (celebrate today their 32nd birthday).

He goes on telling that the lattices $ {M} $ and $ {\Lambda} $ were number 10 and 11 in his list of lattices in $ {\Gamma_{24}} $ in his paper “Eine Identität zwischen Modulformen zweiten Grades” in the Abh. Math. Sem. Univ. Hamburg 14 (1941) 323-337 and he refers in particular to page 324 of that paper.

He further claims that he computed the orders of their automorphism groups and writes that $ {\Lambda} $ ‘wurde 1967 von Leech wieder-entdeckt’ (was re-discovered by Leech in 1967) and that its automorphism group $ {G(\Lambda)} $ was studied by John Conway. Recall that Conway’s investigations of the automorphism group of the Leech lattice led to the discovery of three new sporadic groups, the Conway groups $ {Co_1,Co_2} $ and $ {Co_3} $.

However, Witt’s 1941-paper does not contain a numbered list of 24-dimensional lattices. In fact, apart from $ {E_8+E_8+E_8} $ is does not contain a single lattice in $ {\Gamma_{24}} $. The only relevant paragraph is indeed on page 324

He observes that Mordell already proved that there is just one lattice in $ {\Gamma_8} $ (the $ {E_8} $-lattice) and that the main result of his paper is to prove that there are precisely two even unimodular 16-dimensional lattices : $ {E_8+E_8} $ and another lattice, now usually called the 16-dimensional Witt-lattice.

He then goes on to observe that Schoeneberg knew that $ {\# \Gamma_{24} > 1} $ and so there must be more lattices than $ {E_8+E_8+E_8} $ in $ {\Gamma_{24}} $. Witt concludes with : “In my attempt to find such a lattice, I discovered more than 10 lattices in $ {\Gamma_{24}} $. The determination of $ {\# \Gamma_{24}} $ does not seem to be entirely trivial.”

Hence, it is fair to assume that by 1940 Ernst Witt had discovered at least 11 of the 24 Niemeier lattices. Whether the Leech lattice was indeed lattice 11 on the list is anybody’s guess.

Next time we will look more closely into the historical context of Witt’s 1941 paper.

One Comment

math & manic-depression, a Faustian bargain

Published July 15, 2010 by lieven

In the wake of a colleague’s suicide and the suicide of three students, Matilde Marcolli gave an interesting and courageous talk at Caltech in April : The dark heart of our brightness: bipolar disorder and scientific creativity. Although these slides give a pretty good picture of the talk, if you can please take the time to watch it (the talk starts 44 minutes into the video).

Courageous because as the talk progresses, she gives more and more examples from her own experiences, thereby breaking the taboo surrounding the topic of bipolar mood disorder among scientists. Interesting because she raises a couple of valid points, well worth repeating.

We ~~didn’t~~ can see it coming

We are always baffled when someone we know commits suicide, especially if that person is extremely successful in his/her work. ‘(S)he was so full of activity!’, ‘We did not see it coming!’ etc. etc.

Matilde argues that if a person suffers from bipolar mood disorder (from mild forms to full-blown manic-depression), a condition quite common among scientists and certainly mathematicians, we can see it coming, if we look for the proper signals!

We, active scientists, are pretty good at hiding a down-period. We have collected an arsenal of tricks not to send off signals when we feel depressed, simply because it’s not considered cool behavior. On the other hand, in our manic phases, we are quite transparent because we like to show off our activity and creativity!

Matilde tells us to watch out for people behaving orders-of-magnitude out of their normal-mode behavior. Say, someone who normally posts one or two papers a year on the arXiv, suddenly posting 5 papers in one month. Or, someone going rarely to a conference, now spending a summer flying from one conference to the next. Or, someone not blogging for months, suddenly flooding you with new posts…

As scientists we are good at spotting such order-of-magnitude-out-behavior. So we can detect friends and colleagues going through a manic-phase and hence should always take such a person serious (and try to offer help) when they send out signals of distress.

Mood disorder, a Faustian bargain

The Faust legend :
“Despite his scholarly eminence, Faust is bored and disappointed. He decides to call on the Devil for further knowledge and magic powers with which to indulge all the pleasures of the world. In response, the Devil’s representative Mephistopheles appears. He makes a bargain with Faust: Mephistopheles will serve Faust with his magic powers for a term of years, but at the end of the term, the Devil will claim Faust’s soul and Faust will be eternally damned.”

Mathematicians suffering from mood disorder seldom see their condition as a menace, but rather as an advantage. They know they do their best and most creative work in short spells of intense activity during their manic phase and take the down-phase merely as a side effect. We fear that if we seek treatment, we may as well loose our creativity.

That is, like Faust, we indulge the pleasures of our magic powers during a manic-phase, knowing only too well that the devilish depression-phase may one day claim our life or mental sanity…

Comments closed