Category: number theory

Langlands versus Connes

Published October 26, 2010 by lieven

This is a belated response to a Math-Overflow exchange between Thomas Riepe and Chandan Singh Dalawat asking for a possible connection between Connes’ noncommutative geometry approach to the Riemann hypothesis and the Langlands program.

Here’s the punchline : a large chunk of the Connes-Marcolli book Noncommutative Geometry, Quantum Fields and Motives can be read as an exploration of the noncommutative boundary to the Langlands program (at least for $GL_1 $ and $GL_2 $ over the rationals $\mathbb{Q} $).

Recall that Langlands for $GL_1 $ over the rationals is the correspondence, given by the Artin reciprocity law, between on the one hand the abelianized absolute Galois group

$Gal(\overline{\mathbb{Q}}/\mathbb{Q})^{ab} = Gal(\mathbb{Q}(\mu_{\infty})/\mathbb{Q}) \simeq \hat{\mathbb{Z}}^* $

and on the other hand the connected components of the idele classes

$\mathbb{A}^{\ast}_{\mathbb{Q}}/\mathbb{Q}^{\ast} = \mathbb{R}^{\ast}_{+} \times \hat{\mathbb{Z}}^{\ast} $

The locally compact Abelian group of idele classes can be viewed as the nice locus of the horrible quotient space of adele classes $\mathbb{A}_{\mathbb{Q}}/\mathbb{Q}^{\ast} $. There is a well-defined map

$\mathbb{A}_{\mathbb{Q}}’/\mathbb{Q}^{\ast} \rightarrow \mathbb{R}_{+} \qquad (x_{\infty},x_2,x_3,\ldots) \mapsto | x_{\infty} | \prod | x_p |_p $

from the subset $\mathbb{A}_{\mathbb{Q}}’ $ consisting of adeles of which almost all terms belong to $\mathbb{Z}_p^{\ast} $. The inverse image of this map over $\mathbb{R}_+^{\ast} $ are precisely the idele classes $\mathbb{A}^{\ast}_{\mathbb{Q}}/\mathbb{Q}^{\ast} $. In this way one can view the adele classes as a closure, or ‘compactification’, of the idele classes.

This is somewhat reminiscent of extending the nice action of the modular group on the upper-half plane to its badly behaved action on the boundary as in the Manin-Marcolli cave post.

The topological properties of the fiber over zero, and indeed of the total space of adele classes, are horrible in the sense that the discrete group $\mathbb{Q}^* $ acts ergodically on it, due to the irrationality of $log(p_1)/log(p_2) $ for primes $p_i $. All this is explained well (in the semi-local case, that is using $\mathbb{A}_Q’ $ above) in the Connes-Marcolli book (section 2.7).

In much the same spirit as non-free actions of reductive groups on algebraic varieties are best handled using stacks, such ergodic actions are best handled by the tools of noncommutative geometry. That is, one tries to get at the geometry of $\mathbb{A}_{\mathbb{Q}}/\mathbb{Q}^{\ast} $ by studying an associated non-commutative algebra, the skew-ring extension of the group-ring of the adeles by the action of $\mathbb{Q}^* $ on it. This algebra is known to be Morita equivalent to the Bost-Connes algebra which is the algebra featuring in Connes’ approach to the Riemann hypothesis.

It shouldn’t thus come as a major surprise that one is able to recover the other side of the Langlands correspondence, that is the Galois group $Gal(\mathbb{Q}(\mu_{\infty})/\mathbb{Q}) $, from the Bost-Connes algebra as the symmetries of certain states.

In a similar vein one can read the Connes-Marcolli $GL_2 $-system (section 3.7 of their book) as an exploration of the noncommutative closure of the Langlands-space $GL_2(\mathbb{A}_{\mathbb{Q}})/GL_2(\mathbb{Q}) $.

At the moment I’m running a master-seminar noncommutative geometry trying to explain this connection in detail. But, we’re still in the early phases, struggling with the topology of ideles and adeles, reciprocity laws, L-functions and the lot. Still, if someone is interested I might attempt to post some lecture notes here.

Comments closed

Lambda-rings for formula-phobics

Published February 5, 2010 by lieven

In 1956, Alexander Grothendieck (middle) introduced $\lambda $-rings in an algebraic-geometric context to be commutative rings A equipped with a bunch of operations $\lambda^i $ (for all numbers $i \in \mathbb{N}_+ $) satisfying a list of rather obscure identities. From the easier ones, such as

$\lambda^0(x)=1, \lambda^1(x)=x, \lambda^n(x+y) = \sum_i \lambda^i(x) \lambda^{n-i}(y) $

to those expressing $\lambda^n(x.y) $ and $\lambda^m(\lambda^n(x)) $ via specific universal polynomials. An attempt to capture the essence of $\lambda $-rings without formulas?

Lenstra’s elegant construction of the 1-power series rings $~(\Lambda(A),\oplus,\otimes) $ requires only one identity to remember

$~(1-at)^{-1} \otimes (1-bt)^{-1} = (1-abt)^{-1} $.

Still, one can use it to show the existence of ringmorphisms $\gamma_n~:~\Lambda(A) \rightarrow A $, for all numbers $n \in \mathbb{N}_+ $. Consider the formal ‘logarithmic derivative’

$\gamma = \frac{t u(t)’}{u(t)} = \sum_{i=1}^\infty \gamma_i(u(t))t^i~:~\Lambda(A) \rightarrow A[[t]] $

where $u(t)’ $ is the usual formal derivative of a power series. As this derivative satisfies the chain rule, we have

$\gamma(u(t) \oplus v(t)) = \frac{t (u(t)v(t))’}{u(t)v(t)} = \frac{t(u(t)’v(t)+u(t)v(t)’}{u(t)v(t))} = \frac{tu(t)’}{u(t)} + \frac{tv(t)’}{v(t)} = \gamma(u(t)) + \gamma(v(t)) $

and so all the maps $\gamma_n~:~\Lambda(A) \rightarrow A $ are additive. To show that they are also multiplicative, it suffices by functoriality to verify this on the special 1-series $~(1-at)^{-1} $ for all $a \in A $. But,

$\gamma((1-at)^{-1}) = \frac{t \frac{a}{(1-at)^2}}{(1-at)} = \frac{at}{(1-at)} = at + a^2t^2 + a^3t^3+\ldots $

That is, $\gamma_n((1-at)^{-1}) = a^n $ and Lenstra’s identity implies that $\gamma_n $ is indeed multiplicative! A first attempt :

hassle-free definition 1 : a commutative ring $A $ is a $\lambda $-ring if and only if there is a ringmorphism $s_A~:~A \rightarrow \Lambda(A) $ splitting $\gamma_1 $, that is, such that $\gamma_1 \circ s_A = id_A $.

In particular, a $\lambda $-ring comes equipped with a multiplicative set of ring-endomorphisms $s_n = \gamma_n \circ s_A~:~A \rightarrow A $ satisfying $s_m \circ s_m = s_{mn} $. One can then define a $\lambda $-ringmorphism to be a ringmorphism commuting with these endo-morphisms.

The motivation being that $\lambda $-rings are known to form a subcategory of commutative rings for which the 1-power series functor is the right adjoint to the functor forgetting the $\lambda $-structure. In particular, if $A $ is a $\lambda $-ring, we have a ringmorphism $A \rightarrow \Lambda(A) $ corresponding to the identity morphism.

But then, what is the connection to the usual one involving all the operations $\lambda^i $? Well, one ought to recover those from $s_A(a) = (1-\lambda^1(a)t+\lambda^2(a)t^2-\lambda^3(a)t^3+…)^{-1} $.

For $s_A $ to be a ringmorphism will require identities among the $\lambda^i $. I hope an expert will correct me on this one, but I’d guess we won’t yet obtain all identities required. By the very definition of an adjoint we must have that $s_A $ is a morphism of $\lambda $-rings, and, this would require defining a $\lambda $-ring structure on $\Lambda(A) $, that is a ringmorphism $s_{AH}~:~\Lambda(A) \rightarrow \Lambda(\Lambda(A)) $, the so called Artin-Hasse exponential, to which I’d like to return later.

For now, we can define a multiplicative set of ring-endomorphisms $f_n~:~\Lambda(A) \rightarrow \Lambda(A) $ from requiring that $f_n((1-at)^{-1}) = (1-a^nt)^{-1} $ for all $a \in A $. Another try?

hassle-free definition 2 : $A $ is a $\lambda $-ring if and only if there is splitting $s_A $ to $\gamma_1 $ satisfying the compatibility relations $f_n \circ s_A = s_A \circ s_n $.

But even then, checking that a map $s_A~:~A \rightarrow \Lambda(A) $ is a ringmorphism is as hard as verifying the lists of identities among the $\lambda^i $. Fortunately, we get such a ringmorphism for free in the important case when A is of ‘characteristic zero’, that is, has no additive torsion. Then, a ringmorphism $A \rightarrow \Lambda(A) $ exists whenever we have a multiplicative set of ring endomorphisms $F_n~:~A \rightarrow A $ for all $n \in \mathbb{N}_+ $ such that for every prime number $p $ the morphism $F_p $ is a lift of the Frobenius, that is, $F_p(a) \in a^p + pA $.

Perhaps this captures the essence of $\lambda $-rings best (without the risk of getting an headache) : in characteristic zero, they are the (commutative) rings having a multiplicative set of endomorphisms, generated by lifts of the Frobenius maps.

Comments closed

Seating the first few thousand Knights

Published February 3, 2010 by lieven

The Knight-seating problems asks for a consistent placing of n-th Knight at an odd root of unity, compatible with the two different realizations of the algebraic closure of the field with two elements.
The first identifies the multiplicative group of its non-zero elements with the group of all odd complex roots of unity, under complex multiplication. The second uses Conway’s ‘simplicity rules’ to define an addition and multiplication on the set of all ordinal numbers.

The odd Knights of the round table-problem asks for a specific one-to-one correspondence between two realizations of ‘the’ algebraic closure $\overline{\mathbb{F}_2} $ of the field of two elements.

The first identifies the multiplicative group of its non-zero elements with the group of all odd complex roots of unity, under complex multiplication. The addition on $\overline{\mathbb{F}_2} $ is then recovered by inducing an involution on the odd roots, pairing the one corresponding to x to the one corresponding to x+1.

The second uses Conway’s ‘simplicity rules’ to define an addition and multiplication on the set of all ordinal numbers. Conway proves in ONAG that this becomes an algebraically closed field of characteristic two and that $\overline{\mathbb{F}_2} $ is the subfield of all ordinals smaller than $\omega^{\omega^{\omega}} $. The finite ordinals (the natural numbers) form the quadratic closure of $\mathbb{F}_2 $.

On the natural numbers the Conway-addition is binary addition without carrying and Conway-multiplication is defined by the properties that two different Fermat-powers $N=2^{2^i} $ multiply as they do in the natural numbers, and, Fermat-powers square to its sesquimultiple, that is $N^2=\frac{3}{2}N $. Moreover, all natural numbers smaller than $N=2^{2^{i}} $ form a finite field $\mathbb{F}_{2^{2^i}} $. Using distributivity, one can write down a multiplication table for all 2-powers.

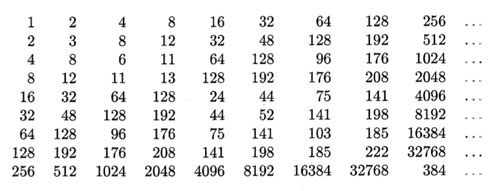
The Knight-seating problems asks for a consistent placing of n-th Knight $K_n $ at an odd root of unity, compatible with the two different realizations of $\overline{\mathbb{F}_2} $. Last time, we were able to place the first 15 Knights as below, and asked where you would seat $K_{16} $

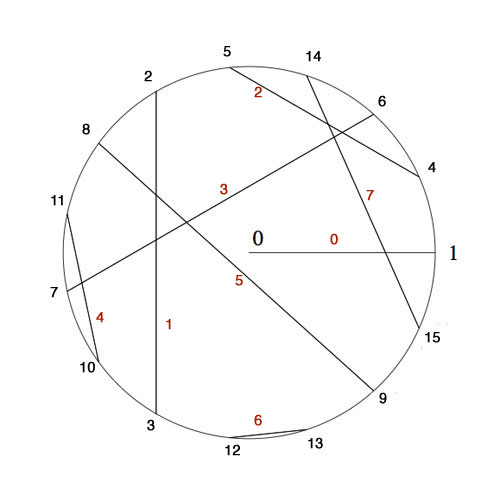
$K_4 $ was placed at $e^{2\pi i/15} $ as 4 was the smallest number generating the ‘Fermat’-field $\mathbb{F}_{2^{2^2}} $ (with multiplicative group of order 15) subject to the compatibility relation with the generator 2 of the smaller Fermat-field $\mathbb{F}_2 $ (with group of order 15) that $4^5=2 $.

To include the next Fermat-field $\mathbb{F}_{2^{2^3}} $ (with multiplicative group of order 255) consistently, we need to find the smallest number n generating the multiplicative group and satisfying the compatibility condition $n^{17}=4 $. Let’s first concentrate on finding the smallest generator : as 2 is a generator for 1st Fermat-field $\mathbb{F}_{2^{2^1}} $ and 4 a generator for the 2-nd Fermat-field $\mathbb{F}_{2^{2^2}} $ a natural conjecture might be that 16 is a generator for the 3-rd Fermat-field $\mathbb{F}_{2^{2^3}} $ and, more generally, that $2^{2^i} $ would be a generator for the next field $\mathbb{F}_{2^{2^{i+1}}} $.

However, an “exercise” in the 1978-paper by Hendrik Lenstra Nim multiplication asks : “Prove that $2^{2^i} $ is a primitive root in the field $\mathbb{F}_{2^{2^{i+1}}} $ if and only if i=0 or 1.”

I’ve struggled with several of the ‘exercises’ in Lenstra’s paper to the extend I feared Alzheimer was setting in, only to find out, after taking pen and paper and spending a considerable amount of time calculating, that they are indeed merely exercises, when looked at properly… (Spoiler-warning : stop reading now if you want to go through this exercise yourself).

In the picture above I’ve added in red the number $x(x+1)=x^2+1 $ to each of the involutions. Clearly, for each pair these numbers are all distinct and we see that for the indicated pairing they make up all numbers strictly less than 8.

By Conway’s simplicity rules (or by checking) the pair (16,17) gives the number 8. In other words, the equation
$x^2+x+8 $ is an irreducible polynomial over $\mathbb{F}_{16} $ having as its roots in $\mathbb{F}_{256} $ the numbers 16 and 17. But then, 16 and 17 are conjugated under the Galois-involution (the Frobenius $y \mapsto y^{16} $). That is, we have $16^{16}=17 $ and $17^{16}=16 $ and hence $16^{17}=8 $. Now, use the multiplication table in $\mathbb{F}_{16} $ given in the previous post (or compute!) to see that 8 is of order 5 (and NOT a generator). As a consequence, the multiplicative order of 16 is 5×17=85 and so 16 cannot be a generator in $\mathbb{F}_{256} $.
For general i one uses the fact that $2^{2^i} $ and $2^{2^i}+1 $ are the roots of the polynomial $x^2+x+\prod_{j<i} 2^{2^j} $ over $\mathbb{F}_{2^{2^i}} $ and argues as before.

Right, but then what is the minimal generator satisfying $n^{17}=4 $? By computing we see that the pairings of all numbers in the range 16…31 give us all numbers in the range 8…15 and by the above argument this implies that the 17-th powers of all numbers smaller than 32 must be different from 4. But then, the smallest candidate is 32 and one verifies that indeed $32^{17}=4 $ (use the multiplication table given before).

Hence, we must place Knight $K_{32} $ at root $e^{2 \pi i/255} $ and place the other Knights prior to the 256-th at the corresponding power of 32. I forgot the argument I used to find-by-hand the requested place for Knight 16, but one can verify that $32^{171}=16 $ so we seat $K_{16} $ at root $e^{342 \pi i/255} $.

But what about Knight $K_{256} $? Well, by this time I was quite good at squaring and binary representations of integers, but also rather tired, and decided to leave that task to the computer.

If we denote Nim-addition and multiplication by $\oplus $ and $\otimes $, then Conway’s simplicity results in ONAG establish a field-isomorphism between $~(\mathbb{N},\oplus,\otimes) $ and the field $\mathbb{F}_2(x_0,x_1,x_2,\ldots ) $ where the $x_i $ satisfy the Artin-Schreier equations

$x_i^2+x_i+\prod_{j < i} x_j = 0 $

and the i-th Fermat-field $\mathbb{F}_{2^{2^i}} $ corresponds to $\mathbb{F}_2(x_0,x_1,\ldots,x_{i-1}) $. The correspondence between numbers and elements from these fields is given by taking $x_i \mapsto 2^{2^i} $. But then, wecan write every 2-power as a product of the $x_i $ and use the binary representation of numbers to perform all Nim-calculations with numbers in these fields.

Therefore, a quick and dirty way (and by no means the most efficient) to do Nim-calculations in the next Fermat-field consisting of all numbers smaller than 65536, is to use sage and set up the field $\mathbb{F}_2(x_0,x_1,x_2,x_3) $ by

R.< x,y,z,t > =GF(2)[]
S.< a,b,c,d >=R.quotient((x^2+x+1,y^2+y+x,z^2+z+x*y,t^2+t+x*y*z))

To find the smallest number generating the multiplicative group and satisfying the additional compatibility condition $n^{257}=32 $ we have to find the smallest binary number $i_1i_2 \ldots i_{16} $ (larger than 255) satisfying

(i1*a*b*c*t+i2*b*c*t+i3*a*c*t+i4*c*t+i5*a*b*t+i6*b*t+
i7*a*t+i8*t+i9*a*b*c+i10*b*c+i11*a*c+i12*c+i13*a*b+
i14*b+i15*a+i16)^257=a*c

It takes a 2.4GHz 2Gb-RAM MacBook not that long to decide that the requested generator is 1051 (killing another optimistic conjecture that these generators might be 2-powers). So, we seat Knight
$K_{1051} $ at root $e^{2 \pi i/65535} $ and can then arrange seatings for all Knight queued up until we reach the 65536-th! In particular, the first Knight we couldn’t place before, that is Knight $K_{256} $, will be seated at root $e^{65826 \pi i/65535} $.

If you’re lucky enough to own a computer with more RAM, or have the patience to make the search more efficient and get the seating arrangement for the next Fermat-field, please drop a comment.

I’ll leave you with another Lenstra-exercise which shouldn’t be too difficult for you to solve now : “Prove that $x^3=2^{2^i} $ has three solutions in $\mathbb{N} $ for each $i \geq 2 $.”

Comments closed